The Generation of Matlab Symbolic Functions and the Calculation of Its Function Values

I. Introduction
Symbolic function is a very important function of Matlab, which can be used to represent mathematical functions and also perform numerical calculations.There are many ways to create a symbolic function. This paper presents four methods to generate a symbolic function and to find the value of the symbolic function.
Four methods of generating symbolic functions: generating symbolic functions using string expressions, using syms to define symbolic variables to generate symbolic functions, using sym and @ to generate symbolic functions, and using function files to generate symbolic functions.
To find the function value of a symbolic function, you can use the command "matlabFunction" to convert the symbolic function into a representation that can calculate the function value mathematically to calculate the function value of the independent variable at some points.

Second, the generation of symbolic functions
1. The string method
is to write the function expression directly in the string, for example:

y = 'sin(x) - cos(x) + exp(x)'

You can get the running result:

y ='sin(x) - cos(x) + exp(x)'

At this point, the system will automatically identify x as an independent variable.
It should be noted that if some mathematical function symbols provided by the system are used, the argument must be enclosed in a pair of parentheses, otherwise the system will not recognize it (if you have to ask why, you can only answer "thisis the grammar rule of the system")
Note: This method is applicable to matlab7.1 and previous versions, and the new version simply treats it as a string.
2. The syms method (this method is the most commonly used method)
First use the syms command to define the independent variable, and then generate the symbolic function, for example:

syms x;y1 = sin(x) - cos(x) + exp(x)y2 = x^3 + 5*x^2 + 10*x + 1syms x yz = x * exp( -x^2 - y^2 )

Output result:

y1 =exp(x) - cos(x) + sin(x)y2 =x^3 + 5*x^2 + 10*x + 1z =x*exp(- x^2 - y^2)

When derivation of these functions, the system will automatically identify the independent variable. When encountering the derivative of a multivariate function, the default independent variable is the independent variable in the first position.For example

diff( y1 )diff( y2 )diff( z )% derivative function for the default argument xdiff( z, 'x' )% is equivalent to diff( z ), and can also be written as diff( z, x )diff( z, 'y' )% Derivative function for the specified independent variable y

The output is:

ans =3*x^2 + 10*x + 10ans =exp(- x^2 - y^2) - 2*x^2*exp(- x^2 - y^2)ans =exp(- x^2 - y^2) - 2*x^2*exp(- x^2 - y^2)ans =-2*x*y*exp(- x^2 - y^2)

3. Use sym and @ method
First use @ to declare variables, and write symbolic function expressions after them, then you can get symbolic functions.Then use sym to convert it into a symbolic function, and you can perform other symbolic operations, for example:

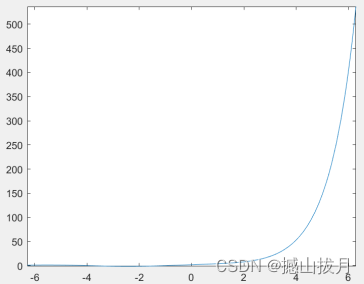
y = @(t)sin(t) - cos(t) + exp(t)ys = sym( y )dy = diff( ys )Idy = int( dy )fplot( y, [ -2*pi, 2*pi ] )figure;fplot( ys, [ -2*pi, 2*pi ] )figure;fplot( dy, [ -2*pi, 2*pi ] )

Output result:

y =function_handle with the following values:@(t)sin(t)-cos(t)+exp(t)ys =exp(t) - cos(t) + sin(t)dy =cos(t) + exp(t) + sin(t)Idy =exp(t) - 2^(1/2)*cos(t + pi/4)

4. The function file method
is to use the function file to generate the symbolic function.For example, the generating function x^n can be implemented as follows:

%xpower.mfunction output=xpower(n)syms xoutput=x^n;

3. Numerical operation of symbolic functions
For symbolic functions, in addition to symbolic operations, it is often necessary to calculate the function values ​​of symbolic functions at certain points.The function value of the symbolic function can be calculated.For example:

clear allclcsyms x;y1 = sin(x) - cos(x) + exp(x);y2 = x^2 - 10*x + 16;y1f = matlabFunction( y1 );y2f = matlabFunction( y2 );x1 = [ 0, pi ];y1v = y1f( x1 )% Calculate the function value of the symbolic function y1f at x1, x1 can be a single coordinate, or an arrayx2 = [ 2 8 ];y2v = y2f( x2 )

Output result:

y1v =0 24.1407y2v =0 0