Matlab符号函数的生成及计算其函数值

一、引言
符号函数是Matlab的一个非常重要的功能，可以用来表示数学上的函数，同时也是进行数值计算。创建符号函数的方法有多种，本文给出了四种生成符号函数的方法及求符号函数函数值的方法。
四种生成符号函数的方法：有利用字符串表达式生成符号函数、利用syms定义符号变量生成符号函数、利用sym和@生成符号函数法、利用函数文件生成符号函数等方法。
求符号函数的函数值，可以使用命令“matlabFunction”来把符号函数转换成可以像数学上计算函数值的表示形式来计算自变量在某些点处的函数值。

二、符号函数的生成
1、字符串法
就是在字符串中直接写函数表达式，例如：

y = 'sin(x) - cos(x) + exp(x)'

则可以得到运行结果：

y =
    'sin(x) - cos(x) + exp(x)'

此时，系统会自动识别x为自变量。
需要注意的是，如果使用了系统提供的一些数学函数符号的话，自变量必须使用一对圆括号括起来，否则系统就不认识了（如果非要问为什么，那只能回答“这是系统的语法规则”）
注意：此法适用于matlab7.1及之前的版本，新版本单纯将其视为字符串。
2、syms法（此法是最常用的方法）
首先利用syms命令定义自变量，然后再生成符号函数，例如：

syms x;
y1 = sin(x) - cos(x) + exp(x)
y2 = x^3 + 5*x^2 + 10*x + 1
syms x y
z = x * exp( -x^2 - y^2 )

输出结果：

y1 =
exp(x) - cos(x) + sin(x)
y2 =
x^3 + 5*x^2 + 10*x + 1
z =
x*exp(- x^2 - y^2)

当对这些函数求导函数时，系统会自动识别自变量，当遇到多元函数求导数时，缺省的自变量就是排在第一个位置的自变量。例如

diff( y1 )
diff( y2 )
diff( z )%对缺省自变量x求导函数
diff( z, 'x' )%等同于diff( z )，也可以写成diff( z, x )
diff( z, 'y' )%对指定的自变量y求导函数

输出结果为：

ans =
3*x^2 + 10*x + 10
ans =
exp(- x^2 - y^2) - 2*x^2*exp(- x^2 - y^2)
ans =
exp(- x^2 - y^2) - 2*x^2*exp(- x^2 - y^2)
ans =
-2*x*y*exp(- x^2 - y^2)

3、利用sym和@法
首先利用@声明变量，在其后写符号函数表达式，此时就可以得到符号函数了。之后使用sym转换成符号函数，就可以进行其它符号运算了，例如：

y = @(t)sin(t) - cos(t) + exp(t)
ys = sym( y )
dy = diff( ys )
Idy = int( dy ) 
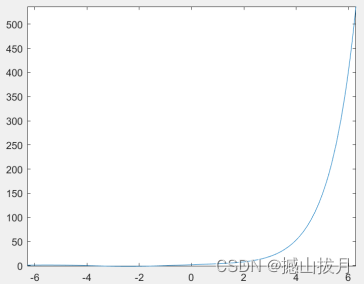
fplot( y, [ -2*pi, 2*pi ] )
figure;
fplot( ys, [ -2*pi, 2*pi ] )
figure;
fplot( dy, [ -2*pi, 2*pi ] )

输出结果：

y =
  包含以下值的 function_handle:
    @(t)sin(t)-cos(t)+exp(t)
ys =
exp(t) - cos(t) + sin(t)
dy =
cos(t) + exp(t) + sin(t)
Idy =
exp(t) - 2^(1/2)*cos(t + pi/4)

4、函数文件法
就是利用函数文件来生成符号函数。例如生成函数x^n，可以如下实现：

%xpower.m
function output=xpower(n)
syms x
output=x^n;

三、符号函数的数值运算
对于符号函数，除了做符号运算之外，往往还需要计算符号函数在某些点处的函数值，此时需要使用matlabFunction命令做一次转换，然后就可以计算该符号函数的函数值了。例如：

clear all
clc
syms x;
y1 = sin(x) - cos(x) + exp(x);
y2 = x^2 - 10*x + 16;
y1f = matlabFunction( y1 );
y2f = matlabFunction( y2 );
x1 = [ 0, pi ];
y1v = y1f( x1 )%计算符号函数y1f在x1的函数值，x1可以是单坐标，也可以说数组
x2 = [ 2 8 ];
y2v = y2f( x2 )

输出结果：

y1v =
     0   24.1407
y2v =
     0     0