中断门，就是通过中断提权的一种手段
下图为中断门的构造

陷阱门也和中断门类似调用什么都类似就是构造不一样

跟调用门类似，但是不能往里面传参，所以高32位的前4位一定为0，同时TYPE位也有细微的改动，其他的并没有太大的改动。

执行流程

直接int 然后根据编号查IDT表，然后IDT表再去查段选择符，然后找到处理的函数，每个编号对应的中断类型都能在官方文档中找到。

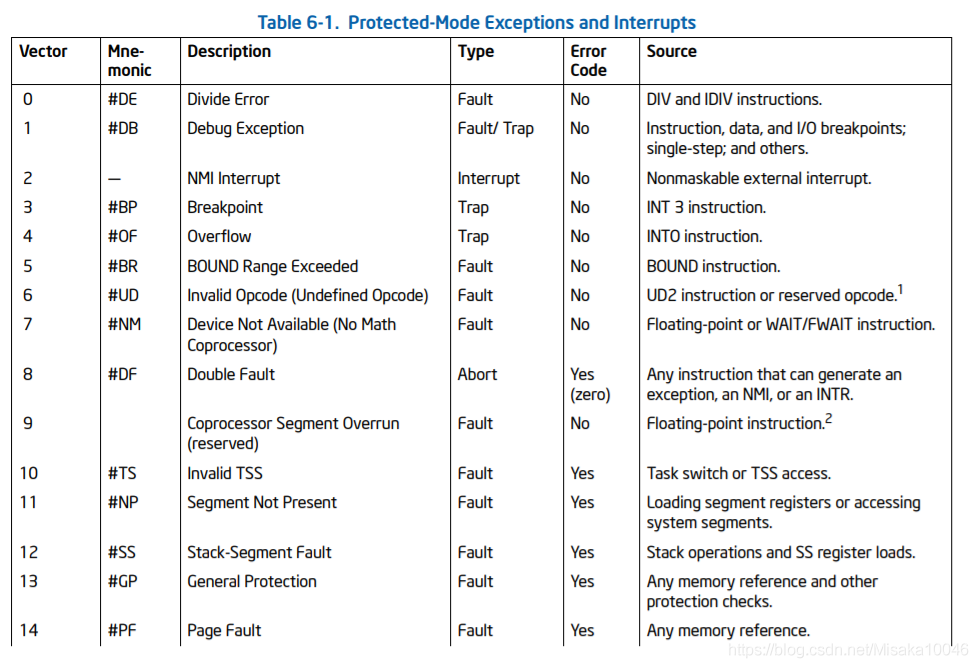
构造过程

最基础的构造

#include "stdafx.h"
#include <WINDOWS.H>

void __declspec(naked) func()
{
    
        __asm{
    
                iretd;
        }
}

int main(void)
{
          
        printf("%x\n",func);
        system("pause");
        __asm{
    
                push fs;
                int 0x20;//通过中断直接调用
                pop fs;
        }
        return 0;
}

可以再执行的前后对比下efl，会发现中断门会把其中的IF位置0，也就是屏蔽可屏蔽中断。
中断门和陷阱门唯一的不同也就是置0的不同，陷阱门不会将IF位置0。

通过中断门来劫持INT 3

#include "stdafx.h"
#include <Windows.h>

typedef int (__cdecl *DbgPrintProc)(_In_z_ _Printf_format_string_ const char * _Format, ...);

DbgPrintProc DbgPrint = (DbgPrintProc)0x83e5f41f;//uf nt!DbgPrint
char *output = "111111";

void __declspec(naked) test()
{
    
	__asm
	{
    
		sub esp,8;
		lea eax, change;
		mov [esp],eax;
		mov [esp+4],0x8;
		jmp fword ptr[esp];//修改CS标志位，不修改的话不会蓝屏，会直接崩系统，原地爆炸
change:
		add esp,8;
		push fs;
		push 0x30;
		pop fs;
		mov eax,[output];
		push eax;
		call DbgPrint;
		add esp, 4;
		pop fs;
		mov eax,0x83e8f5c0;//跳回原来的INT 3中
		jmp eax;
	}
}

void _tmain(int argc, _TCHAR* argv[])
{
    
	printf("%x\r\n",test);
	system("pause");

	__asm
	{
    
		int 3
	};
	system("pause");
}

kd> r gdtr
gdtr=80b95000
kd> dq 80b95000
80b95000  00000000`00000000 00cf9b00`0000ffff
80b95010  00cf9300`0000ffff 00cffb00`0000ffff
80b95020  00cff300`0000ffff 80008b1e`400020ab
80b95030  834093f7`bc003748 0040f300`00000fff
80b95040  0000f200`0400ffff 7ccf9b57`1a40ffff
80b95050  830089f7`90000068 830089f7`90680068
80b95060  00000000`00000000 00000000`00000000
80b95070  800092b9`500003ff 00000000`00000000
kd> r idtr
idtr=80b95400
kd> dq 80b95400
80b95400  83e88e00`0008efc0 83e88e00`008f150
80b95410  83e8ee00`0048f5c0 83e8ee00`0008f5c0
80b95420  83e8ee00`0008f748 83e88e00`0008f8a8
80b95430  83e88e00`0008fa1c 83e98e00`00080018
80b95440  00008500`00500000 83e98e00`00080478
80b95450  83e98e00`0008059c 83e98e00`000806dc
80b95460  83e98e00`0008093c 83e98e00`00080c2c
80b95470  83e98e00`000812fc 83e98e00`000816b0
kd> eq 80b95418 83e8ee00`0048f5c0

这里修改的是INT 3中的段选择子，而段选择子是决定代码开始地址的地方，因此我们修改段选择子指向GDT表中的第10项，再GDT表项中创建第10项，然后第10项大部分复制第2项，只修改其中的基地址，修改为test函数地址减去INT 3中断的代码起始地址，这样基地址根据偏移就会直接去执行我们的test函数，然后再去执行INT 3。

然后实验成功。PS：后面跟了一串不知道啥。不用去管他。

TIPS

在中断门内部调用代码的时候，需要使用CLI/STI来屏蔽中断，不进行屏蔽的话，可能在切换进程的时候蓝屏。