相机成像+单应性变换+相机标定+立体校正

1.相机模型

参考：智能机器人目标抓取关键技术研究–谢心如 哈尔滨工程大学 博士论文
小孔成像，直接上图：

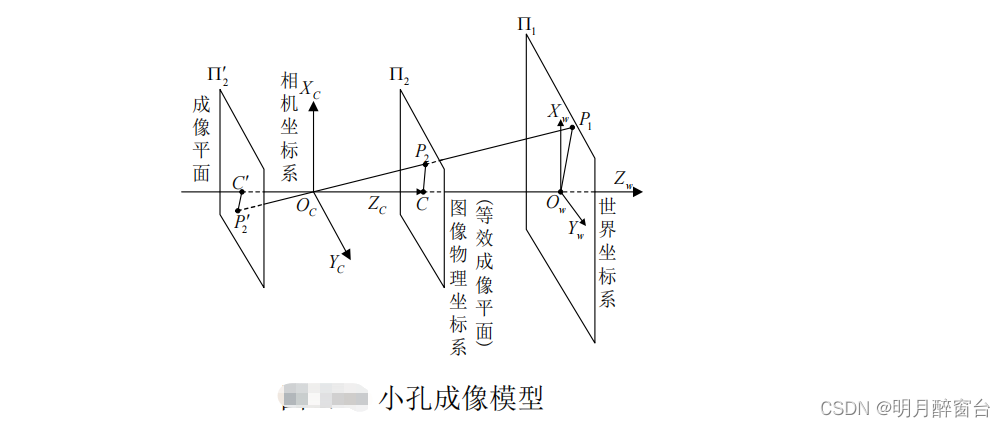
建立相机坐标系和图像像素坐标系来描述空间坐标和图像坐标的关系。相机坐标系以相机的光轴中心点为原点，以光轴方向为 Z 轴，图像的像素坐标用二维坐标表示，成像平面与光轴交点对应的图像坐标记为(u0,v0) 。
在相机坐标系下，空间中的点 P和对应的图像像素坐标(u，v) 之间的关系为：


理想的小孔模型中不考虑相机镜头的畸变，实际上由于制造和组装原因，相机镜头
在成像时产生畸变。常用的畸变模型为 Brown 模型，考虑了径向畸变和切向畸变，

最后用一幅图来总结从世界坐标系到像素坐标系（不考虑畸变）的转换关系：

2.单应性矩阵

单应性变换（Homography）变换，描述物体在世界坐标系和像素坐标系之间的位置映射关系，单应性矩阵定义为：

其中，M是相机内参矩阵

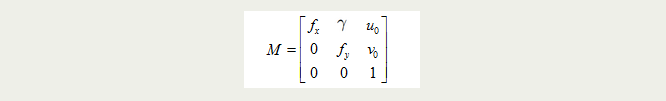
单应性在计算机视觉领域是一个非常重要的概念，它在图像校正、图像拼接、相机位姿估计、视觉SLAM等领域有非常重要的作用。

如何根据标定图得到单应性矩阵？
1、打印一张棋盘格标定图纸，将其贴在平面物体的表面。
2、拍摄一组不同方向棋盘格的图片，可以通过移动相机来实现，也可以移动标定图片来实现。
3、对于每张拍摄的棋盘图片，检测图片中所有棋盘格的特征点（角点，也就是下图中黑白棋盘交叉点，中间品红色的圆圈内就是一个角点）。我们定义打印的棋盘图纸位于世界坐标系Zw=0的平面上，世界坐标系的原点位于棋盘图纸的固定一角（比如下图中黄色点）。像素坐标系原点位于图片左上角。

4、因为棋盘标定图纸中所有角点的空间坐标是已知的，这些角点对应在拍摄的标定图片中的角点的像素坐标也是已知的，如果我们得到这样的N>=4个匹配点对（越多计算结果越鲁棒），就可以根据LM等优化方法得到其单应矩阵H。当然计算单应矩阵一般不需要自己写函数实现，OpenCV中就有现成的函数可以调用，对应的c++函数是:

Mat findHomography(InputArray srcPoints, InputArray dstPoints, int method=0, 
double ransacReprojThreshold=3, OutputArray mask=noArray() )

从函数定义来看，只要输入匹配点对，指定具体计算方法即可输出结果。

具体推到原理可详见（+参考）从零开始学习「张氏相机标定法」-- 计算机视觉life

3.相机标定

典型：张正友-棋盘格标定法




注:机械臂手眼标定参考论文第2章

Opencv标定过程及API介绍

opencv双目相机标定-示例代码分析：https://blog.csdn.net/qq_15751687/article/details/117886678

4.极线校正

极线校正，有的称为立体校正，正常相机标定过程应为以下流程：

1.相机标定得到内参、外参
2.畸变校正
3.立体校正(极线校正)

具体原理详见：
原理+代码实战 | 双目视觉中的极线校正：https://blog.csdn.net/qq_42722197/article/details/118663803

opencv实现极线校正过程：
opencv 双目标定操作完整版：https://blog.csdn.net/hejingkui/article/details/80488763

参考论文复现立体校正算法以便实现三维重建：

论文：A Compact Algorithm for Rectification of Stereo Pairs
参考：一种简洁的双目校正算法–A Compact Algorithm for Rectification of Stereo Pairs

附

4.1.matlab实现

function [T1,T2,Pn1,Pn2] = rectify(Po1,Po2)
% RECTIFY: compute rectification matrices
% factorize old PPMs
[A1,R1,t1] = art(Po1);
[A2,R2,t2] = art(Po2);
% optical centers (unchanged)
c1 = - inv(Po1(:,1:3))*Po1(:,4);
c2 = - inv(Po2(:,1:3))*Po2(:,4);
% new x axis (= direction of the baseline)
v1 = (c1-c2);
% new y axes (orthogonal to new x and old z)
v2 = cross(R1(3,:)’,v1);
% new z axes (orthogonal to baseline and y)
v3 = cross(v1,v2);
% new extrinsic parameters
R = [v1’/norm(v1)
v2’/norm(v2)
v3’/norm(v3)];
% translation is left unchanged
% new intrinsic parameters (arbitrary)
A = (A1 + A2)./2;
A(1,2)=0; % no skew
% new projection matrices
Pn1 = A * [R -R*c1 ];
Pn2 = A * [R -R*c2 ];
% rectifying image transformation
T1 = Pn1(1:3,1:3)* inv(Po1(1:3,1:3));
T2 = Pn2(1:3,1:3)* inv(Po2(1:3,1:3));

% ------------------------
function [A,R,t] = art(P)
% ART: factorize a PPM as P=A*[R;t]

Q = inv(P(1:3, 1:3));
[U,B] = qr(Q);

R = inv(U);
t = B*P(1:3,4);
A = inv(B);
A = A ./A(3,3);

4.2.C++实现参考

极线校正方法的原理及C++实现：https://www.freesion.com/article/7403499712/

C++实现qr分解：将投影矩阵P分解为A(本质矩阵)，R(旋转矩阵)，T(平移矩阵)