当前位置:网站首页>Prefix sum of integral function -- Du Jiao sieve
Prefix sum of integral function -- Du Jiao sieve
2022-04-23 09:43:00 【Zimba_】
background :
This class is so boring , Too noisy to learn , Just write a blog .
subject :
Given a n n n, seek ∑ i = 1 n μ ( i ) \sum_{i=1}^{n}\mu(i) ∑i=1nμ(i) and ∑ i = 1 n φ ( i ) \sum_{i=1}^{n}\varphi(i) ∑i=1nφ(i).
( 1 ≤ n ≤ 1 0 10 ) (1\leq n\leq 10^{10}) (1≤n≤1010)
( Prefixes and of some integrable functions )
introduction :
If you don't know what an integral function is, go out and turn left Next door classroom .
We know , μ \mu μ Functions and φ \varphi φ Sure o ( n ) o(\sqrt{n}) o(n) Find the value of a single point .
You can also use a linear sieve o ( n ) o(n) o(n) Preprocess the values of multiple points .
But obviously it's not enough for this problem .
Come to such a magical place , These integrable functions have a sub linear algorithm to find the prefix and , Maybe this is the charm of Mathematics .
Here we introduce one of the methods , Dujiao sieve , It can be o ( n 3 4 ) o(n^{\frac{3}{4}}) o(n43) Find the prefix and sum of the integral function within the complexity of . And we can preprocess it out before 1 0 6 10^6 106 Two prefixes and , Optimize its complexity to o ( n 2 3 ) o(n^{\frac{2}{3}}) o(n32).
Text : Dujiao sieve
Suppose that the function we require the prefix and is f f f, And make its prefix and S ( n ) = ∑ i = 1 n f ( i ) S(n)=\sum_{i=1}^{n}f(i) S(n)=∑i=1nf(i).
Let's find another function g g g Convolute with it to find the prefix sum .
∑ i = 1 n ( f ∗ g ) ( i ) = ∑ i = 1 n ∑ d ∣ i g ( d ) f ( i d ) \sum_{i=1}^{n}(f*g)(i)=\sum_{i=1}^{n}\sum_{d|i}g(d)f(\frac{i}{d}) ∑i=1n(f∗g)(i)=∑i=1n∑d∣ig(d)f(di)
= ∑ d = 1 n g ( d ) ∑ i = 1 ⌊ n d ⌋ f ( i ) =\sum_{d=1}^{n}g(d)\sum_{i=1}^{\lfloor \frac{n}{d} \rfloor}f(i) =∑d=1ng(d)∑i=1⌊dn⌋f(i)
= ∑ d = 1 n g ( d ) S ( ⌊ n d ⌋ ) =\sum_{d=1}^{n}g(d)S(\lfloor \frac{n}{d} \rfloor) =∑d=1ng(d)S(⌊dn⌋)
Push it here , We find that this is an obvious number theory block formula .
But there is no in this formula S ( n ) S(n) S(n) ah , no S ( n ) S(n) S(n) What are we asking for .
So now we're going to S ( n ) S(n) S(n) Get it out .
We found that when d = 1 d=1 d=1 when , This thing in the back g ( 1 ) S ( ⌊ n 1 ⌋ ) = S ( n ) g(1)S(\lfloor \frac{n}{1} \rfloor)=S(n) g(1)S(⌊1n⌋)=S(n)
then S ( n ) S(n) S(n) came .
S ( n ) = ∑ d = 1 n g ( d ) S ( ⌊ n d ⌋ ) − ∑ d = 2 n g ( d ) S ( ⌊ n d ⌋ ) S(n)=\sum_{d=1}^{n}g(d)S(\lfloor \frac{n}{d} \rfloor)-\sum_{d=2}^{n}g(d)S(\lfloor \frac{n}{d} \rfloor) S(n)=∑d=1ng(d)S(⌊dn⌋)−∑d=2ng(d)S(⌊dn⌋)
= ∑ i = 1 n ( f ∗ g ) ( i ) − ∑ d = 2 n g ( d ) S ( ⌊ n d ⌋ ) =\sum_{i=1}^{n}(f*g)(i)-\sum_{d=2}^{n}g(d)S(\lfloor \frac{n}{d} \rfloor) =∑i=1n(f∗g)(i)−∑d=2ng(d)S(⌊dn⌋)
Then the latter formula is still a number theory block formula , As long as we can quickly find g g g And , You can quickly find out .
So we need to find one g g g, bring g g g and f ∗ g f*g f∗g The prefix and are easy to find .
Let's now calculate the complexity , hypothesis g g g and f ∗ g f*g f∗g The prefix and can o ( 1 ) o(1) o(1) Find out . Excuse me , Anyway, the complexity is o ( n 3 4 ) o(n^{\frac{3}{4}}) o(n43), If we preprocess out before 1 0 6 10^6 106 term , Then add a memory , Complexity becomes o ( n 2 3 ) o(n^{\frac{2}{3}}) o(n32) 了 .
So there are .
The code is omitted , Please write your own questions .
Example 1: seek ∑ i = 1 n μ ( i ) \sum_{i=1}^{n}\mu(i) ∑i=1nμ(i).
When we consider solving the prefix sum of integral functions with Duchenne sieve , The main thing is to find one g g g bring g g g and f ∗ g f*g f∗g Prefix and easy to find .
So for the Mobius function μ \mu μ, There is no doubt that we choose to use 1 1 1 function .
Yes μ ∗ 1 = e \mu *1=e μ∗1=e.
that 1 1 1 Functions and e e e There is no need to say more about the prefix and sum of functions .
The reason is A.
Example 2: seek ∑ i = 1 n φ ( i ) \sum_{i=1}^{n}\varphi(i) ∑i=1nφ(i).
g g g Still choose to use 1 1 1 function , Yes φ ∗ 1 = i d \varphi *1=id φ∗1=id.
that 1 1 1 Functions and i d id id The prefix summation function is also very good .
Example 3: seek ∑ i = 1 n i φ ( i ) \sum_{i=1}^{n}i\varphi(i) ∑i=1niφ(i).
We chose to use i d id id As g g g function , First i d id id The prefix and sum of functions can be found .
∑ i = 1 n ( f ∗ i d ) ( i ) = ∑ i = 1 n ∑ d ∣ i d φ ( d ) ∗ i d = ∑ i = 1 n i ∑ d ∣ i φ ( d ) = ∑ i = 1 n i 2 \sum_{i=1}^{n}(f*id)(i)=\sum_{i=1}^{n}\sum_{d|i}d\varphi(d)*\frac{i}{d}=\sum_{i=1}^{n}i\sum_{d|i}\varphi(d)=\sum_{i=1}^{n}i^{2} ∑i=1n(f∗id)(i)=∑i=1n∑d∣idφ(d)∗di=∑i=1ni∑d∣iφ(d)=∑i=1ni2.
among , because 1 ∗ φ = i d 1*\varphi =id 1∗φ=id, therefore ∑ d ∣ i φ ( d ) = i \sum_{d|i}\varphi(d)=i ∑d∣iφ(d)=i.
Example n+2: seek ∑ i = 1 n i n φ ( i ) \sum_{i=1}^{n}i^{n}\varphi(i) ∑i=1ninφ(i).
We chose to use i d n id^{n} idn As g g g function , that i d n id^{n} idn The prefix and sum of can be found .( Lagrange interpolation ?)
∑ i = 1 n ( f ∗ i d ) ( i ) = ∑ i = 1 n ∑ d ∣ i d n φ ( d ) ∗ ( i d ) n = ∑ i = 1 n i n ∑ d ∣ i φ ( d ) = ∑ i = 1 n i n + 1 \sum_{i=1}^{n}(f*id)(i)=\sum_{i=1}^{n}\sum_{d|i}d^{n}\varphi(d)*(\frac{i}{d})^{n}=\sum_{i=1}^{n}i^{n}\sum_{d|i}\varphi(d)=\sum_{i=1}^{n}i^{n+1} ∑i=1n(f∗id)(i)=∑i=1n∑d∣idnφ(d)∗(di)n=∑i=1nin∑d∣iφ(d)=∑i=1nin+1.
For the time being, I know that's all above .
版权声明
本文为[Zimba_]所创,转载请带上原文链接,感谢
https://yzsam.com/2022/04/202204230621424922.html
边栏推荐
- Go language learning notes - structure | go language from scratch
- Flink 流批一体在小米的实践
- 《數字電子技術基礎》3.1 門電路概述、3.2 半導體二極管門電路
- Example of data object mask used by SAP translate
- Codeforces Round #784 (Div. 4)
- Using JS to realize a thousandth bit
- 云身份过于宽松,为攻击者打开了大门
- MySQL of database -- overview and installation
- Using sqlmap injection to obtain the account and password of the website administrator
- Code source daily question div1 (701-707)
猜你喜欢

JS DOM event
![3、 6 [Verilog HDL] gate level modeling of basic knowledge](/img/36/46f2413ecb12f81c003848c93f6bc9.jpg)
3、 6 [Verilog HDL] gate level modeling of basic knowledge
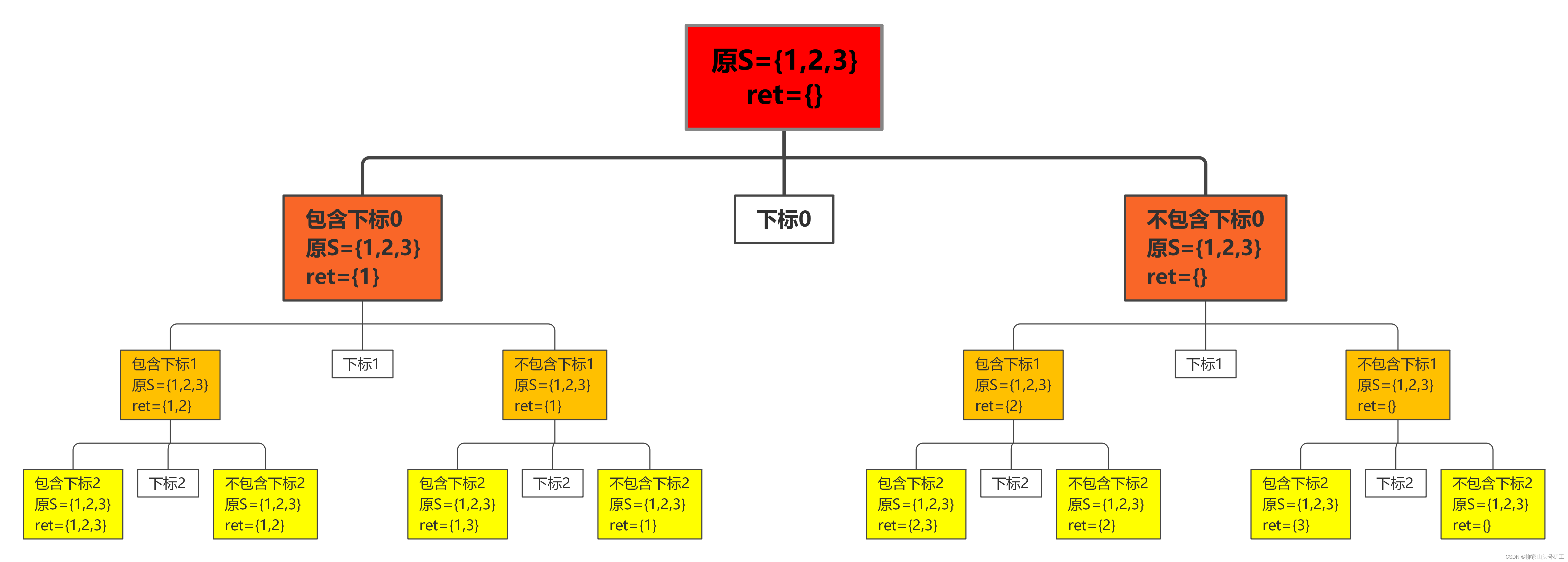
Leetcode question bank 78 Subset (recursive C implementation)
Canary publishing using ingress

Go language learning notes - array | go language from scratch

Installation of data cleaning ETL tool kettle
Kettle experiment conversion case
![[reading notes] Chapter 5 conditional statements, circular statements and block statements of Verilog digital system design tutorial (with answers to thinking questions)](/img/a2/b50fadad859a050eecfa15a436e126.png)
[reading notes] Chapter 5 conditional statements, circular statements and block statements of Verilog digital system design tutorial (with answers to thinking questions)
![Sql1 [geek challenge 2019]](/img/ad/afca09bc1da003393319af700e90e3.png)
Sql1 [geek challenge 2019]

High paid programmer & interview question series 91 limit 20000 loading is very slow. How to solve it? How to locate slow SQL?
随机推荐
Kettle experiment (III)
How to obtain geographical location based on photos and how to prevent photos from leaking geographical location
高薪程序员&面试题精讲系列91之Limit 20000加载很慢怎么解决?如何定位慢SQL?
kettle庖丁解牛第14篇之JSON输入
DVWA range practice record
Kettle experiment
Give the method of instantiating the object to the new object
Leetcode题库78. 子集(递归 c实现)
Number of islands
SAP salv14 background output salv data can directly save files and send emails (with sorting, hyperlink and filtering format)
Leetcode0587. Install fence
阿里云架构师解读四大主流游戏架构
理解作用域
Redis exception read error on connection solution
MySQL of database -- overview and installation
Setnx command execution failed due to full redis memory
Single sign on SSO
Vivo, hardware safe love and thunder
JS and how to judge custom attributes in H5
Number theory blocking (integer division blocking)