当前位置:网站首页>基于TensorFlow的线性回归实例
基于TensorFlow的线性回归实例
2022-04-23 05:50:00 【Stephen_Tao】
文章目录
线性回归原理
- 根据训练数据建立回归模型 y = w 1 x 1 + w 2 x 2 + . . . + w n x n + b y=w_1x_1+w_2x_2+...+w_nx_n+b y=w1x1+w2x2+...+wnxn+b
- 建立预测值与真实值间的误差损失函数
- 采用梯度下降法优化误差损失函数,对最优的权重和偏置进行预测
实例分析
1. 训练数据生成
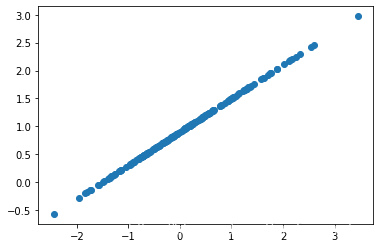
- 随机生成200个服从正态分布的数据点
- 数据本身分布为 y = 0.6 x + 0.9 y=0.6x+0.9 y=0.6x+0.9
随机数据点可视化代码如下:
import tensorflow as tf
import matplotlib.pyplot as plt
X = tf.random.normal(shape=(200, 1), mean=0, stddev=1)
y_true = tf.matmul(X, [[0.6]]) + 0.9
plt.scatter(X,y_true)
plt.show()
2. 建立线性回归模型
采用TensorFlow建立线性回归模型,代码如下:
def Linear_regression():
with tf.compat.v1.Session() as sess:
# 生成正态分布的随机数据
X = tf.random.normal(shape=(200, 1), mean=0, stddev=1)
y_true = tf.matmul(X, [[0.6]]) + 0.9
# 初始化线性回归的权重和偏置
weight = tf.Variable(initial_value=tf.random.normal(shape=(1, 1)))
bias = tf.Variable(initial_value=tf.random.normal(shape=(1, 1)))
# 采用初始化参数建立线性回归模型
y_predict = tf.matmul(X, weight) + bias
# 建立误差损失函数
error = tf.reduce_mean(tf.square(y_predict - y_true))
# 采用随机梯度下降法进行模型训练
optimizer = tf.compat.v1.train.GradientDescentOptimizer(learning_rate=0.05).minimize(error)
# 初始化会话中的变量
init = tf.compat.v1.global_variables_initializer()
sess.run(init)
# 记录每次训练得到的损失值
error_set = []
# 训练200次,打印每次训练的权重、偏置及损失
for i in range(200):
sess.run(optimizer)
error_set.append(error.eval())
print("第%d步的误差为%f,权重为%f,偏置为%f" %(i,error.eval(),weight.eval(),bias.eval()))
运行结果如下:
第0步的误差为0.869870,权重为1.532328,偏置为0.675902
第1步的误差为0.663277,权重为1.428975,偏置为0.691342
第2步的误差为0.637269,权重为1.346699,偏置为0.713041
第3步的误差为0.434829,权重为1.280713,偏置为0.727712
第4步的误差为0.456109,权重为1.209046,偏置为0.745070
第5步的误差为0.276588,权重为1.146608,偏置为0.758473
第6步的误差为0.268131,权重为1.080588,偏置为0.770594
第7步的误差为0.201195,权重为1.024212,偏置为0.794897
第8步的误差为0.136823,权重为0.988268,偏置为0.804994
第9步的误差为0.123242,权重为0.950725,偏置为0.811171
第10步的误差为0.131416,权重为0.922447,偏置为0.819484
第11步的误差为0.084628,权重为0.897494,偏置为0.826534
第12步的误差为0.072482,权重为0.873246,偏置为0.833084
第13步的误差为0.073851,权重为0.841141,偏置为0.842617
第14步的误差为0.046367,权重为0.811977,偏置为0.849992
第15步的误差为0.034317,权重为0.789964,偏置为0.855224
第16步的误差为0.026889,权重为0.767914,偏置为0.861630
第17步的误差为0.020377,权重为0.751666,偏置为0.866115
第18步的误差为0.020895,权重为0.735054,偏置为0.871480
第19步的误差为0.016006,权重为0.718687,偏置为0.872991
第20步的误差为0.012947,权重为0.707634,偏置为0.875760
第21步的误差为0.011159,权重为0.698776,偏置为0.878277
第22步的误差为0.008542,权重为0.688199,偏置为0.881770
第23步的误差为0.006672,权重为0.679353,偏置为0.884191
第24步的误差为0.005545,权重为0.671653,偏置为0.885150
第25步的误差为0.003817,权重为0.664658,偏置为0.885894
第26步的误差为0.003786,权重为0.658720,偏置为0.886094
第27步的误差为0.002937,权重为0.652663,偏置为0.887146
第28步的误差为0.002135,权重为0.646956,偏置为0.888744
第29步的误差为0.001883,权重为0.641135,偏置为0.890537
第30步的误差为0.001530,权重为0.637612,偏置为0.891546
第31步的误差为0.001205,权重为0.633786,偏置为0.892773
第32步的误差为0.000896,权重为0.630734,偏置为0.892999
第33步的误差为0.000742,权重为0.627161,偏置为0.893859
第34步的误差为0.000600,权重为0.624422,偏置为0.894859
第35步的误差为0.000556,权重为0.622399,偏置为0.895277
第36步的误差为0.000471,权重为0.620324,偏置为0.895607
第37步的误差为0.000341,权重为0.618261,偏置为0.895853
第38步的误差为0.000309,权重为0.616247,偏置为0.896142
第39步的误差为0.000233,权重为0.614667,偏置为0.896652
第40步的误差为0.000219,权重为0.613210,偏置为0.896935
...
第194步的误差为0.000000,权重为0.600000,偏置为0.900000
第195步的误差为0.000000,权重为0.600000,偏置为0.900000
第196步的误差为0.000000,权重为0.600000,偏置为0.900000
第197步的误差为0.000000,权重为0.600000,偏置为0.900000
第198步的误差为0.000000,权重为0.600000,偏置为0.900000
第199步的误差为0.000000,权重为0.600000,偏置为0.900000
训练过程中损失值变化折线图如下:
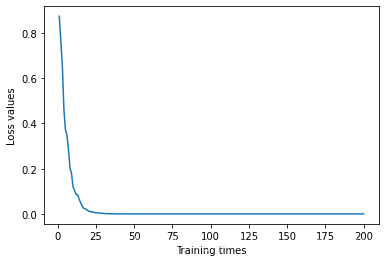
可以看到随着训练次数的增加,损失函数的值逐渐减小,最后变为0。训练过程中所预测的最优参数也与实际的数据分布参数相符。
小结
本文介绍了线性回归的基本原理与步骤,并基于TensorFlow实现了简单的线性回归任务,取得了良好的效果。
版权声明
本文为[Stephen_Tao]所创,转载请带上原文链接,感谢
https://blog.csdn.net/professor_tao/article/details/119292134
边栏推荐
猜你喜欢
Graduation project, viewing screenshots of epidemic psychological counseling system

搭建jpress个人博客

Introduction to nonparametric camera distortion model

C语言实用小技巧合集(持续更新)
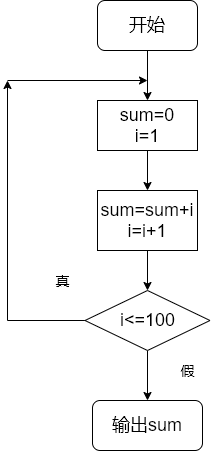
C语言循环结构程序

类的继承与派生

【UDS统一诊断服务】一、诊断概述(1)— 诊断概述

Cross domain issues - allow origin header contains multiple values but only one is allowed
【UDS统一诊断服务】(补充)五、ECU bootloader开发要点详解 (2)

C语言的浪漫
随机推荐
【OpenCV】使用 FileStorage 读写 Eigen 向量
P1018 maximum product solution
The waterfall waterfall flow of uview realizes single column and loads more
ArcGIS license错误-15解决方法
【UDS统一诊断服务】一、诊断概述(1)— 诊断概述
Vscode custom comments
gst-launch-1.0用法小记
PM2 deploy nuxt related commands
ArcGIS表转EXCEL超出上限转换失败
日志
识别验证码
Uniapp encapsulates request
圆整 round 的一点点小细节
使用TransmittableThreadLocal实现参数跨线程传递
拷贝构造函数
如何安装jsonpath包
安全授信
[UDS] unified diagnostic service (UDS)
爬虫效率提升方法
Robocode教程7——雷达锁定