当前位置:网站首页>[CF 1425D]Danger of Mad Snakes(组合计数+容斥)
[CF 1425D]Danger of Mad Snakes(组合计数+容斥)
2022-04-23 06:21:00 【Zimba_】
题意:
有一个 1000 × 1000 1000\times 1000 1000×1000的方格。有 n n n条蛇在方格中,每条蛇告诉你在方格中的坐标 ( X i , Y i ) (X_{i},Y_{i}) (Xi,Yi)和一个权值 B i B_{i} Bi。
然后任意选其中 m m m条蛇,对于每条被选中的蛇,它和所有满足 m a x ( ∣ X ′ − X ∣ , ∣ Y ′ − Y ∣ ) < = R max(|X'-X|,|Y'-Y|)<=R max(∣X′−X∣,∣Y′−Y∣)<=R的位于 ( X ′ , Y ′ ) (X',Y') (X′,Y′)的蛇都会被杀死。
对于其中一次选法,它的权值是所有在该选法中被杀死的蛇的权值和的平方。
求所有选法的权值总和。
思路:
考虑权值和的平方 ( B i + B j + B k ) 2 (B_{i}+B_{j}+B_{k})^{2} (Bi+Bj+Bk)2,我们把平方式拆开变成 B i 2 + B j 2 + B k 2 + 2 B i B j + 2 B i B k + 2 B j B k B_{i}^{2}+B_{j}^{2}+B_{k}^{2}+2B_{i}B_{j}+2B_{i}B_{k}+2B_{j}B_{k} Bi2+Bj2+Bk2+2BiBj+2BiBk+2BjBk。
考虑计算单个平方项 B i 2 B_{i}^{2} Bi2的贡献,就是每条蛇被选取的总次数 × B i 2 \times B_{i}^{2} ×Bi2。
我们计算一下 情况总数 − - −没有被选到的情况数 就行了。
考虑计算两项相乘项 2 B i B j 2B_{i}B_{j} 2BiBj的贡献,就是两条蛇都被选取的次数 × 2 B i B j \times 2B_{i}B_{j} ×2BiBj。
这个我们容斥一下,计算 两条都不被选取的情况数+ i i i被选取的情况数+ j j j被选取的情况数-总情况数 就行了。
代码:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod = 1000000007;
ll fpow(ll a,ll n)
{
ll sum=1,base=a%mod;
while(n!=0)
{
if(n%2)sum=sum*base%mod;
base=base*base%mod;
n/=2;
}
return sum;
}
ll inv(ll a)
{
return fpow(a,mod-2);
}
ll jie[1000005],rjie[1000005];
void initJie(ll n)
{
jie[0]=1;
for(ll i=1;i<=n;i++)jie[i]=jie[i-1]*i%mod;
for(ll i=0;i<=n;i++)rjie[i]=inv(jie[i]);
}
ll C(ll n,ll k)
{
if(k>n)return 0;
else return jie[n]*rjie[k]%mod*rjie[n-k]%mod;
}
ll n,m,r;
ll x[2005],y[2005],b[2005];
bitset<2005>num[2005],tmp;
ll get1(ll i)
{
return (b[i]*b[i]%mod*(C(n,m)-C(n-num[i].count(),m))%mod+mod)%mod;
}
ll get2(ll i,ll j)
{
tmp=num[i]|num[j];
return 2*b[i]*b[j]%mod*(C(n-tmp.count(),m)+(C(n,m)-C(n-num[i].count(),m))-C(n-num[j].count(),m))%mod;
}
int main()
{
initJie(100000);
scanf("%lld%lld%lld",&n,&m,&r);
for(ll i=1;i<=n;i++)
{
scanf("%lld%lld%lld",&x[i],&y[i],&b[i]);
}
for(ll i=1;i<=n;i++)
{
for(ll j=1;j<=n;j++)
{
if(max(abs(x[j]-x[i]),abs(y[j]-y[i]))<=r)
{
num[i].set(j);
}
}
}
ll ans=0;
for(ll i=1;i<=n;i++)
{
ans=(ans+get1(i))%mod;
}
for(ll i=1;i<=n;i++)
{
for(ll j=i+1;j<=n;j++)
{
ans=(ans+get2(i,j))%mod;
}
}
printf("%lld\n",(ans%mod+mod)%mod);
return 0;
}
版权声明
本文为[Zimba_]所创,转载请带上原文链接,感谢
https://blog.csdn.net/weixin_43785386/article/details/109048515
边栏推荐
- null和undefined的区别
- van-uploader上传图片实现过程、使用原生input实现上传图片
- Hanlp分词器(通过spark)
- PyTorch 22. Pytorch common code snippet collection
- remote: Support for password authentication was removed on August 13, 2021.
- Emergency communication system for flood control and disaster relief
- 可视化常见问题解决方案(七)画图刻度设置解决方案
- The difference between null and undefined
- 可视化常见绘图(一)堆叠图
- 组合数求解与(扩展)卢卡斯定理
猜你喜欢

可视化之路(十二)Collection类详解
Meishe technology launches professional video editing solution for desktop -- Meiying PC version

自定义钉钉机器人进行报警

地铁无线对讲系统

Machine vision series (02) -- tensorflow2 3 + win10 + GPU installation

Lead the industry trend with intelligent production! American camera intelligent video production platform unveiled at 2021 world Ultra HD Video Industry Development Conference

DMR system solution of Kaiyuan MINGTING hotel of Fengqiao University

Tensorflow安装后ImportError: DLL load failed: 找不到指定的模块,且国内安装缓慢
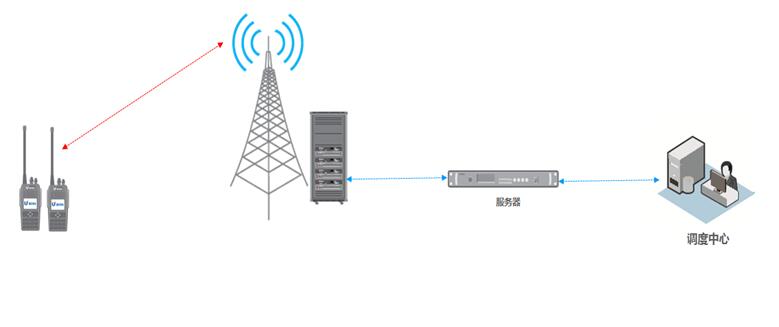
海南凤凰机场智能通信解决方案

不需要破解markdown编辑工具Typora
随机推荐
Emergency medical communication solution | mesh wireless ad hoc network system
Transformer的pytorch实现
How does the public and Private Integrated walkie talkie realize cooperative work under multi-mode communication?
PyTorch 19. Differences and relations of similar operations in pytorch
Lead the industry trend with intelligent production! American camera intelligent video production platform unveiled at 2021 world Ultra HD Video Industry Development Conference
自组网灵活补盲|北峰油气田勘测解决方案
海南凤凰机场智能通信解决方案
地铁无线对讲系统
PyTorch 10. Learning rate
免费开源农业物联网云平台(Version:3.0.1)
Jupyter Notebook 安装
南方投资大厦SDC智能通信巡更管理系统
记录一个查询兼容性的网站,String.replaceAll()兼容性报错
Take you to travel in space, and American photography technology provides comprehensive technical support for aerospace creative applet
简单易懂的子集dp
PyTorch 17. GPU concurrency
按需引入vant组件
presto日期函数的使用
C语言的指针符号到底靠近变量类型还是变量名?
Meishe technology launches professional video editing solution for desktop -- Meiying PC version