当前位置:网站首页>c语言函数的递归调用(汉诺塔问题,楼梯递归问题等)
c语言函数的递归调用(汉诺塔问题,楼梯递归问题等)
2022-08-09 10:48:00 【Cutecumber】
c语言函数的递归调用(汉诺塔Hanoi问题,楼梯递归问题等)
刚接触c语言的时候,感觉函数递归调用这里比较绕,难以理解,现在本着复习的目的,捋顺一下,介绍几个递归的题目。
1.什么是递归调用
函数的递归调用是指在调用一个函数的过程中直接或间接调用该函数本身。
2.重点分析
重点在于分析要解决的某个问题前n-1次和第n次过程存在的递归关系;再者,递归的起始条件的不要忽略,应单独写出。
3.举例说明
3.1 递归求n!
分析:n!=n*(n-1)!; (n-1)!=(n-1)*(n-2)!……当n=1时,n!=1.
函数代码:
int jiecheng(int n)
{
if(n==1)
return 1;
else
return(n*jiecheng(n-1));
}
3.2 汉诺(Hanoi)塔问题
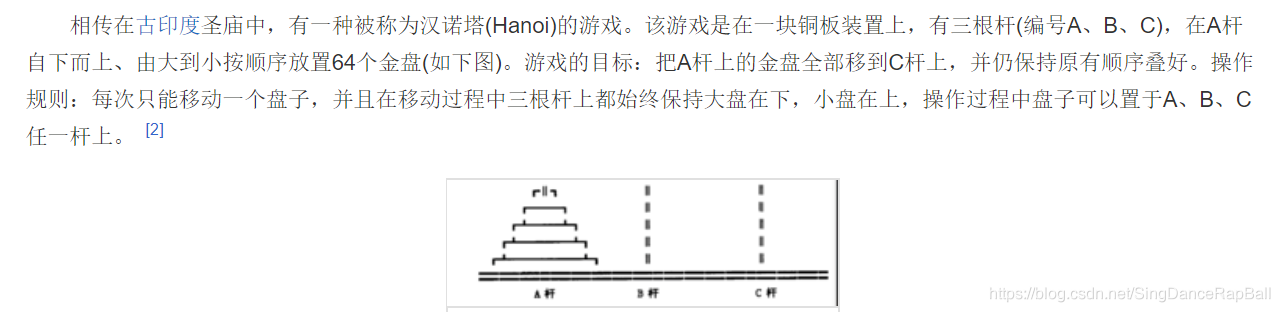
分析:搞懂前n-1次和最后1次怎么移动,当n=1时这种特例也要单独考虑。
以n=64为例,考虑的解题步骤应该是:假设有个高手能把前63层从A移动到B(大在下小在上的顺序)且不管他是怎么移动的,我们需要做的是将A的最后一层移动到C,再将B的63层移到C,这样就完成了最后一步。
往前递推:这个高手把前63层从A移动到B,从B移到C也要用上述做法完成,如下图
最终递归至n=1.
当n=1时,只需将这一层从A->C.
函数代码:
void hanoi(int n, char A, char B, char C) //实现n层塔从A借助B移动到C。
{
void move(char a, char b);
if(n==1)
move(A, C);
else
{
hanoi(n-1, A, C, B); //前n-1层从A借助C移动到B
move(A, C); //第n层从A移到C
hanoi(n-1, B, A, C); //移动到B的n-1层借助A移动到C
}
}
void move(char a, char b) //定义打印函数
{
printf("%c->%c\n",a,b);
}
完整代码:
#include<stdio.h>
#include<stdlib.h>
int main()
{
void hanoi(int n, char A, char B, char C);
char A='A', B='B', C='C';
int n;
scanf("%d",&n);
printf("%d层汉诺塔移动步骤为:\n",n);
hanoi(n, A, B, C);
return 0;
}
void hanoi(int n, char A, char B, char C) //实现n层塔从A借助B移动到C。
{
void move(char a, char b);
if(n==1)
move(A, C);
else
{
hanoi(n-1, A, C, B); //前n-1层从A借助C移动到B
move(A, C); //第n层从A移到C
hanoi(n-1, B, A, C); //移动到B的n-1层借助A移动到C
}
}
void move(char a, char b) //定义打印函数
{
printf("%c->%c\n",a,b);
}
运行结果(n=3为例,因为n=64步骤实在是太多了):

3.3 爬楼梯递归问题
楼梯有n阶台阶,上楼可以一步上1阶,也可以一步上2阶,还可以一步上3阶,编一程序计算共有多少种不同的走法?
分析:重点在最后一步,最后一步有三种走法,即:上1阶;上2阶,上3阶。假设最后一步上1阶,则继续考虑前n-1步走法(应用递归),最终所有的走法有lad(n-1)+lad(n-2)+lad(n-3)种。
函数代码:
int lad(int n) //定义函数
{
if(n==1)
return 1;
else if(n==2)
return 2;
else if(n==3)
return 4;
else
return lad(n-1)+lad(n-2)+lad(n-3); //
}
完整代码:
#include <stdio.h>
#include <stdlib.h>
int main()
{
int lad(int n);
int n;
scanf("%d",&n);
printf("%d",lad(n));
return 0;
}
int lad(int n)
{
if(n==1)
return 1;
else if(n==2)
return 2;
else if(n==3)
return 4;
else
return lad(n-1)+lad(n-2)+lad(n-3);
}
运行结果:
4.总结
递归的关键就是从尾巴入手,找出最后一步和前n-1步的关系,同时列出初值条件。
边栏推荐
猜你喜欢
非科班毕业生,五面阿里:四轮技术面+HR一面已拿offer
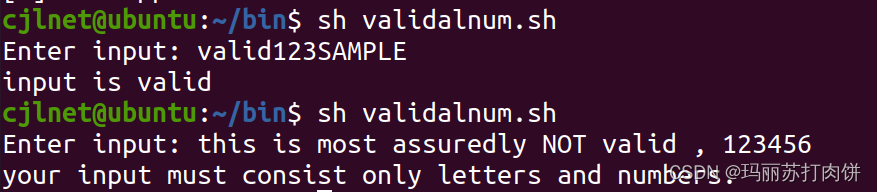
shell脚本实战(第2版)/人民邮电出版社 脚本2 验证输入:仅限字母和数字
备战金三银四:如何成功拿到阿里offer(经历+面试题+如何准备)
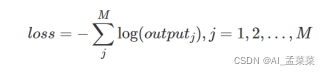
史上最小白之《Word2vec》详解
想了解API接口,这一篇就够了
Getting Started with MNIST Machine Learning
Netscope: Online visualization tool for neural network structures
jmeter BeanShell 后置处理器
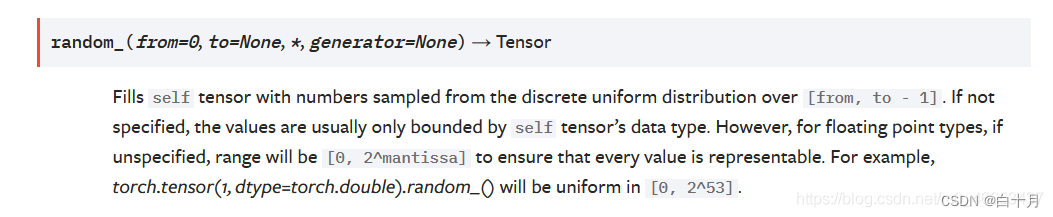
pytorch widedeep文档
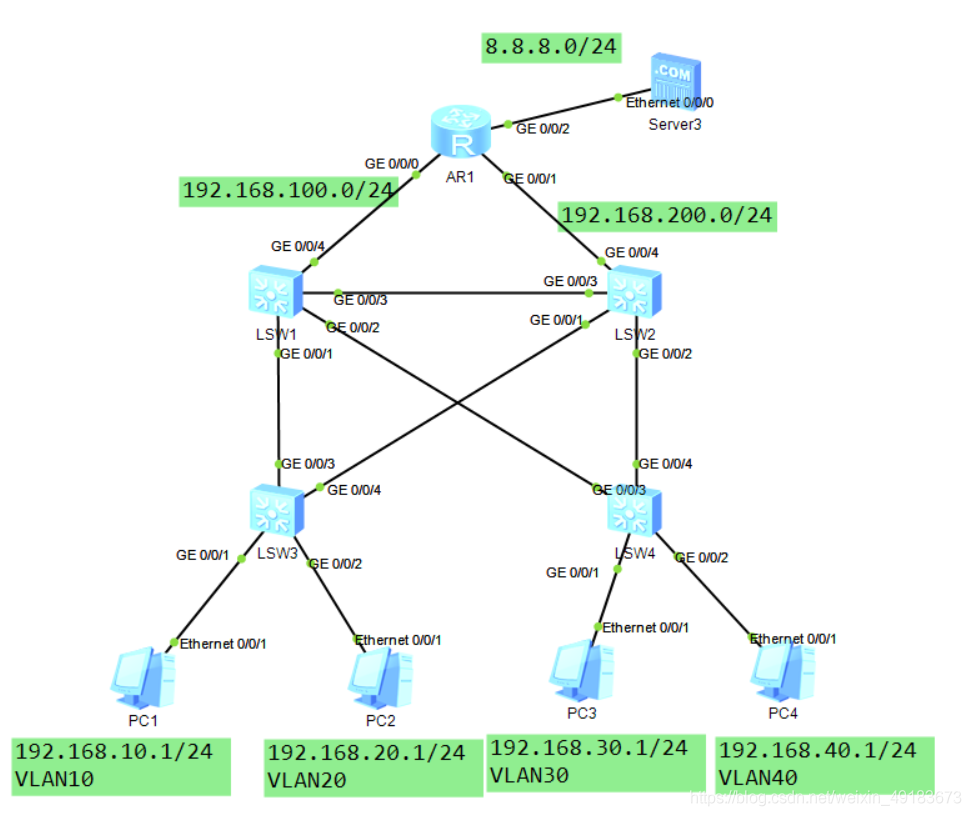
华为VRRP+MSTP联动接口检测实验案例
随机推荐
支付宝小程序的接入
从位图到布隆过滤器
OneNote 教程,如何在 OneNote 中搜索和查找笔记?
Netscope:神经网络结构在线可视化工具
Solve 1. tensorflow runs using CPU but not GPU 2. GPU version number in tensorflow environment 3. Correspondence between tensorflow and cuda and cudnn versions 4. Check cuda and cudnn versions
ThreadLocal及其内存泄露分析
研发需求的验收标准应该怎么写? | 敏捷实践
Tensorflow realize parameter adjustment of linear equations
机器学习-逻辑回归(logistics regression)
torch.cat()函数的官方解释,详解以及例子
OpenSSF的开源软件风险评估工具:Scorecards
TensorFlow: NameError: name 'input_data' is not defined
1004 成绩排名 (20 分)
Oracle数据库常用函数总结
Transformer+Embedding+Self-Attention原理详解
numpy的ndarray取数操作
类与对象 (下)
15.8 the semaphore Unix environment programming chapter 15
pytorch widedeep文档
unix系统编程 第十五章 15.2管道