当前位置:网站首页>深度學習筆記(二)——激活函數原理與實現
深度學習筆記(二)——激活函數原理與實現
2022-04-23 03:30:00 【二兩酥肉】
深度學習筆記(二)——激活函數原理與實現
閑聊
昨天詳細推了下交叉熵,感覺還可以,今天繼續加油。

ReLU
原理
定義:ReLU是修正線性單元(rectified linear unit),在0和x之間取最大值。
出現原因:由於sigmoid和tanh容易出現梯度消失,為了訓練深層神經網絡,需要一個激活函數神經網絡,它看起來和行為都像一個線性函數,但實際上是一個非線性函數,允許學習數據中的複雜關系 。該函數還必須提供更靈敏的激活和輸入,避免飽和。而ReLU是非飽和激活函數,不容易發生梯度消失。
def ReLU(input):
if input>0:
return input
else:
return 0
ReLU 的函數錶達式:
當 x <= 0 時,ReLU = 0
當 x > 0 時,ReLU = x
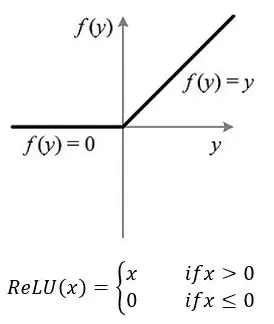
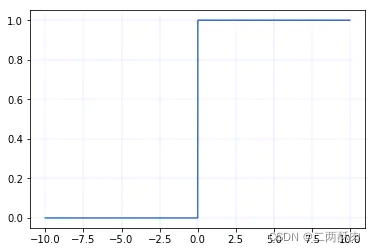
ReLU 的導數錶達式:
當 x<= 0 時,導數為 0
當 x > 0 時,導數為 1
優點
計算簡單
因為ReLU只需要一個max()函數便可以完成運算,而tanh和sigmoid需要指數運算,所以ReLU計算成本很低。
代錶性稀疏
ReLU在負輸入時可以輸出真零值,允許神經網絡中的隱藏層包含一個或多個真零值,這就是所謂的稀疏錶示。在錶示學習,因為它可以加速學習和簡化模型。有效緩解過擬合的問題,因為 ReLU 有可能使部分神經節點的輸出變為 0,從而導致神經節點死亡,降低了神經網絡的複雜度。
線性行為
在輸入大於零時,ReLU看起來像一個線性函數,當網絡行為是近線性時,更容易優化,不會發生梯度消失或梯度爆炸,當 x 大於 0 時,ReLU 的梯度恒為 1,不會隨著網路深度的加深而使得梯度在累乘的時候變得越來越小或者越來越大,從而不會發生梯度消失或梯度爆炸,也因此可以更適合訓練深度網絡。現在深度學習中,默認的激活函數是ReLU。
缺點
不適合RNN類網絡
對 MLPs,CNNs 使用 ReLU,但不是 RNNs。ReLU 可以用於大多數類型的神經網絡,它通常作為多層感知機神經網絡和卷積神經網絡的激活函數 。傳統上,LSTMs 使用 tanh 激活函數來激活cell狀態,使用 Sigmoid激活函數作為node輸出。而ReLU通常不適合RNN類型網絡的使用。
代碼
import torch
import torch.nn as nn
relu = nn.ReLU(inplace=True)
Sigmoid
原理
Sigmoid 是常用的非線性的激活函數,可以將全體實數映射到(0, 1)區間上,其采用非線性方法將數據進行歸一化處理;sigmoid函數通常用在回歸預測和二分類(即按照是否大於0.5進行分類)模型的輸出層中。
函數公式:
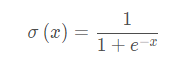
def Sigmoid(x):
return 1. / (1 + np.exp(-x))
曲線圖:
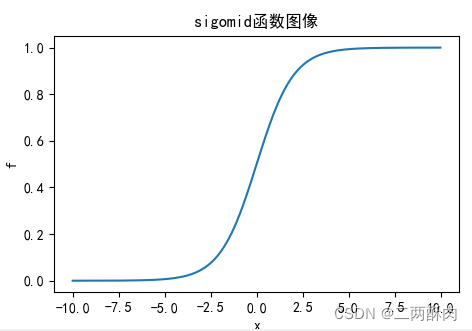
導數:

導數圖像:
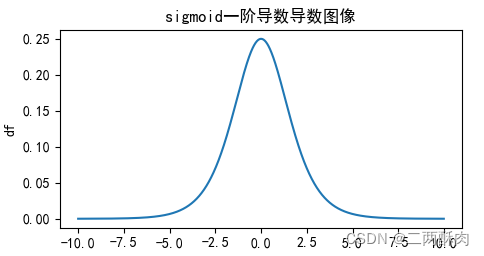
優點
求導容易
梯度平滑,求導容易
優化穩定
Sigmoid函數的輸出映射在(0,1)之間,單調連續,輸出範圍有限,優化穩定,可以用作輸出層
缺點
計算量大
在正向傳播和反向傳播中都包含幂運算和除法,所以存在著較大計算資源。
梯度消失
梯度消失:輸入值較大或較小(圖像兩側)時,sigmoid導數則接近於零,因此在反向傳播時,這個局部梯度會與整個代價函數關於該單元輸出的梯度相乘,結果也會接近為 0 ,無法實現更新參數的目的;
關於這點可以從其導數圖像中看出,如果我們初始化神經網絡的權值為 [0,1] [0,1][0,1] 之間的隨機值,由反向傳播算法的數學推導可知,梯度從後向前傳播時,每傳遞一層梯度值都會减小為原來的0.25倍,如果神經網絡隱層特別多,那麼梯度在穿過多層後將變得非常小接近於0,即出現梯度消失現象;
代碼
import torch
import torch.nn as nn
sigmoid=nn.Sigmoid()
Softmax
原理
Sigmoid函數只能處理兩個類別,這不適用於多分類的問題,所以Softmax可以有效解决這個問題。Softmax函數很多情况都運用在神經網路中的最後一層網絡中,使得每一個類別的概率值在(0, 1)之間。Softmax =多類別分類問題=只有一個正確答案=互斥輸出(例如手寫數字,鳶尾花)。構建分類器,解决只有唯一正確答案的問題時,用Softmax函數處理各個原始輸出值。Softmax函數的分母綜合了原始輸出值的所有因素,這意味著,Softmax函數得到的不同概率之間相互關聯。即得到的所有概率和為1,示例看代碼部分

def softmax(x):
return np.exp(x) / sum(np.exp(x))

優點
適用範圍較廣
相較於sigmoid,softmax可以處理多分類問題,因此可以適用於更多領域。
拉開值之間差距
由於Softmax函數先拉大了輸入向量元素之間的差异(通過指數函數),然後才歸一化為一個概率分布,在應用到分類問題時,它使得各個類別的概率差异比較顯著,最大值產生的概率更接近1,這樣輸出分布的形式更接近真實分布。由於其拉開了差距,這樣便於提高loss,能够獲得更多的學習效果。
代碼
舉例:
假如一個雞鴨鹅的三分類數據集,假如一個batch有三個輸入,通過之前的網絡,得到結果是([10,8,6],[7,9,5],[5,4,10])。
實際的標簽值為[0,1,2],即是雞鴨鹅。
錶示含義是:網絡推測雞的概率為[86.68%],鴨[11.73%],鹅[1.59%],後面兩行同理。
import torch
import torch.nn as nn
import math
import time
# 假設結果
input_1=torch.Tensor([0,1,2])
# 預測結果
input_2 = torch.Tensor([
[10,8,6],
[7,9,5],
[5,4,10]
])
#規定不同方向的softmax
softmax = nn.Softmax(dim=1)
#對不同維度的張量試驗
output = softmax(input_2)
print(output)
#------------#
#tensor([[0.8668, 0.1173, 0.0159],
# [0.1173, 0.8668, 0.0159],
# [0.0067, 0.0025, 0.9909]])
#------------#
Tanh
原理
公式:
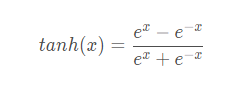
def tanh(x):
return np.sinh(x)/np.cosh(x)
函數圖像
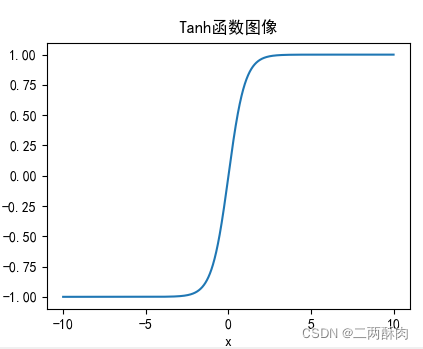
一階求導後函數形式:

求導函數圖像:

優點
收斂快
比Sigmoid函數收斂速度更快
梯度消失問題較輕
tanh(x) 的梯度消失問題比 sigmoid 要輕。因為可以看出,sigmoid在接近0時每層會縮小0.25倍,而tanh可以接近1,所以在深層網絡中,梯度消失問題得到了减輕。
輸出以0為中心
相比Sigmoid函數,輸出是以 0 為中心 zero-centered
缺點
計算消耗量大
可以看出其進行了幾次指數運算,消耗了比較大的計算成本。
梯度消失仍然存在
從導數圖像可以看出,其導數圖像和sigmoid有很大的相似性,還是沒有改變Sigmoid函數的最大問題——由於飽和性產生的梯度消失。
代碼
import torch
import torch.nn as nn
relu = nn.tanh()
LeakyReLU
原理
Leaky ReLU 是為解决“ ReLU 死亡”問題的嘗試。主要是為了避免死亡ReLU:x小於0時候,導數是一個小的數值,而不是0。

通常a為0.01。
def ReLU(input):
if input>0:
return input
else:
return 0.01*input
優點
計算成本低
計算快速:不包含指數運算。
能得到負值輸出
相較於ReLU可以得到負值輸出
擁有ReLU其他優點
缺點
a是超參數,需要人工設定
兩部分都是線性
代碼
import torch
import torch.nn as nn
LR=nn.LeakyReLU(inplace=True)
ReLU6
原理
主要是為了在移動端float16的低精度的時候,也能有很好的數值分辨率,如果對ReLu的輸出值不加限制,那麼輸出範圍就是0到正無窮,而低精度的float16無法精確描述其數值,帶來精度損失。

特點
基本和ReLU相同,只是輸出值上限有了限制。
def ReLU(input):
if input>0:
return min(6,input)
else:
return 0
代碼
"""pytorch 神經網絡"""
import torch.nn as nn
Re=nn.ReLU6(inplace=True)
ELU
原理
LU 的提出也解决了ReLU 的問題。與ReLU相比,ELU有負值,這會使激活的平均值接近零。均值激活接近於零可以使學習更快,因為它們使梯度更接近自然梯度。

函數圖像:

優點
解决了Dead ReLU
沒有Dead ReLU問題,輸出的平均值接近0,以0為中心。
加速學習
ELU 通過减少偏置偏移的影響,使正常梯度更接近於單比特自然梯度,從而使均值向零加速學習。
减少變异和信息
ELU函數在較小的輸入下會飽和至負值,從而减少前向傳播的變异和信息。
缺點
計算量變大
ELU函數的計算强度更高。與Leaky ReLU類似,盡管理論上比ReLU要好,但目前在實踐中沒有充分的證據錶明ELU總是比ReLU好。
代碼
import torch
import torch.nn as nn
LR=nn.ELU()
# ELU函數在numpy上的實現
import numpy as np
import matplotlib.pyplot as plt
def elu(x, a):
y = x.copy()
for i in range(y.shape[0]):
if y[i] < 0:
y[i] = a * (np.exp(y[i]) - 1)
return y
if __name__ == '__main__':
x = np.linspace(-50, 50)
a = 0.5
y = elu(x, a)
print(y)
plt.plot(x, y)
plt.title('elu')
plt.axhline(ls='--',color = 'r')
plt.axvline(ls='--',color = 'r')
# plt.xticks([-60,60]),plt.yticks([-10,50])
plt.show()
SELU
原理
SELU 源於論文 Self-Normalizing Neural Networks,作者為 Sepp Hochreiter,ELU 同樣來自於他們組。
SELU 其實就是 ELU 乘 lambda,關鍵在於這個 lambda 是大於 1 的,論文中給出了 lambda 和 alpha 的值:
- lambda = 1.0507
- alpha = 1.67326
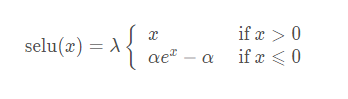
函數圖像:
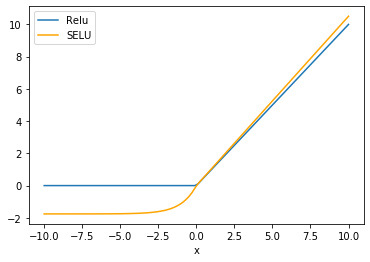
優點
自歸一化
SELU 激活能够對神經網絡進行自歸一化(self-normalizing);
不出現梯度消失或爆炸
不可能出現梯度消失或爆炸問題,論文附錄的定理 2 和 3 提供了證明。
缺點
應用較少
應用較少,需要更多驗證;
需要初始化
lecun_normal 和 Alpha Dropout:需要 lecun_normal 進行權重初始化;如果 dropout,則必須用 Alpha Dropout 的特殊版本。
代碼
import torch
import torch.nn as nn
SELU=nn.SELU()
Parametric ReLU (PRELU)
原理
形式上與 Leak_ReLU 在形式上類似,不同之處在於:PReLU 的參數 alpha 是可學習的,需要根據梯度更新。
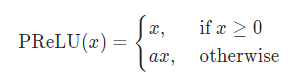
- alpha=0:退化為 ReLU
- alpha 固定不更新,退化為 Leak_ReLU

優點
與 ReLU 相同。
缺點
在不同問題中,錶現不一。
代碼
import torch
import torch.nn as nn
PReLU= nn.PReLU()
Gaussian Error Linear Unit(GELU)
原理
高斯誤差線性單元激活函數在最近的 Transformer 模型(穀歌的 BERT 和 OpenAI 的 GPT-2)中得到了應用。GELU 的論文來自 2016 年,但直到最近才引起關注。


優點
效果好
似乎是 NLP 領域的當前最佳;尤其在 Transformer 模型中錶現最好;
避免梯度消失
能避免梯度消失問題。
缺點
這個2016 年提出的新穎激活函數還缺少實際應用的檢驗。
代碼
import torch
import torch.nn as nn
gelu_f== nn.GELU()
import torch
import torch.nn as nn
import torch.nn.functional as F
import numpy as np
from matplotlib import pyplot as plt
class GELU(nn.Module):
def __init__(self):
super(GELU, self).__init__()
def forward(self, x):
return 0.5*x*(1+F.tanh(np.sqrt(2/np.pi)*(x+0.044715*torch.pow(x,3))))
def gelu(x):
return 0.5*x*(1+np.tanh(np.sqrt(2/np.pi)*(x+0.044715*np.power(x,3))))
x = np.linspace(-4,4,10000)
y = gelu(x)
plt.plot(x, y)
plt.show()
Swish
原理
Swish激活函數誕生於Google Brain 2017的論文 Searching for Activation functions中,其定義為:

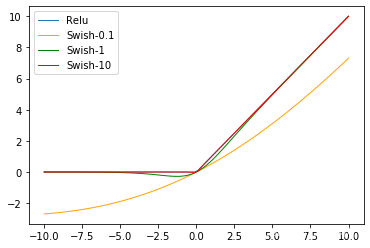
β是個常數或可訓練的參數.
Swish 在深層模型上的效果優於 ReLU。例如,僅僅使用 Swish 單元替換 ReLU 就能把 Mobile NASNetA 在 ImageNet 上的 top-1 分類准確率提高 0.9%,Inception-ResNet-v 的分類准確率提高 0.6%。
特點
Swish 具備無上界有下界、平滑、非單調的特性。
代碼
import torch
import torch.nn as nn
class Swish(nn.Module):
def __init__(self):
super(Swish, self).__init__()
def forward(self, x):
x = x * F.sigmoid(x)
return x
Swi=Swish()
函數求導作圖代碼
對
import sympy as sy #用於求導積分等數學計算
import matplotlib.pyplot as plt #繪圖
import numpy as np
x = sy.symbols('x') #定義符號變量x
#sigmoid函數
f = 1. / (1 + sy.exp(-x))
df = sy.diff(f,x) #求一階導數
#ddf = sy.diff(df,x)
ddf = sy.diff(f,x,2) #求二階導數,參數2為求導階數
#建立空列錶用來保存數據
x_value = [] #保存自變量x的取值
f_value = [] #保存函數值f的取值
df_value = [] #保存一階導數df的取值
for i in np.arange(-10,10,0.01):
x_value.append(i)#對x進行取值
f_value.append(f.subs('x',i))#將i值代入錶達式
df_value.append(df.subs('x',i))#將i值代入求導錶達式
#正常顯示中文需要一下兩行代碼
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False
plt.title('sigomid函數圖像')
plt.xlabel('x')
plt.ylabel('f')
plt.plot(x_value,f_value)
plt.show()
plt.title('sigmoid一階導數導數圖像')
plt.xlabel('x')
plt.ylabel('df')
plt.plot(x_value,df_value)
plt.show()
版权声明
本文为[二兩酥肉]所创,转载请带上原文链接,感谢
https://yzsam.com/2022/04/202204230326525434.html
边栏推荐
- Using jsonserialize to realize data type conversion gracefully
- Explication détaillée des fonctions send () et recv () du programme Socket
- L3-011 direct attack Huanglong (30 points)
- C set
- Batch download of files ---- compressed and then downloaded
- 场景题:A系统如何使用B系统的页面
- Can you answer the questions that cannot be answered with a monthly salary of 10k-20k?
- Section 2 map and structure in Chapter 6
- Chapter 8 exception handling, string handling and file operation
- Un aperçu des flux d'E / s et des opérations de fichiers de classe de fichiers
猜你喜欢

Optimization of especially slow startup in idea debugging mode

Unity basics 2
you need to be root to perform this command

Design and implementation of redis (2): how to handle expired keys
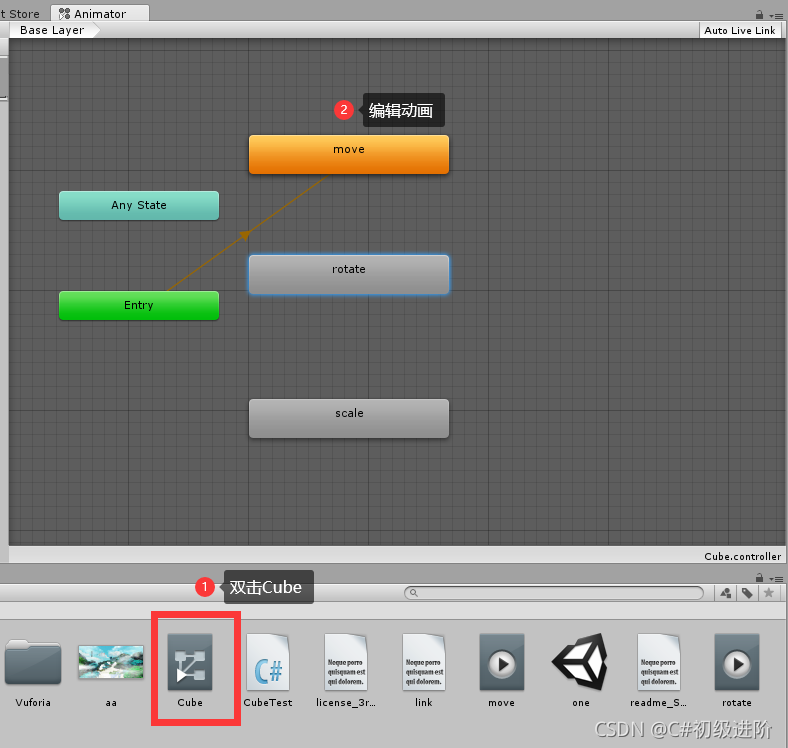
Unity Basics
PYMOL-note

Codeforces Round #784 (Div. 4)题解 (第一次AK cf (XD

深度学习笔记(二)——激活函数原理与实现
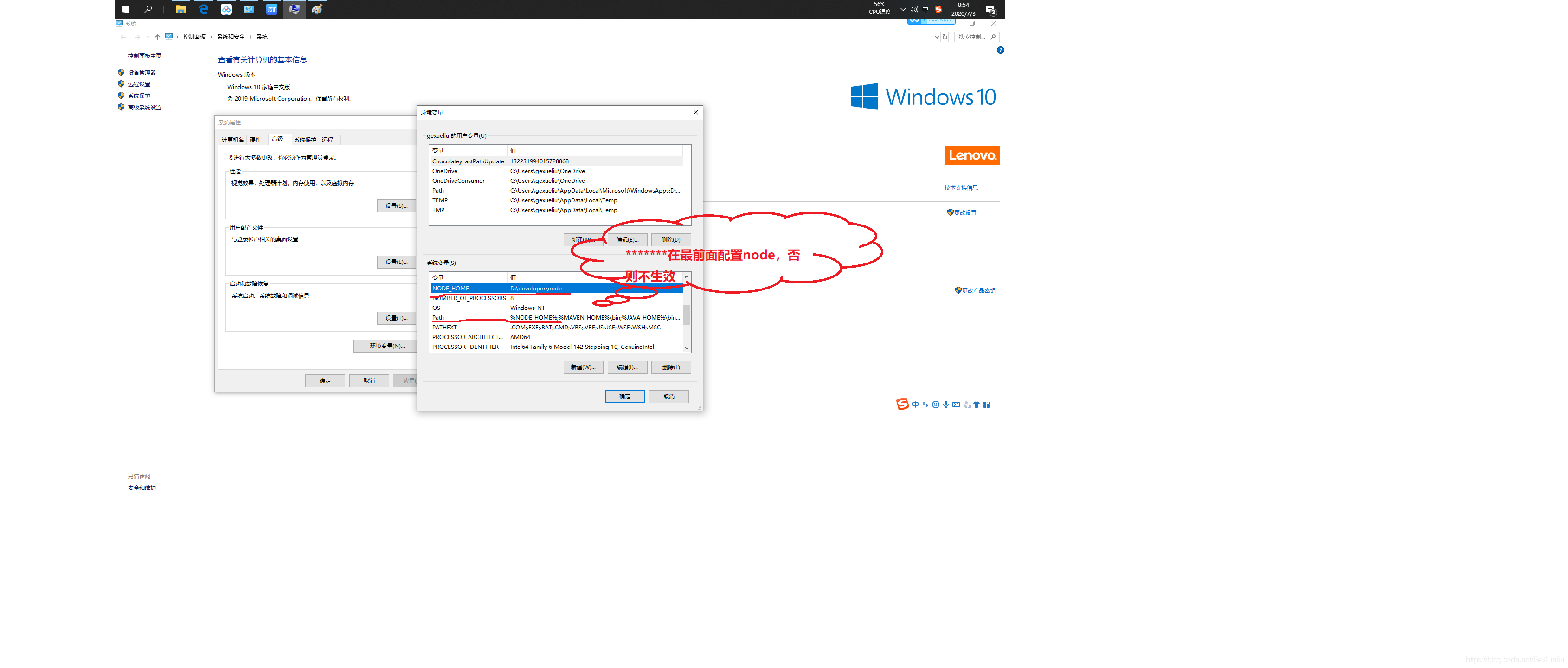
Node configuration environment CMD does not take effect

Download and configuration of idea
随机推荐
2022 group programming ladder simulation match 1-8 are prime numbers (20 points)
The content of the website is prohibited from copying, pasting and saving as JS code
WinForm allows the form form to switch between the front and active states
Explication détaillée des fonctions send () et recv () du programme Socket
. net webapi access authorization mechanism and process design (header token + redis)
Download and configuration of idea
2022 团体程序设计天梯赛 模拟赛 1-8 均是素数 (20 分)
Using jsonserialize to realize data type conversion gracefully
通过 zxing 生成二维码
Supersocket is Used in net5 - command
MySQL索引详解【B+Tree索引、哈希索引、全文索引、覆盖索引】
ThreadLocal test multithreaded variable instance
POI create and export Excel based on data
Flink customizes the application of sink side sinkfunction
Unity knowledge points (ugui)
JS - accuracy issues
File upload vulnerability summary and upload labs shooting range documentary
Code forces round # 784 (DIV. 4) solution (First AK CF (XD)
Visual programming -- how to customize the mouse cursor
poi根据数据创建导出excel