当前位置:网站首页>1007 go running (hdu6808) in the fourth game of 2020 Hangzhou Electric Multi school competition
1007 go running (hdu6808) in the fourth game of 2020 Hangzhou Electric Multi school competition
2022-04-23 06:29:00 【cornivores】
1007 Go Running(hdu6808)
The question : There is an infinite runway , Some people are 1m/s Run at a constant speed , There is a detector in t i t_i ti A classmate is detected in x i x_i xi The location of , Ask at least how many people are running .
solution : First, you can establish a rectangular coordinate system , The abscissa represents time , The ordinate represents the position , about 1m/s Moving at a constant speed , Then the slope of a person's trajectory in such a coordinate system must be 1 or -1, Then the meaning of the question can be transformed into the slope of these points as 1 and -1 Draw a straight line , Then look at the least straight line passing through all points .

If you turn this picture clockwise 45 degree , It can be thought that this is a classical problem of bipartite graph matching , Minimum point coverage = The biggest match , Here I use the method of network flow to realize , Establish super source and super sink . The specific edge building method is that the source point is connected to all the involved exercise weight values are 1( Pay attention to the repetition without superposition ), The weight of all involved column connecting sinks is 1( Note that repetition does not overlap ), Then, for each point row and column, a weight of 1 The edge of , Just run one side to the maximum flow .
Code :
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5+10;
const int M = 2e5+10;
const int INF = 0x3f3f3f3f;
struct xx {
int x, y, a, b, lx, ly;
}p[N];
bool cmp1(const xx &p1, const xx &p2) {
return p1.a < p2.a;
}
bool cmp2(const xx &p1, const xx &p2) {
return p1.b > p2.b;
}
struct node {
int to, dis, next;
}Ed[M*2];
int head[M], cur[M], d[M], cnt = 1;
int tot, lst, s, t;
void Add(int from, int to, int dis) {
Ed[++cnt] = node {
to, dis, head[from]};
head[from] = cnt;
Ed[++cnt] = node {
from, 0, head[to]};
head[to] = cnt;
}
bool bfs() {
memset(d, -1, sizeof(d));
queue<int>q;q.push(s);
int u, _new;
d[s] = 0;
while(!q.empty()) {
u = q.front(); q.pop();
for(int c_e = head[u]; c_e != -1; c_e = Ed[c_e].next) {
// Zengguang road
_new = Ed[c_e].to;
if(d[_new] == -1 && Ed[c_e].dis > 0) {
d[_new] = d[u] + 1;
q.push(_new);
}
}
}
return (d[t] != -1);
}
int dfs(int u, int flow) {
//cout << u << " " << flow << endl;
if(u == t) return flow;
int _flow = 0, __flow;
for(int &c_e = cur[u]; c_e != -1; c_e = Ed[c_e].next) {
// Current arc optimization
int v = Ed[c_e].to;
if(d[v] == d[u] + 1 && Ed[c_e].dis > 0) {
__flow = dfs(v, min(flow, Ed[c_e].dis));
flow -= __flow;
Ed[c_e].dis -= __flow;
_flow += __flow;
Ed[c_e^1].dis += __flow;
if(!flow) break;
}
}
if(!_flow) d[u] = -1;
return _flow;
}
void dinic() {
int max_flow = 0;
while(bfs()) {
for(int i = 0; i <= t; ++i) cur[i] = head[i];
max_flow += dfs(s, INF);
}
printf("%d\n", max_flow);
}
int vis[M];
int main() {
int T; scanf("%d", &T);
int n;
while(T--) {
scanf("%d", &n);
for(int i = 1; i <= n; ++i) {
scanf("%d%d", &p[i].x, &p[i].y);
p[i].a = p[i].x + p[i].y;
p[i].b = p[i].y - p[i].x;
}
sort(p+1, p+n+1, cmp1);
tot = 1, lst = p[1].a;
p[1].ly = tot;
for(int i = 2; i <= n; ++i) {
if(p[i].a == lst) p[i].ly = tot;
else p[i].ly = ++tot;
lst = p[i].a;
}
sort(p+1, p+n+1, cmp2);
lst = p[1].b;
p[1].lx = ++tot;
for(int i = 2; i <= n; ++i) {
if(p[i].b == lst) p[i].lx = tot;
else p[i].lx = ++tot;
lst = p[i].b;
}
// Jianbian
cnt = 1;
s = 0; t = tot+1;
for(int i = 0; i <= t; ++i) head[i] = -1, vis[i] = 0;
for(int i = 1; i <= n; ++i) {
if(!vis[p[i].lx]) Add(s, p[i].lx, 1), vis[p[i].lx] = 1;
Add(p[i].lx, p[i].ly, 1);
if(!vis[p[i].ly]) Add(p[i].ly, t, 1), vis[p[i].ly] = 1;
}
dinic();
}
return 0;
}
版权声明
本文为[cornivores]所创,转载请带上原文链接,感谢
https://yzsam.com/2022/04/202204210615591783.html
边栏推荐
猜你喜欢
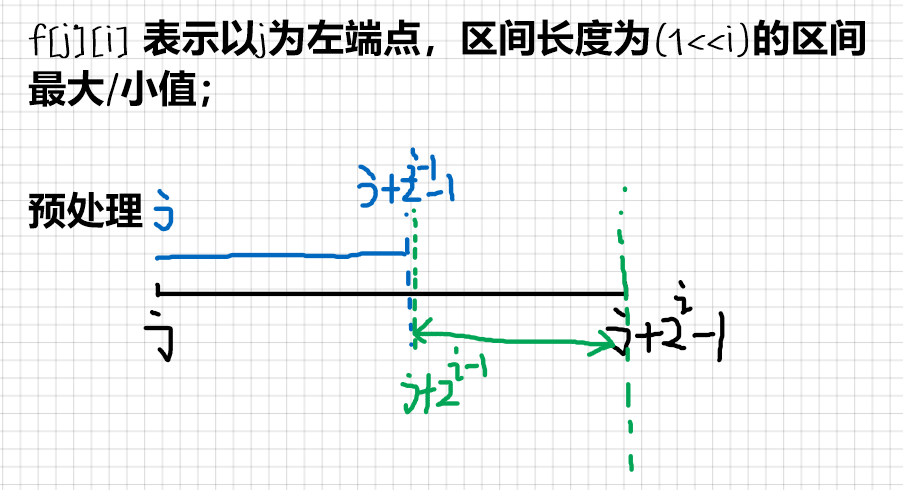
St table template

The bottom implementation principle of thread - static agent mode
Motor and drive (Qi Jinqing Edition)

Delete and truncate

SQL -- data filtering and grouping

Substring Inversion (Easy Version)

P1586 solution to tetragonal theorem
电机与拖动(戚金清版)学习整理

lambda expressions
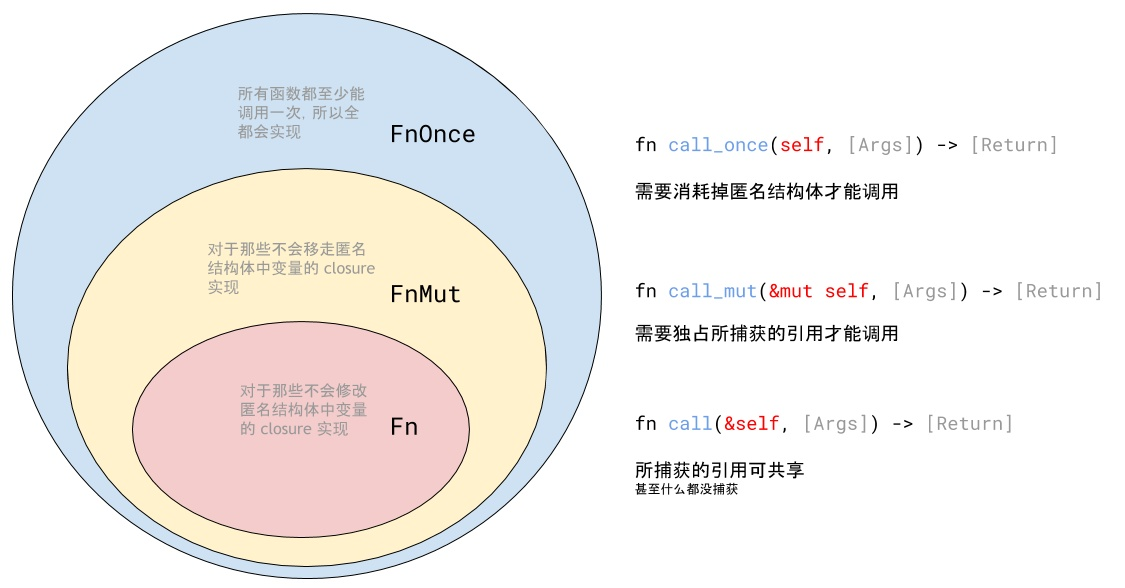
Rust的闭包类型(Fn, FnMut, FnOne的区别)
随机推荐
Detection technology and principle
檢測技術與原理
PHP processing JSON_ Decode() parses JSON stringify
The bottom implementation principle of thread - static agent mode
6.Reversal
Common sense of thread pool
Rust:如何实现一个线程池?
serde - rust的序列化方案
[leetcode 202] happy number
Integration and induction of knowledge points of automatic control principle (Han min version)
20 excellent plug-ins recommended by idea
Gesture recognition research
@Problems caused by internal dead loop of postconstruct method
Guaba and Computational Geometry
解决ArcGIS分区统计显示太多唯一值执行失败
检测技术与原理
11.a==b?
Framework analysis 2 Source code - login authentication
H. Are You Safe? Convex hull naked problem
Plane semi intersecting plate