A-Ancestor

题目大意：
给出两棵编号1-n的树A B，A B树上每个节点均有一个权值，给出k个关键点的编号𝑥_1…𝑥_𝑛，问有多少种方案使得去掉恰好一个关键点使得剩余关键点在树A上LCA的权值大于树B上LCA的权值。

思路：
预处理出关键点序列的在树A B上的前缀LCA和后缀LCA，枚举去掉的关键节点并使用前后缀LCA算出剩余节点的LCA比较权值即可。

树刨求LCA代码：

#include <bits/stdc++.h>
#define mem(a, v) memset(a, v, sizeof(a))
const int N = 2e5 + 5;
using namespace std;

struct lcatree
{
    
    int val[N];
    int dep[N], fa[N], sz[N], mson[N], top[N];

    vector<int> son[N]; //记录每个结点的子树

    void dfs1(int u) //求dep,fa,sz,mson
    {
    
        sz[u] = 1;
        mson[u] = 0;
        for (auto s : son[u])
        {
    
            dep[s] = dep[u] + 1;
            fa[s] = u;
            dfs1(s);
            sz[u] += sz[s];
            if (sz[s] > sz[mson[u]]) mson[u] = s;
        }
    }
    void dfs2(int u) //求top
    {
    
        if (u == mson[fa[u]]) // u是最大的儿子，一定在重链上，top值与父结点相同
            top[u] = top[fa[u]];
        else
            top[u] = u;
        for (auto s : son[u])
            dfs2(s);
    }
    void init(int n)
    {
    
        int f;
        for (int i = 1; i <= n; i++)
            cin >> val[i];
        for (int i = 2; i <= n; i++)
        {
    
            cin >> f;
            son[f].push_back(i);
        }
        sz[0] = 0;
        dfs1(1);
        dfs2(1);
    }
    int get_lca(int u, int v)
    {
    
        while (top[u] != top[v])
        {
    
            if (dep[top[u]] > dep[top[v]])
                u = fa[top[u]];
            else
                v = fa[top[v]];
        }
        return dep[u] < dep[v] ? u : v;
    }
} treea, treeb;

int key[N], prea[N], preb[N], lsta[N], lstb[N];

signed main()
{
    
    ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
    int n, k, ans = 0;
    cin >> n >> k;
    for (int i = 1; i <= k; i++)
        cin >> key[i];
    treea.init(n);
    treeb.init(n);
    prea[1] = key[1];
    preb[1] = key[1];
    for (int i = 2; i <= k; i++)
    {
    
        prea[i] = treea.get_lca(prea[i - 1], key[i]);
        preb[i] = treeb.get_lca(preb[i - 1], key[i]);
    }
    lsta[k] = key[k];
    lstb[k] = key[k];
    for (int i = k - 1; i >= 1; i--)
    {
    
        lsta[i] = treea.get_lca(lsta[i + 1], key[i]);
        lstb[i] = treeb.get_lca(lstb[i + 1], key[i]);
    }
    for (int i = 1; i <= k; i++)
    {
    
        if (i == 1)
        {
    
            if (treea.val[lsta[2]] > treeb.val[lstb[2]])
                ans++;
        }
        else if (i == k)
        {
    
            if (treea.val[prea[k - 1]] > treeb.val[preb[k - 1]])
                ans++;
        }
        else
        {
    
            int lcaa = treea.get_lca(prea[i - 1], lsta[i + 1]);
            int lcab = treeb.get_lca(preb[i - 1], lstb[i + 1]);
            if (treea.val[lcaa] > treeb.val[lcab])
                ans++;
        }
    }
    cout << ans;
    return 0;
}

区间RMQ求LCA代码：

#include <bits/stdc++.h>
#define mem(a, v) memset(a, v, sizeof(a))
const int N = 2e5 + 5;
using namespace std;

struct lcatree
{
    
    int pos[N];        //记录结点在欧拉序列中第一次出现的位置
    int seq[N * 2];    //记录欧拉序列
    int dep[N * 2];    //记录欧拉序列中对应下标的深度
    int st[N * 2][20]; // st表，记录深度最小的下标
    int val[N];
    int tot = 0;
    bool vis[N];

    vector<int> son[N]; //记录每个结点的子树

    void dfs(int u, int d) // 构建欧拉序列，u表示当前结点，d表示深度
    {
    
        vis[u] = 1;
        pos[u] = ++tot;
        seq[tot] = u;
        dep[tot] = d;
        for (auto s : son[u])
        {
    
            if (vis[s]) continue;
            dfs(s, d + 1);
            seq[++tot] = u; //每次回溯要将当前点再次加入欧拉序列
            dep[tot] = d;
        }
    }
    void st_create() //创建st表
    {
    
        for (int i = 1; i <= tot; i++)
            st[i][0] = i;
        int k = log2(tot), f1, f2;
        for (int j = 1; j <= k; j++)
        {
    
            for (int i = 1; i <= tot - (1 << j) + 1; i++)
            {
    
                f1 = st[i][j - 1], f2 = st[i + (1 << (j - 1))][j - 1];
                st[i][j] = dep[f1] < dep[f2] ? f1 : f2;
            }
        }
    }
    int get_lca(int u, int v)
    {
    
        int l = pos[u], r = pos[v];
        if (l > r) swap(l, r);
        int k = log2(r - l + 1);
        int f1 = st[l][k], f2 = st[r - (1 << k) + 1][k];
        return dep[f1] < dep[f2] ? seq[f1] : seq[f2]; //返回时要将下标转化成seq数组中的值
    }

    void init(int n)
    {
    
        mem(vis, 0);
        int fa;
        for (int i = 1; i <= n; i++)
            cin >> val[i];
        for (int i = 2; i <= n; i++)
        {
    
            cin >> fa;
            son[fa].push_back(i);
        }
        dfs(1, 0);
        st_create();
    }
} treea, treeb;

int key[N], prea[N], preb[N], lsta[N], lstb[N];

signed main()
{
    
    ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
    int n, k, ans = 0;
    cin >> n >> k;
    for (int i = 1; i <= k; i++)
        cin >> key[i];
    treea.init(n);
    treeb.init(n);
    prea[1] = key[1];
    preb[1] = key[1];
    for (int i = 2; i <= k; i++)
    {
    
        prea[i] = treea.get_lca(prea[i - 1], key[i]);
        preb[i] = treeb.get_lca(preb[i - 1], key[i]);
    }
    lsta[k] = key[k];
    lstb[k] = key[k];
    for (int i = k - 1; i >= 1; i--)
    {
    
        lsta[i] = treea.get_lca(lsta[i + 1], key[i]);
        lstb[i] = treeb.get_lca(lstb[i + 1], key[i]);
    }
    for (int i = 1; i <= k; i++)
    {
    
        if (i == 1)
        {
    
            if (treea.val[lsta[2]] > treeb.val[lstb[2]])
                ans++;
        }
        else if (i == k)
        {
    
            if (treea.val[prea[k - 1]] > treeb.val[preb[k - 1]])
                ans++;
        }
        else
        {
    
            int lcaa = treea.get_lca(prea[i - 1], lsta[i + 1]);
            int lcab = treeb.get_lca(preb[i - 1], lstb[i + 1]);
            if (treea.val[lcaa] > treeb.val[lcab])
                ans++;
        }
    }
    cout << ans;
    return 0;
}

D-Directed

题目大意：
在一棵树上选择一个起点s，终点为1，每次随机地走到相邻的点，随机地选择k条边令其变成指向终点的有向边，求出从s走到1的期望步数。

思路：
用F[x]表示从x走到父结点的期望步数，那么答案就是将s到1这条路径上的F值加起来。
对于x，可能一步走到父结点，也可能先走到子树（走到每个子树的概率为1/degx，degx为x的边数），然后从子树走回来。
那么F[x]的表达式就是：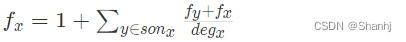

进行移项得到：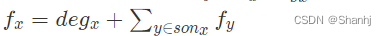

如果把这个式子中的fy再展开的话，可以发现F[x]其实就等于1+2倍的子树大小（可以画一棵简单的树来验证）。

也就是x中每个子结点对F[x]的贡献为2，对于整棵树来说，每个点对答案的贡献等于这个点到1上经过的关键点数量乘2(1不算入关键点，因为1已经是终点了)，然后加上关键点的数量就是答案了。

这是k为0的情况，如果要随机选择k条边成为有向边的话，一个点对关键路径上的点有贡献的情况是这个点到关键路径上的边不存在有向边。假设这个点到关键路径要经过i条边，这个概率等于在(n-i-1)条边中选k条成为有向边。

但是计算每个点对关键点的贡献是n²的复杂度，是无法接受的。必须一次就将这个点对答案的贡献算出来，如果把每个点对关键点的贡献都列出来，其实就相当于计算C(n-i-1,k)+C(n-i-2,k)+…+C(n-j-1,k)，可以用前缀和处理。

AC代码：

#include <bits/stdc++.h>
#define mem(a, v) memset(a, v, sizeof(a))
const int N = 1e6 + 5;
const long long mod = 998244353ll;
using namespace std;

long long sum[N], fac[N], facinv[N], invc, ans = 0;
int fa[N], dep[N], n, k, s;
bool keypath[N];
vector<int> g[N];

long long ksm(long long base, long long power, long long mod)
{
    
    long long result = 1;
    base %= mod;
    while (power)
    {
    
        if (power & 1)
            result = (result * base) % mod;
        power >>= 1;
        base = (base * base) % mod;
    }
    return result;
}
//从a个里面挑b个
long long C(int a, int b) {
     return fac[a] * facinv[b] % mod * facinv[a - b] % mod; }

void init()
{
    
    mem(keypath, 0);

    facinv[0] = fac[0] = 1;
    for (long long i = 1; i < N; i++)
        fac[i] = fac[i - 1] * i % mod;
    facinv[N - 1] = ksm(fac[N - 1], mod - 2, mod);
    for (long long i = N - 2; i >= 1; i--)
        facinv[i] = facinv[i + 1] * (i + 1) % mod;

    sum[0] = 0; //预处理C(k,n-1)~C(k,n-1-i)的前缀和
    for (int i = 1; i <= n; i++)
        sum[i] = C(n - 1 - i, k) + sum[i - 1];
    invc = ksm(C(n - 1, k), mod - 2, mod);
}

void dfs1(int u, int deep) //计算每个点的深度和父结点
{
    
    dep[u] = deep;
    for (auto v : g[u])
    {
    
        if (v == fa[u]) continue;
        fa[v] = u;
        dfs1(v, deep + 1);
    }
}

void dfs2(int u, int f) //找到u的父亲中最近的关键路径上的点
{
    
    for (auto v : g[u])
    {
    
        if (v == f) continue;
        if (keypath[u])
            fa[v] = u;
        else
            fa[v] = fa[u];
        dfs2(v, u);
    }
}

signed main()
{
    
    ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
    cin >> n >> k >> s;
    init();
    int u, v;
    for (int i = 2; i <= n; i++)
    {
    
        cin >> u >> v;
        g[u].push_back(v);
        g[v].push_back(u);
    }
    fa[1] = 0;
    dfs1(1, -1); //将结点1的深度设为-1，方便后续计算

    for (int i = s; i; i = fa[i]) //将关键路径进行染色
        keypath[i] = 1;

    dfs2(1, 0);

    for (int i = 2; i <= n; i++)
        if (fa[i]) //计算每个点对答案的贡献,在根的其他子树上的点不会对答案有贡献
            ans = (ans + (sum[dep[i]] - sum[dep[i] - dep[fa[i]] - 1] + mod) * 2 % mod * invc % mod) % mod;

    ans = (ans + dep[s] + 1) % mod; //最后加上关键路径上的点自己对答案的贡献（也就是关键路径上的点数-1）
    cout << ans;
    return 0;
}

F-Fief

题目大意：
在一个图上找两个点x和y，判断是否所有的点都能在不经过y或x的情况下到达x或y。也就是将所有的点排成某个顺序，使得这个顺序前后缀都连通。

最简化的题意就是：
能否将图缩成一条链（双连通分量缩点），且x和y位于链的两端。

前置知识：
割点、双连通分量

思路：
首先得判断图是否连通，如果图都不连通那就不存在解。
然后找出图中的双连通分量，计算每个双连通分量的度，如果每个双连通分量的度都不大于2，那么这个图就可以缩成一条链。然后判断x和y是否位于度为1的不同的双连通分量中（因为度为1的双连通分量一定位于链的两端）。

AC代码：

#include <bits/stdc++.h>
#define mem(a, v) memset(a, v, sizeof(a))
using namespace std;
const int N = 1e5 + 5;
int n, m, t, k;

struct edge
{
    
    int to, next;
} e[N * 4];
int head[N], ecnt = 0;
void add(int u, int v)
{
    
    e[++ecnt] = {
    v, head[u]};
    head[u] = ecnt;
};

int low[N], dfn[N], cut[N], stk[N], f[N]; // f记录一个点是否位于两端的双连通分量中
int tot = 0, root = 1, top = 0, dcc_cnt = 0;

vector<int> dcc[N], group[N]; // dcc记录双连通分量中有哪些点，group记录一个点位于哪些双连通分量中

void tarjan(int u)
{
    
    low[u] = dfn[u] = ++tot;
    stk[++top] = u;
    int y, cnt = 0; //统计该点连接的双连通分量
    for (int i = head[u]; i; i = e[i].next)
    {
    
        int v = e[i].to;
        if (!dfn[v])
        {
    
            tarjan(v);
            low[u] = min(low[u], low[v]);
            if (dfn[u] <= low[v]) //出现了新的双连通分量
            {
    
                ++cnt, ++dcc_cnt;
                if (u != root) cut[u] = 1;
                while (1)
                {
    
                    y = stk[top--];
                    group[y].push_back(dcc_cnt);
                    dcc[dcc_cnt].push_back(y);
                    if (y == v) //注意这里在遇到v的时候就停止
                    {
    
                        dcc[dcc_cnt].push_back(u);
                        group[u].push_back(dcc_cnt);
                        break;
                    }
                }
            }
        }
        else
            low[u] = min(low[u], dfn[v]);
    }
    if (cnt >= 2 && u == root) cut[root] = 1; //如果根点连接了两个以上的双连通分量，那么根也是割点
}
signed main()
{
    
    ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
    mem(head, 0), mem(f, 0), mem(dfn, 0), mem(cut, 0);

    cin >> n >> m;
    for (int i = 1, u, v; i <= m; i++)
    {
    
        cin >> u >> v;
        add(u, v), add(v, u);
    }

    tarjan(1);

    bool flag = 1;

    for (int i = 1; i <= n && flag; i++) //判断图的连通性
        if (!dfn[i]) flag = 0;

    if (flag && dcc_cnt != 1) //如果图是连通的，并且有不止一个双连通分量，就统计每个双连通分量的度
    {
    
        int idx = 0;
        for (int i = 1; i <= dcc_cnt && flag; i++)
        {
    
            int degree = 0;
            for (auto u : dcc[i])
                if (cut[u]) //只有割点会位于多个双连通分量中，对度有贡献
                    degree += group[u].size() - 1;

            if (degree > 2) flag = 0; //度超过了2，无法构成链
            else if (degree == 1) //度为1，说明位于两端
            {
    
                idx++; //标记两端的双连通分量
                for (auto u : dcc[i])
                    if (!cut[u]) f[u] = idx;
            }
        }
    }
    int q;
    cin >> q;
    while (q--)
    {
    
        int x, y;
        cin >> x >> y;
        if (!flag)
            cout << "NO\n";
        else if (dcc_cnt == 1) //只有一个双连通分量时总是符合的
            cout << "YES\n";
        else
        {
    
            if (f[x] + f[y] == 3) //加起来等于3就一定是位于两端的双连通分量中
                cout << "YES\n";
            else
                cout << "NO\n";
        }
    }
    return 0;
}