当前位置:网站首页>有限与无限只在于一个变量
有限与无限只在于一个变量
2022-08-08 06:22:00 【Upaaui】
设计模式的学习有这么一个版本的变化
版本一
Private Sub Form_Load()
Print 5+6
End Sub
版本二
Private Sub Form_Load()
Dim a As Integer, b As Integer
a = 5
b = 6
Print a + b
End Sub
版本2相对于版本1来说有什么巨大的进步?
我们做软件开发的需要有想象力和创造力,这是需要在学习代码过程中不断的去培养和提高的一个过程。
同样代码,不同的人看到的却是不同的思想,不同的发展与未来。
从版本1到版本2实现了从有限到无限的扩展,从两个确定数相加到两个任意数相加,实现了从有限2个数相加,到无限个数相加。同时通过a+B实现了对算法的封装,从而实现了在这里面具体的加法复用。
边栏推荐
猜你喜欢
“独家全新”MySQL进阶套餐,你确定不看吗?
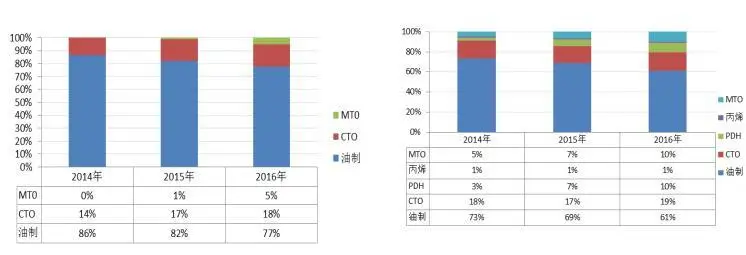
化工行业现状分析:聚烯烃市场消费量近2亿吨
![[WUSTCTF2020]CV Maker1](/img/be/989b1ea8597f31f4b82c2edc6345d5.png)
[WUSTCTF2020]CV Maker1

灯具分析:LED灯预计2028年将达到459亿美元

Sentinel流控规则绑定nacos持久化
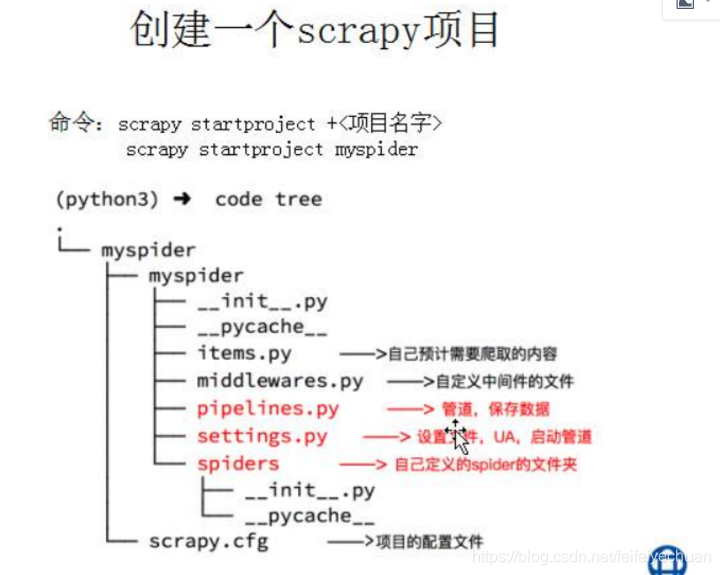
Detailed explanation of Scrapy crawler framework - comprehensive detailed explanation

Plant spice market research: China's market development status and business model analysis in 2022

图像融合简介
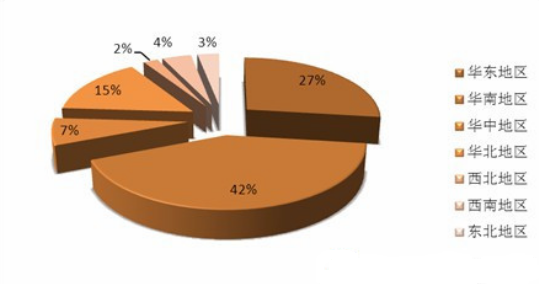
消费品行业报告:化妆品容器市场现状研究分析与发展前景预测

Neo4j服务配置
随机推荐
大恒工业相机搭建双目相机(软件)
基于knn的手写数字识别
AttributeError: ‘GridSearchCV‘ object has no attribute ‘grid_scores_‘
四面拿下字节2-2Offer,入职就是...
leetcode 5 最长回文子串std::pair 和 make_pair运用
摔倒检测综述
500道Golang 常⻅⾯试题⽬解析
[GWCTF 2019]我有一个数据库1
图像评价方法程序-PSNR
redis客户端Jedis/Redisson/Letture对比示例代码
课堂作业--凯撒加密
np.iinfo和 np.finfo的用法
YoloV4训练自己的数据集(三)
四 、TF2.0中张量的数学运算
学生管理系统
Scrapy_Redis distributed processing
数组对象方法
结合实践总结docker 安装 mysql5.7
学习残差神经网络(ResNet)
from sklearn import cross_validation 报错的解决方法