当前位置:网站首页>数据挖掘-06
数据挖掘-06
2022-08-09 12:01:00 【画个圈圈诅咒你 yebo】
最大期望法
最大期望算法(Expectation-Maximization algorithm, EM),或Dempster-Laird-Rubin算法 ,是一类通过迭代进行极大似然估计(Maximum Likelihood Estimation, MLE)的优化算法 ,通常作为牛顿迭代法(Newton-Raphson method)的替代用于对包含隐变量(latent variable)或缺失数据(incomplete-data)的概率模型进行参数估计 。
EM算法的标准计算框架由E步(Expectation-step)和M步(Maximization step)交替组成,算法的收敛性可以确保迭代至少逼近局部极大值 。EM算法是MM算法(Minorize-Maximization algorithm)的特例之一,有多个改进版本,包括使用了贝叶斯推断的EM算法、EM梯度算法、广义EM算法等。
由于迭代规则容易实现并可以灵活考虑隐变量 ,EM算法被广泛应用于处理数据的缺测值,以及很多机器学习(machine learning)算法,包括高斯混合模型(Gaussian Mixture Model, GMM) 和隐马尔可夫模型(Hidden Markov Model, HMM) 的参数估计。
最大似然估计
最大似然其实基本的原理非常简单,假设我们手里现在有一个样本,这个样本服从某种分布,而分布有参数,可如果我现在不知道这个样本分布的具体参数是多少,我们就想要通过抽样得到的样本进行分析,从而估计出一个较准确的相关参数。
以上,这种通过抽样结果反推分布参数的方法就是“最大似然估计”。现在简单思考一下怎么去估计:已知的一个抽样结果和可能的分布(比如说高斯分布),那我就像小学生解方程那样呗,先设出分布的参数(比如高斯分布中就是设出σσ和μμ),然后我计算得到现在这个抽样数据的概率函数,令这个概率最大,看此时相关参数的取值。
这个思路很容易理解,能使得概率最大的参数一定是“最可能”的那个,这里的“最可能”也就是最大似然估计中“最大似然”的真正含义。
只是这么说可能有点抽象,看一个具体的例子。设产品有合格、不合格两类,未知的是不合格品的概率pp,显然这是一个典型的两点分布b(1,p)b(1,p)。我们用随机变量XX表示是否合格,X=0X=0表示合格,X=1X=1表示不合格。如果现在得到了一组抽样数据(x1,x2,…,xn)(x1,x2,…,xn),那么不难写出抽样得到这组数据的概率:
f(X1=x1,X2=x2,…,Xn=xn;p)=∏i=1npxi(1−p)1−xi
f(X1=x1,X2=x2,…,Xn=xn;p)=∏i=1npxi(1−p)1−xi
我们把上面这个联合概率叫做样本的似然函数,一般把它两侧同时取对数(记为对数似然函数L(θ)L(θ))。L(θ)L(θ)关于pp的求偏导数,令偏导数为0,即可求得使得L(p)L(p)最大的pp值。
∂L(p)∂p=0⇒p^=∑i=1nxi/n
∂L(p)∂p=0⇒p^=∑i=1nxi/n
其中,求得的pp值称为pp的最大似然估计,为示区分,用p^p^表示。
其他分布可能计算过程更加复杂,然而基本的步骤与这个例子是一致的。我们总结一下:设总体的概率函数为p(x;θ)p(x;θ),θθ为一个未知的参数,现已知来自总体的一个样本x1,x2,…,xnx1,x2,…,xn那么求取θθ的最大似然估计的步骤如下:
写出似然函数L(θ)L(θ),它实际上就是样本的联合概率函数
L(θ)=p(x1;θ)⋅p(x2;θ)⋅…p(xn;θ)
L(θ)=p(x1;θ)⋅p(x2;θ)⋅…p(xn;θ)
对似然函数求取对数,并整理
ln(L(θ))=lnp(x1;θ)+⋯+lnp(xn;θ)
ln(L(θ))=lnp(x1;θ)+⋯+lnp(xn;θ)
关于参数θθ求偏导,并令偏导数为0,解得参数θ^θ^,这就是参数θθ的最大似然估计
∂L(θ)∂θ=0⇒θ^=…
隐藏变量
上面介绍了最大似然估计,可上面的做法仅适用于不存在隐藏变量的概率模型。什么是隐藏变量呢,我们看这样一个例子。假设现在班上有男女同学若干,同学们的身高是服从正态分布的,当然了,男生身高分布的参数与女生身高分布的参数是不一样的。现在如果给你一个同学的身高,你很难确定这个同学是男是女。如果这个时候抽取样本,让你做上面的最大似然估计,那么就需要做以下两步操作了:
估计一下样本中的每个同学是男生还是女生;
估计男生和女生的身高分布的参数;
第二步就是上面说的最大似然估计,难点在第一步,你还得先猜测男女才行。用更抽象的语言,可以这样描述:属于多个类别的样本混在了一起,不同类别样本的参数不同,现在的任务是从总体中抽样,再通过抽样数据估计每个类别的分布参数。这个描述就是所谓的“在依赖于无法观测的隐藏变量的概率模型中,寻找参数最大似然估计”,隐藏变量在此处就是样本的类别(比如上例中的男女)。这个时候EM算法就派上用场了。
数化后的似然函数
假设对数似然函数如下:
lnL(θ)=ln(p(x1;θ)⋅p(x2;θ)⋅⋯⋅p(xn;θ))=∑i=1nlnp(xi;θ)=∑i=1nln∑j=1mp(xi,z(j);θ)(1)
(1)lnL(θ)=ln(p(x1;θ)⋅p(x2;θ)⋅⋯⋅p(xn;θ))=∑i=1nlnp(xi;θ)=∑i=1nln∑j=1mp(xi,z(j);θ)
公式(1)其实是两步,第一步是对似然函数正常的对数化处理,第二步则把每个p(xi;θ)p(xi;θ)用不同类别的联合分布的概率和表示。可以理解为抽到样本xixi的概率为xixi属于类z(1)z(1)的概率,加上xixi属于类z(2)z(2)的概率,加上。。。一直加到xixi属于类z(m)z(m)的概率。
本质上讲,我们的目的是要求公式(1)的最大值。但是你看,现在(1)中存在对数项里面的加和,如果求导的话,是非常麻烦的,所以,我们首先想到的就是对公式(1)化简,转换其形式。
为了方便推导,我们将xixi对zz的分布函数用Qi(z)Qi(z)表示。那么对于Qi(z)Qi(z),它一定满足如下条件:
∑j=1mQi(z(j))=1, Qi(z(j))≥0
∑j=1mQi(z(j))=1, Qi(z(j))≥0
所以公式(1)可以这样化简:
lnL(θ)=∑i=1nln∑zp(xi,z(j);θ)=∑i=1nln∑j=1mQi(z(j))p(xi,z(j);θ)Qi(z(j))≥∑i=1n∑j=1mQi(z(j))lnp(xi,z(j);θ)Qi(z(j))(2)
(2)lnL(θ)=∑i=1nln∑zp(xi,z(j);θ)=∑i=1nln∑j=1mQi(z(j))p(xi,z(j);θ)Qi(z(j))≥∑i=1n∑j=1mQi(z(j))lnp(xi,z(j);θ)Qi(z(j))
这里的公式(2)非常重要,几乎可以说是整个EM算法的核心公式。可以看到,化简的过程实际上包含了两步,第一是简单的把Qi(z)Qi(z)嵌入,第二则是根据ln()ln()函数是凸函数的性质得到的最后那个 ≥≥ 的结果。关于凸函数,我会在本文4.2节中详细说。先看看这个式子,我们发现,通过化简,其实是求得了似然函数的一个下界(记为J(z,Q)J(z,Q)):
J(z,Q)=∑i=1n∑j=1mQi(z(j))lnp(xi,z(j);θ)Qi(z(j))
J(z,Q)=∑i=1n∑j=1mQi(z(j))lnp(xi,z(j);θ)Qi(z(j))
这个J(z,Q)J(z,Q)其实就是变量p(xi,z(j);θ)Qi(z(j))p(xi,z(j);θ)Qi(z(j))的期望。回忆一下期望的算法是E(X)=∑xp(x)E(X)=∑xp(x),这里Qi(z(j))Qi(z(j))相当于是概率。
我们发现,J(z,Q)J(z,Q)是比较容易求导的(因为是一个简单的加法式子),但现在的问题在于对下界求导没用,我们要对似然函数求导才行。换个思路想想,下界取决于p(xi,z(j);θ)p(xi,z(j);θ)和Qi(z(j))Qi(z(j)),我们如果能通过这两个值不断提升下界,使之不断逼近似然函数ln L(θ)ln L(θ),在某种情况下,如果J(z,Q)=ln L(θ)J(z,Q)=ln L(θ),那就大功告成了。说到这,先暂停,我们看一下凸函数的定义和性质。
EM算法的收敛性证明
但是我们写到这里还有一个疑问,这种反复迭代一定会收敛吗?假定θ(t)θ(t)和θ(t+1)θ(t+1)为第tt轮和第t+1t+1轮迭代后的结果,l(θ(t))l(θ(t))和l(θ(t+1))l(θ(t+1))为对应的似然函数。显然,如果l(θ(t))≤l(θ(t+1))l(θ(t))≤l(θ(t+1)),那么随着迭代次数的增加,最终会一步步逼近最大似然值。也就是说,只需要证明公式(6)成立即可。
l(θ(t))<l(θ(t+1))(6)
(6)l(θ(t))<l(θ(t+1))
证明:得到θ(t)θ(t)后,执行E步:
Qti(z(j))=p(z(j)|xi;θt)
Qit(z(j))=p(z(j)|xi;θt)
此时,
l(θ(t))=∑i=1n∑j=1mQi(z(j))lnp(xi,z(j);θt))Qi(z(j))
l(θ(t))=∑i=1n∑j=1mQi(z(j))lnp(xi,z(j);θt))Qi(z(j))
然后执行M步,求偏导为0,得到θ(t+1)θ(t+1),此时有公式(7)成立:
l(θ(t+1))≥∑i=1n∑j=1mQi(z(j))lnp(xi,z(j);θ(t+1)))Qi(z(j))≥∑i=1n∑j=1mQi(z(j))lnp(xi,z(j);θt))Qi(z(j))=l(θt)(7)
(7)l(θ(t+1))≥∑i=1n∑j=1mQi(z(j))lnp(xi,z(j);θ(t+1)))Qi(z(j))≥∑i=1n∑j=1mQi(z(j))lnp(xi,z(j);θt))Qi(z(j))=l(θt)
简单说一下公式(7),第一步l(θ(t+1))≥∑ni=1∑mj=1Qi(z(j))lnp(xi,z(j);θ(t+1))Qi(z(j))l(θ(t+1))≥∑i=1n∑j=1mQi(z(j))lnp(xi,z(j);θ(t+1))Qi(z(j))是由前面的公式(2)决定的;
第二步 ≥∑ni=1∑mj=1Qi(z(j))lnp(xi,z(j);θt))Qi(z(j))≥∑i=1n∑j=1mQi(z(j))lnp(xi,z(j);θt))Qi(z(j))是M步的定义,M步中,将θtθt调整到θ(t+1)θ(t+1)就是为了使似然函数l(θ(t+1))l(θ(t+1))最大化。
综上,我们证明了EM算法的收敛性。
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets
from sklearn.mixture import GaussianMixture
from sklearn.model_selection import StratifiedKFold
colors = ['navy', 'turquoise', 'darkorange']
def make_ellipses(gmm, ax):
for n, color in enumerate(colors):
if gmm.covariance_type == 'full':
covariances = gmm.covariances_[n][:2, :2]
elif gmm.covariance_type == 'tied':
covariances = gmm.covariances_[:2, :2]
elif gmm.covariance_type == 'diag':
covariances = np.diag(gmm.covariances_[n][:2])
elif gmm.covariance_type == 'spherical':
covariances = np.eye(gmm.means_.shape[1]) * gmm.covariances_[n]
v, w = np.linalg.eigh(covariances)
u = w[0] / np.linalg.norm(w[0])
angle = np.arctan2(u[1], u[0])
angle = 180 * angle / np.pi # convert to degrees
v = 2. * np.sqrt(2.) * np.sqrt(v)
ell = mpl.patches.Ellipse(gmm.means_[n, :2], v[0], v[1],
180 + angle, color=color)
ell.set_clip_box(ax.bbox)
ell.set_alpha(0.5)
ax.add_artist(ell)
iris = datasets.load_iris()
# Break up the dataset into non-overlapping training (75%)
# and testing (25%) sets.
skf = StratifiedKFold(n_splits=4)
# Only take the first fold.
train_index, test_index = next(iter(skf.split(iris.data, iris.target)))
X_train = iris.data[train_index]
y_train = iris.target[train_index]
X_test = iris.data[test_index]
y_test = iris.target[test_index]
n_classes = len(np.unique(y_train))
# Try GMMs using different types of covariances.
estimators = dict((cov_type, GaussianMixture(n_components=n_classes,
covariance_type=cov_type, max_iter=20, random_state=0))
for cov_type in ['spherical', 'diag', 'tied', 'full'])
n_estimators = len(estimators)
plt.figure(figsize=(3 * n_estimators // 2, 6))
plt.subplots_adjust(bottom=.01, top=0.95, hspace=.15, wspace=.05,
left=.01, right=.99)
for index, (name, estimator) in enumerate(estimators.items()):
# Since we have class labels for the training data, we can
# initialize the GMM parameters in a supervised manner.
estimator.means_init = np.array([X_train[y_train == i].mean(axis=0)
for i in range(n_classes)])
# Train the other parameters using the EM algorithm.
estimator.fit(X_train)
h = plt.subplot(2, n_estimators // 2, index + 1)
make_ellipses(estimator, h)
for n, color in enumerate(colors):
data = iris.data[iris.target == n]
plt.scatter(data[:, 0], data[:, 1], s=0.8, color=color,
label=iris.target_names[n])
# Plot the test data with crosses
for n, color in enumerate(colors):
data = X_test[y_test == n]
plt.scatter(data[:, 0], data[:, 1], marker='x', color=color)
y_train_pred = estimator.predict(X_train)
train_accuracy = np.mean(y_train_pred.ravel() == y_train.ravel()) * 100
plt.text(0.05, 0.9, 'Train accuracy: %.1f' % train_accuracy,
transform=h.transAxes)
y_test_pred = estimator.predict(X_test)
test_accuracy = np.mean(y_test_pred.ravel() == y_test.ravel()) * 100
plt.text(0.05, 0.8, 'Test accuracy: %.1f' % test_accuracy,
transform=h.transAxes)
plt.xticks(())
plt.yticks(())
plt.title(name)
plt.legend(scatterpoints=1, loc='lower right', prop=dict(size=12))
plt.show()
边栏推荐
- Two minutes recording can pass by second language!The volcano how to practice and become voice tone reproduction technology?
- Batch大小不一定是2的n次幂!ML资深学者最新结论
- 鹅厂机器狗花式穿越10m梅花桩:前空翻、单桩跳、起身作揖...全程不打一个趔趄...
- ThreadLocal的简单理解
- Apexsqlrecover cannot connect to database
- OpenSSF的开源软件风险评估工具:Scorecards
- 推荐一个免费50时长的AI算力平台
- AQS同步组件-FutureTask解析和用例
- FFmpeg在win10上编译安装(配置libx264)
- h264协议
猜你喜欢
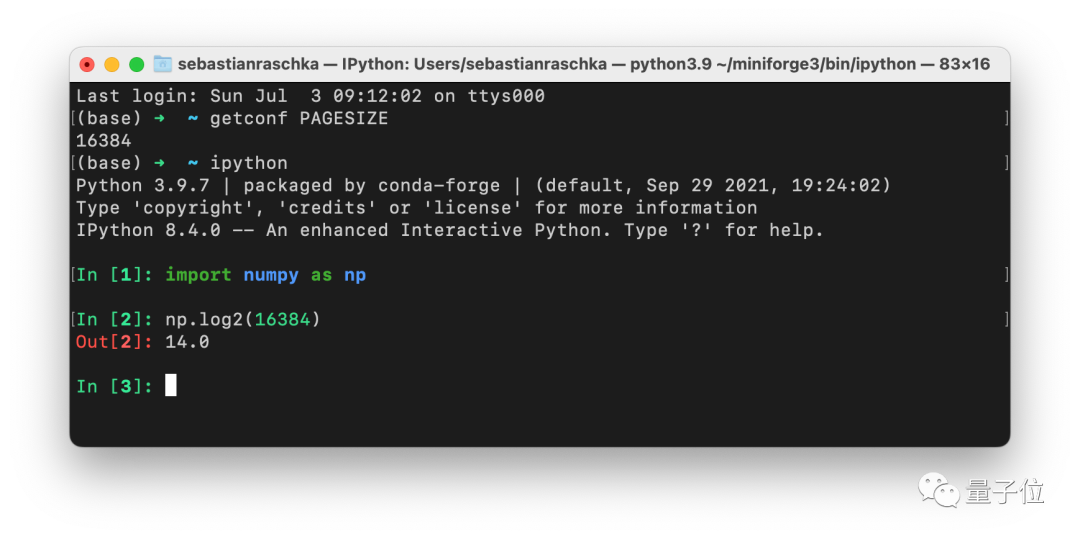
The batch size does not have to be a power of 2!The latest conclusions of senior ML scholars

1-hour live broadcast recruitment order: industry big names share dry goods, and enterprise registration opens丨qubit·viewpoint
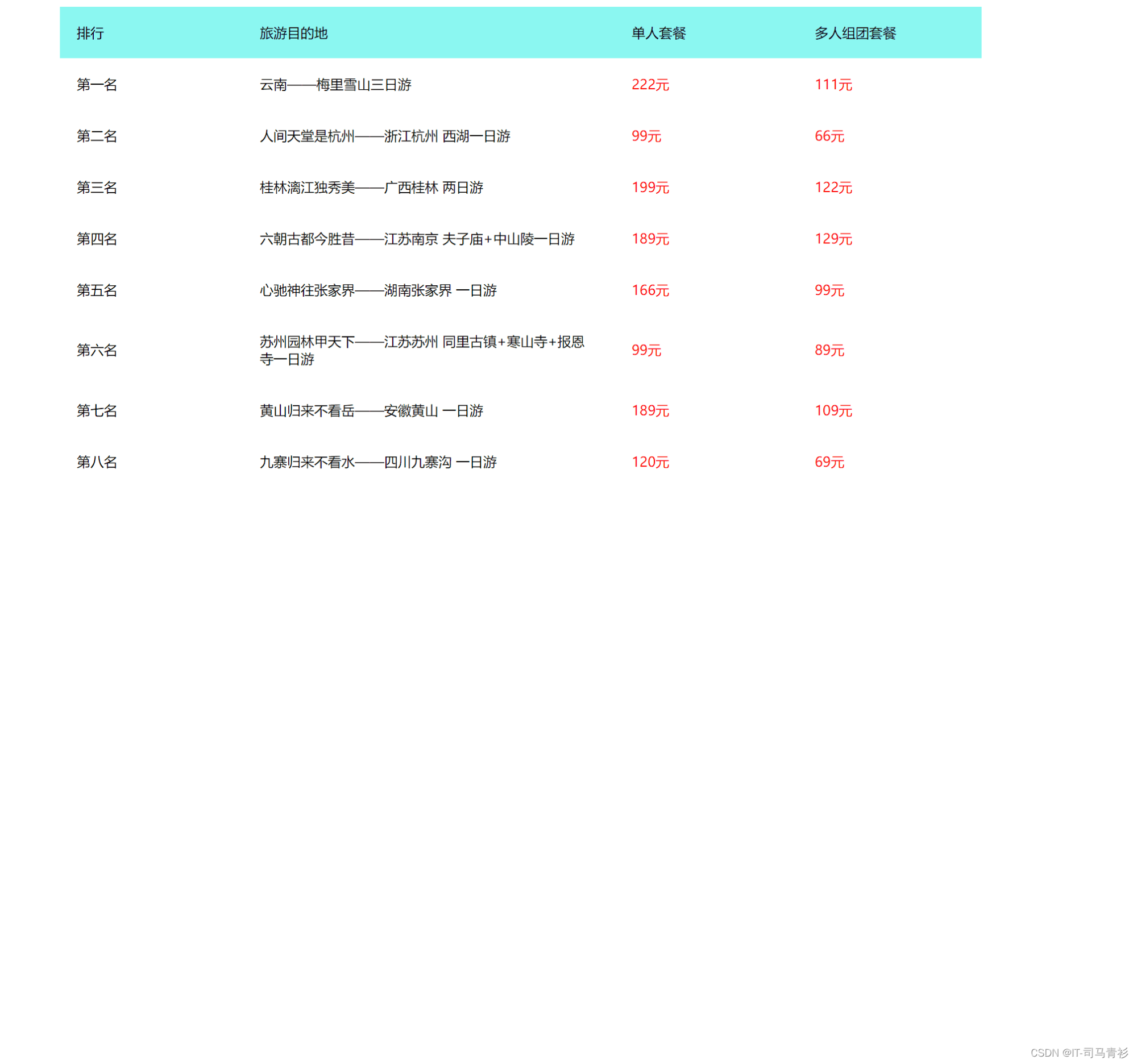
web course design
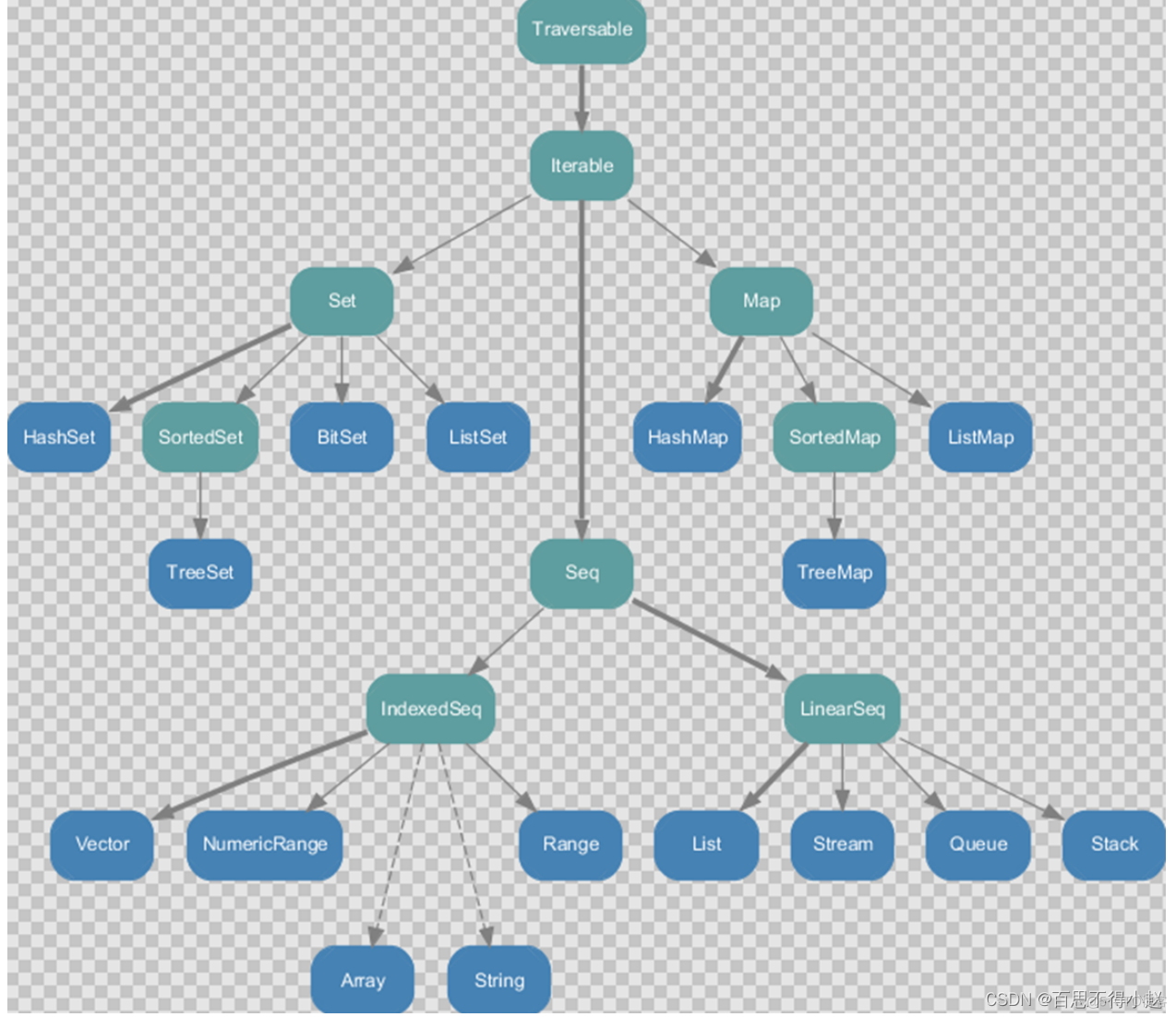
Scala 高阶(七):集合内容汇总(上篇)
#物联网征文#小熊派设备开发实战

2022牛客多校(六)M. Z-Game on grid

Two minutes recording can pass by second language!The volcano how to practice and become voice tone reproduction technology?
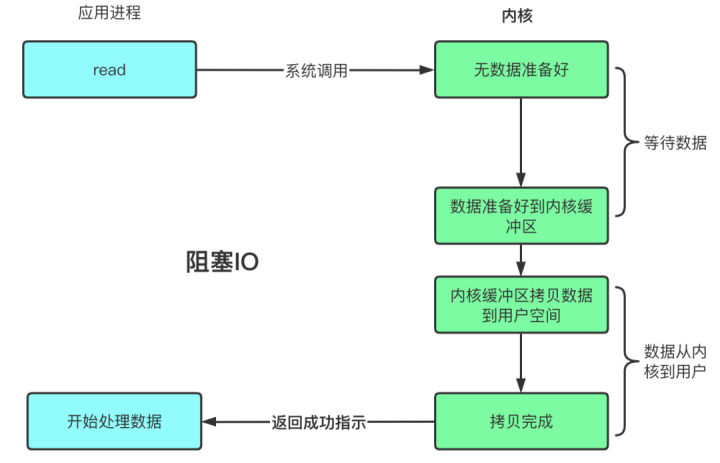
阻塞、非阻塞、多路复用、同步、异步、BIO、NIO、AIO 一锅端

26、管道参数替换命令xargs
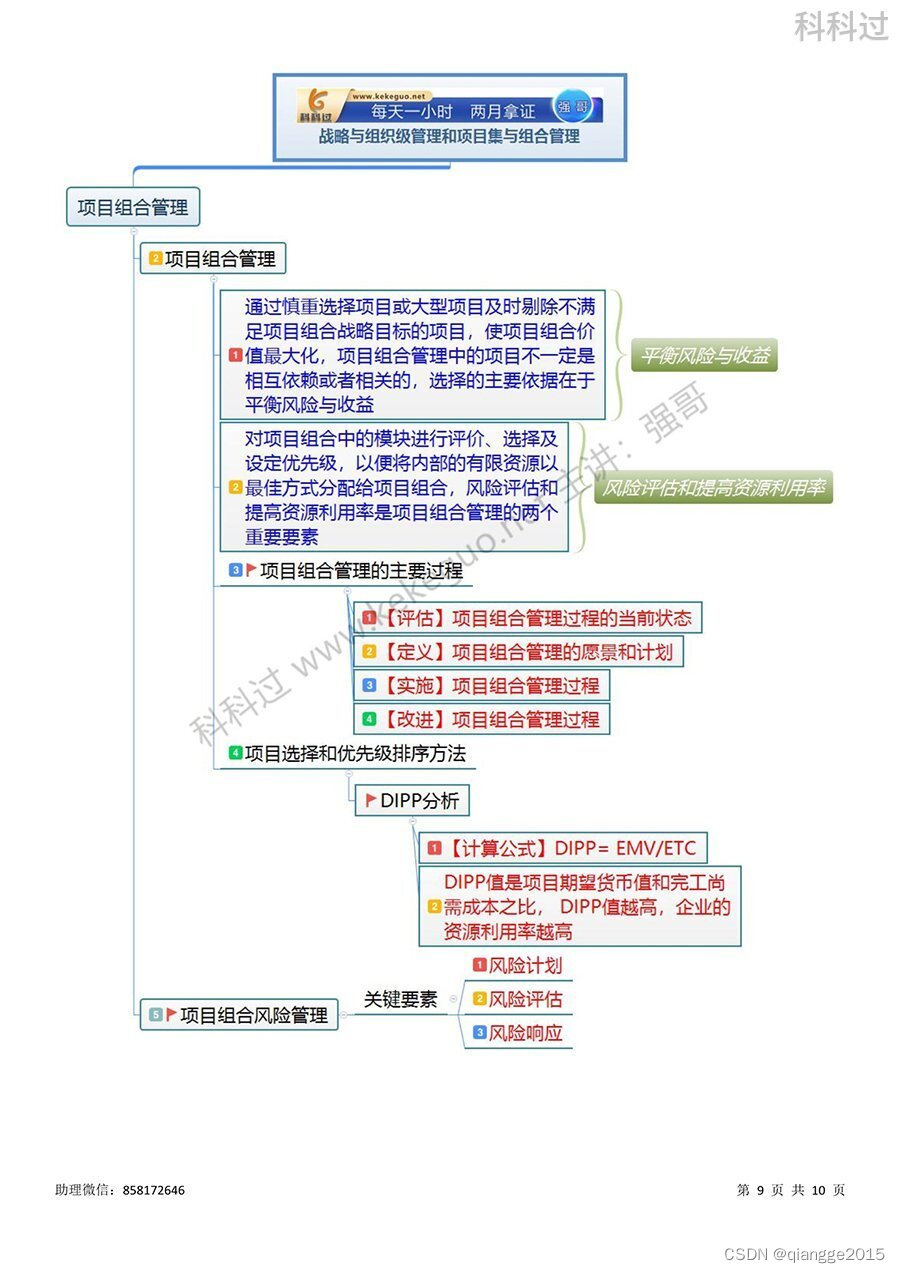
信息系统项目管理师必背核心考点(六十三)项目组合管理的主要过程&DIPP分析
随机推荐
软件测试——金融测试类面试题,看完直接去面试了
无需精子卵子子宫体外培育胚胎,Cell论文作者这番话让网友们炸了
荣耀携手Blue Yonder,加快企业战略增长
Reading and writing after separation, performance were up 100%
Win10 compiles the x264 library (there are also generated lib files)
IDEA close/open reference prompt Usages
Information system project managers must memorize the core test sites (63) The main process of project portfolio management & DIPP analysis
Django cannot link mysql database
The batch size does not have to be a power of 2!The latest conclusions of senior ML scholars
Two minutes recording can pass by second language!The volcano how to practice and become voice tone reproduction technology?
Ways to prevent data fraud
阿里云新增三大高性能计算解决方案,助力生命科学行业快速发展
Senior told me that the giant MySQL is through SSH connection
proto3-2 syntax
放下手机吧:实验表明花20分钟思考和上网冲浪同样快乐
已解决IndentationError: unindent does not match any oute r indentation Level
【小程序】低代码+小游戏=小游戏可视化开发
脱光衣服待着就能减肥,当真有这好事?
The FFmpeg library is configured and used on win10 (libx264 is not configured)
How to upload local file trial version in binary mode in ABAP report