当前位置:网站首页>HDU-Tunnel Warfare
HDU-Tunnel Warfare
2022-04-23 05:51:00 【Round moon】
Tunnel Warfare
题目描述
During the War of Resistance Against Japan, tunnel warfare was carried out extensively in the vast areas of north China Plain. Generally speaking, villages connected by tunnels lay in a line. Except the two at the ends, every village was directly connected with two neighboring ones.
Frequently the invaders launched attack on some of the villages and destroyed the parts of tunnels in them. The Eighth Route Army commanders requested the latest connection state of the tunnels and villages. If some villages are severely isolated, restoration of connection must be done immediately!
输入描述
The first line of the input contains two positive integers n and m (n, m ≤ 50,000) indicating the number of villages and events. Each of the next m lines describes an event.
There are three different events described in different format shown below:
D x: The x-th village was destroyed.
Q x: The Army commands requested the number of villages that x-th village was directly or indirectly connected with including itself.
R: The village destroyed last was rebuilt.
输出描述
Output the answer to each of the Army commanders’ request in order on a separate line.
Sample Input
7 9
D 3
D 6
D 5
Q 4
Q 5
R
Q 4
R
Q 4
Sample Output
1
0
2
4
题目大意
一段列表,选中的点被摧毁D。查询Q选中的点所在连续区间的长度。R恢复最后一个被摧毁的点。
不需要考虑重复摧毁
样例解释
经过三轮摧毁,3,6,5被摧毁。4号位置连续长度为1

5号位置被摧毁,长度为0
恢复最后一个被摧毁的5点。4号位置的连续长度为2

恢复最后一个被摧毁的点6。4号位置的连续长度为4

思路解析(思路一,思路二)
本题用两种思路去解题,第一种思路,维护区间最大值和最小值的方法去解决。第二种思路,线段树的区间合并方法去解决。
思路一
我们把被摧毁的点设置为自己的id值,如果没被摧毁就设置为很大的一个数字。这样我们就能知道从自己包括自己的点到自己最右侧的最小值就是自己的右边界。

这里发现最小值是5
如果把没被摧毁的设置为一个很小的值,那么从自己包括自己到最左侧的最大值就是自己的左边界。

这里发现最大值是3
那么中间的长度就是5-3-1
这里需要特殊的判定一下,如果这两个值的值重复了,那么就是0
我们这里的很大的值设为长度+1,很小的值就是0,这样我们就能把整个区间给包括起来了。
AC代码
//#include<unordered_map>
#include<algorithm>
#include<iostream>
#include<string.h>
#include <iomanip>
#include<stdio.h>
#include<vector>
#include<string>
#include<math.h>
#include<cmath>
#include<queue>
#include<stack>
#include<deque>
#include<map>
#include<set>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const ll ll_inf = 9223372036854775807;
const int int_inf = 2147483647;
const short short_inf = 32767;
const ll less_inf = 0x3f3f3f3f;
const char char_inf = 127;
#pragma GCC optimize(2)
#define accelerate cin.tie(NULL);cout.tie(NULL);ios::sync_with_stdio(false);
#define PI 3.141592653589793
#define EPS 1.0e-8
ll gcd(ll a, ll b) {
return b ? gcd(b, a % b) : a;
}
ll lcm(ll a, ll b) {
return a * b / gcd(a, b);
}
inline ll read() {
ll c = getchar(), Nig = 1, x = 0;
while (!isdigit(c) && c != '-')c = getchar();
if (c == '-')Nig = -1, c = getchar();
while (isdigit(c))x = ((x << 1) + (x << 3)) + (c ^ '0'), c = getchar();
return Nig * x;
}
inline void out(ll a) {
if (a < 0)putchar('-'), a = -a;
if (a > 9)out(a / 10);
putchar(a % 10 + '0');
}
ll qpow(ll x, ll n, ll mod) {
ll res = 1;
while (n > 0) {
if (n & 1)res = (res * x) % mod;
x = (x * x) % mod;
n >>= 1;
}
return res;
}
#define read read()
const int N = 50000;
struct node
{
int maxn, minn;
}tree[N * 4 + 7];
int n, m;
void push_up(int rt)
{
tree[rt].maxn = max(tree[rt << 1].maxn, tree[rt << 1 | 1].maxn);
tree[rt].minn = min(tree[rt << 1].minn, tree[rt << 1 | 1].minn);
}
void creat(int l, int r, int rt)
{
if (l == r)
{
tree[rt].maxn =0;
tree[rt].minn = n+1;
return;
}
int mid = l + r >> 1;
creat(l, mid, rt << 1);
creat(mid + 1, r, rt << 1 | 1);
push_up(rt);
}
void updata(int pos, int maxn, int minn, int l, int r, int rt)
{
if (l == r)
{
tree[rt].maxn = maxn;
tree[rt].minn = minn;
return;
}
int mid = l + r >> 1;
if (pos <= mid)updata(pos, maxn, minn, l, mid, rt << 1);
else updata(pos, maxn, minn, mid + 1, r, rt << 1 | 1);
push_up(rt);
}
node query(int L, int R, int l, int r, int rt)
{
node temp;
int maxn = -int_inf;
int minn = int_inf;
if (L <= l && r <= R)
{
temp.maxn = tree[rt].maxn;
temp.minn = tree[rt].minn;
return temp;
}
int mid = l + r >> 1;
if (L <= mid) {
temp = query(L, R, l, mid, rt << 1);
maxn = max(maxn, temp.maxn);
minn = min(minn, temp.minn);
}
if (R > mid) {
temp = query(L, R, mid + 1, r, rt << 1 | 1);
maxn = max(maxn, temp.maxn);
minn = min(minn, temp.minn);
}
return node{
maxn,minn };
}
stack<int>s;
int main()
{
while (scanf("%d%d", &n, &m) != EOF)
{
while (!s.empty())s.pop();
creat(1, n, 1);
while (m--)
{
char mark[3];
scanf("%s", mark);
if (mark[0] == 'D')
{
int id;
scanf("%d", &id);
updata(id, id, id, 1, n, 1);
s.push(id);
}
else if (mark[0] == 'Q')
{
int id;
scanf("%d", &id);
node left = query(1, id, 1, n, 1);
node right = query(id, n, 1, n, 1);
if (right.minn == left.maxn)puts("0");
else printf("%d\n", right.minn - left.maxn - 1);
}
else
{
int id = s.top();
s.pop();
updata(id, 0, n + 1, 1, n, 1);
}
}
}
}
思路二
我们利用区间合并的方法,去单点修改每一个点。在查询的时候,我们判断当前要查寻的点是不是位于组合成的区间内,如果是,在递归一半区间的时候要注意把另一半的区间也要递归下去。详情见代码
AC代码
//#include<unordered_map>
#include<algorithm>
#include<iostream>
#include<string.h>
#include <iomanip>
#include<stdio.h>
#include<vector>
#include<string>
#include<math.h>
#include<cmath>
#include<queue>
#include<stack>
#include<deque>
#include<map>
#include<set>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const ll ll_inf = 9223372036854775807;
const int int_inf = 2147483647;
const short short_inf = 32767;
const ll less_inf = 0x3f3f3f3f;
const char char_inf = 127;
#pragma GCC optimize(2)
#define accelerate cin.tie(NULL);cout.tie(NULL);ios::sync_with_stdio(false);
#define PI 3.141592653589793
#define EPS 1.0e-8
ll gcd(ll a, ll b) {
return b ? gcd(b, a % b) : a;
}
ll lcm(ll a, ll b) {
return a * b / gcd(a, b);
}
inline ll read() {
ll c = getchar(), Nig = 1, x = 0;
while (!isdigit(c) && c != '-')c = getchar();
if (c == '-')Nig = -1, c = getchar();
while (isdigit(c))x = ((x << 1) + (x << 3)) + (c ^ '0'), c = getchar();
return Nig * x;
}
inline void out(ll a) {
if (a < 0)putchar('-'), a = -a;
if (a > 9)out(a / 10);
putchar(a % 10 + '0');
}
ll qpow(ll x, ll n, ll mod) {
ll res = 1;
while (n > 0) {
if (n & 1)res = (res * x) % mod;
x = (x * x) % mod;
n >>= 1;
}
return res;
}
#define read read()
const int N = 50000;
struct node
{
int len, maxn, lmaxn, rmaxn;
}tree[N * 4 + 7];
void push_up(int rt)
{
if (tree[rt << 1].lmaxn == tree[rt << 1].len)
tree[rt].lmaxn = tree[rt << 1].maxn + tree[rt << 1 | 1].lmaxn;
else
tree[rt].lmaxn = tree[rt << 1].lmaxn;
if (tree[rt << 1 | 1].rmaxn == tree[rt << 1 | 1].len)
tree[rt].rmaxn = tree[rt << 1].rmaxn + tree[rt << 1 | 1].maxn;
else
tree[rt].rmaxn = tree[rt << 1 | 1].rmaxn;
tree[rt].maxn = max(tree[rt << 1].rmaxn + tree[rt << 1 | 1].lmaxn, max(tree[rt << 1].maxn, tree[rt << 1 | 1].maxn));
}
void creat(int l, int r, int rt)
{
tree[rt].len = r - l + 1;
if (l == r)
{
tree[rt].rmaxn = tree[rt].lmaxn = tree[rt].maxn = 1;
return;
}
int mid = l + r >> 1;
creat(l, mid, rt << 1);
creat(mid + 1, r, rt << 1 | 1);
push_up(rt);
}
void update(int pos, int mark, int l, int r, int rt)
{
if (l == r)
{
tree[rt].lmaxn = tree[rt].rmaxn = tree[rt].maxn = mark;
return;
}
int mid = l + r >> 1;
if (pos <= mid)update(pos, mark, l, mid, rt << 1);
else update(pos, mark, mid + 1, r, rt << 1 | 1);
push_up(rt);
}
int query(int pos, int l, int r, int rt)
{
int mid = l + r >> 1;
if (l == r || tree[rt].maxn == 0 || tree[rt].maxn == tree[rt].len)
return tree[rt].maxn;
if (pos <= mid)
{
if (pos >= mid - tree[rt << 1].rmaxn + 1)
return query(pos, l, mid, rt << 1) + query(mid + 1, mid + 1, r, rt << 1 | 1);
else
return query(pos, l, mid, rt << 1);
}
else
{
if (pos <= mid + tree[rt << 1 | 1].lmaxn)
return query(mid, l, mid, rt << 1) + query(pos, mid + 1, r, rt << 1 | 1);
else return query(pos, mid + 1, r, rt << 1 | 1);
}
}
stack<int>s;
int main()
{
int n, m;
while (~scanf("%d%d", &n, &m))
{
while (!s.empty())s.pop();
memset(tree, 0, sizeof(tree));
creat(1, n, 1);
while (m--)
{
char Str[5];
scanf("%s", Str);
if (Str[0] == 'D')
{
int id = read;
s.push(id);
update(id, 0, 1, n, 1);
}
else if (Str[0] == 'R')
{
int id = s.top();
s.pop();
update(id, 1, 1, n, 1);
}
else
{
int id = read;
int len = query(id, 1, n, 1);
out(len);
puts("");
}
}
}
}
By-Round Moon
版权声明
本文为[Round moon]所创,转载请带上原文链接,感谢
https://blog.csdn.net/qq_35339563/article/details/119970721
边栏推荐
猜你喜欢

PN结、二极管原理详解与应用

Introduction to nonparametric camera distortion model

【UDS统一诊断服务】四、诊断典型服务(5)— 功能/元件测试功能单元(例行程序功能单元0x31)

基于VGG卷积神经网络的图像识别代码实现

QT icon application
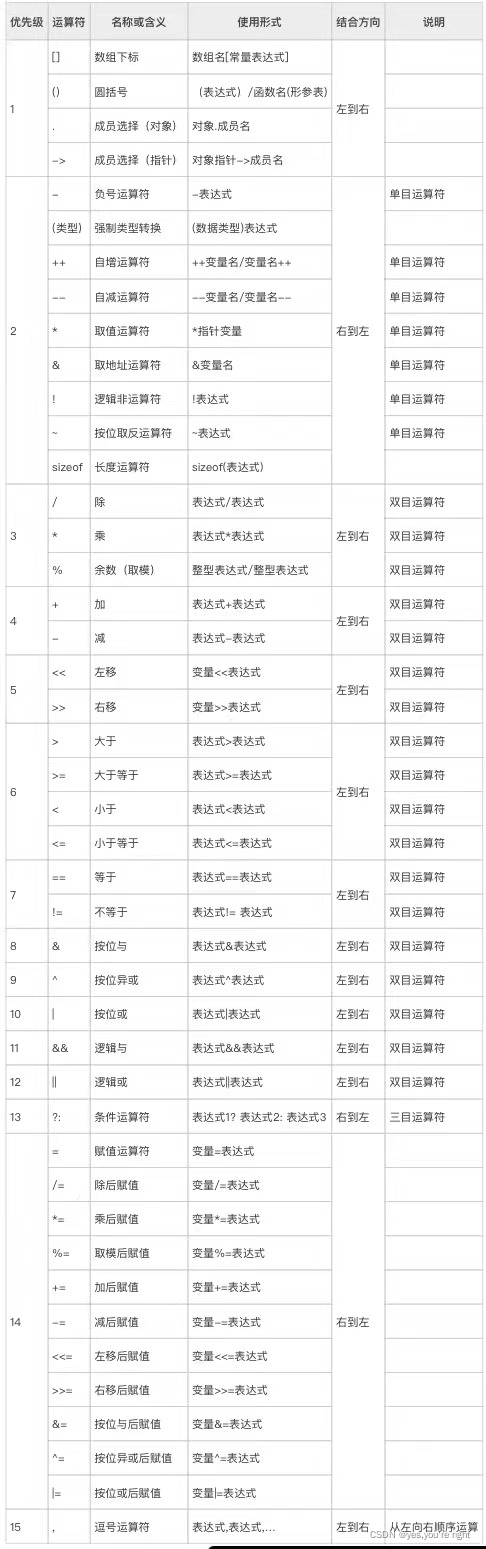
C语言的运算符
![[UDS unified diagnostic service] III. application layer protocol (1)](/img/e7/813e29a30e08eb92ccc836743be9aa.png)
[UDS unified diagnostic service] III. application layer protocol (1)

File viewing commands and user management commands
![[untitled]](/img/03/0ece1ea11558b9b6dd0644bb508987.png)
[untitled]

基于SSD的物体检测案例实现
随机推荐
Shell脚本 单引号、双引号和反引号的区别
【UDS统一诊断服务】(补充)五、ECU bootloader开发要点详解 (1)
带默认模板实参的类模板与模板模板形参的匹配
[UDS unified diagnosis service] i. diagnosis overview (2) - main diagnosis protocols (K-line and can)
Static member
TensorFlow张量介绍
C语言中volatile的使用
客户端软件增量更新
浮点数双精度,单精度以及半精度知识总结
【UDS统一诊断服务】四、诊断典型服务(4)— 在线编程功能单元(0x34-0x38)
【UDS统一诊断服务】三、应用层协议(2)
cv_bridge 与opencv 版本不匹配的解决
gcc ,g++,gdb的安装
Qt 添加QSerialPort类 实现串口操作
Qt 给应用程序加图标
[UDS unified diagnostic service] II. Network layer protocol (2) - data transmission rules (single frame and multi frame)
File viewing commands and user management commands
Matlab calibration board corner detection principle
sqlite编译
修改注册表的值