当前位置:网站首页>压缩映射定理
压缩映射定理
2022-04-23 14:27:00 【patrickpdx】
定义
设 X X X 为距离空间, T : X → X T: X \rightarrow X T:X→X 是一映射,若存在 0 ≤ λ < 1 0\leq \lambda<1 0≤λ<1,使得
d ( T x , T y ) ≤ λ d ( x , y ) , ∀ x , y ∈ X d(Tx,Ty)\leq \lambda d(x,y), \quad \forall x,y\in X d(Tx,Ty)≤λd(x,y),∀x,y∈X
则称 T T T 是压缩的
引理
压缩映射是连续的
若 x n → x x_{n} \rightarrow x xn→x,则: T x n → T x Tx_{n}\rightarrow Tx Txn→Tx
证明:
d ( T x n , T x ) ≤ λ d ( x n , x ) → 0 d(Tx_{n}, Tx) \leq \lambda d(x_{n},x) \rightarrow 0 d(Txn,Tx)≤λd(xn,x)→0
压缩映射定理
完备距离空间上的压缩映射存在唯一的不动点
证明:
设 X X X 为任意完备距离空间, T T T 是 X X X 上的压缩映射. 任取 x 0 ∈ X x_{0} \in X x0∈X,下面证明数列 { x n } \{x_{n}\} {
xn} :
x n = T x n − 1 x_{n} = T x_{n-1} xn=Txn−1
的极限 x = lim n → ∞ x n x = \lim\limits_{n\rightarrow \infty}x_{n} x=n→∞limxn 存在,且为不动点
(1) 首先证明 { x n } \{x_{n}\} {
xn} 是 Cauchy 序列:
d ( x n + 1 , x n ) = d ( T x n , T x n − 1 ) ≤ λ d ( x n , x n − 1 ) d(x_{n+1},x_{n}) = d(Tx_{n},Tx_{n-1})\leq \lambda d(x_{n},x_{n-1}) d(xn+1,xn)=d(Txn,Txn−1)≤λd(xn,xn−1)
进而
d ( x n + 1 , x n ) ≤ λ n d ( x 1 , x 0 ) d(x_{n+1},x_{n})\leq \lambda^{n}d(x_{1},x_{0}) d(xn+1,xn)≤λnd(x1,x0)
对于任何正整数 n n n 和 p p p :
KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲ d(x_{n+p},x_{n…
因此对于 ∀ ϵ > 0 \forall \epsilon>0 ∀ϵ>0, ∃ N \exists N ∃N,使得当 n > N n>N n>N 时,对 ∀ p \forall p ∀p 满足:
∣ d ( x n + p , x n ) ∣ ≤ ϵ |d(x_{n+p},x_{n})|\leq \epsilon ∣d(xn+p,xn)∣≤ϵ
(2) 因为空间 X X X 是完备的,因此 { x n } \{x_{n}\} { xn} 收敛
(3) 进而 x = lim n → ∞ x n = lim n → ∞ T x n − 1 = T lim n → ∞ x n − 1 = T x x=\lim\limits_{n\rightarrow \infty}x_{n} = \lim\limits_{n\rightarrow \infty} Tx_{n-1} = T \lim\limits_{n\rightarrow \infty}x_{n-1} = Tx x=n→∞limxn=n→∞limTxn−1=Tn→∞limxn−1=Tx
版权声明
本文为[patrickpdx]所创,转载请带上原文链接,感谢
https://blog.csdn.net/Jinyindao243052/article/details/124213732
边栏推荐
- ASEMI超快恢复二极管与肖特基二极管可以互换吗
- Use of ansible and common modules
- 51单片机+LCD12864液晶显示的俄罗斯方块游戏,Proteus仿真、AD原理图、代码、论文等
- IE8 browser prompts whether to block access to JS script
- flannel 原理 之 子网划分
- setcontext getcontext makecontext swapcontext
- 解决ssh配置文件优化以及连接慢的问题
- TLS/SSL 协议详解 (30) SSL中的RSA、DHE、ECDHE、ECDH流程与区别
- ArrayList collection basic usage
- Gif to still image processing
猜你喜欢

Find daffodils - for loop practice
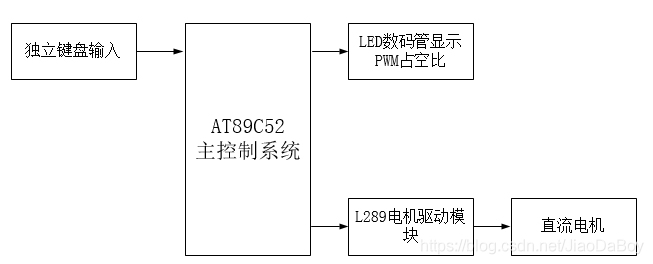
PWM speed regulation control system of DC motor based on 51 single chip microcomputer (with complete set of data such as Proteus simulation + C program)
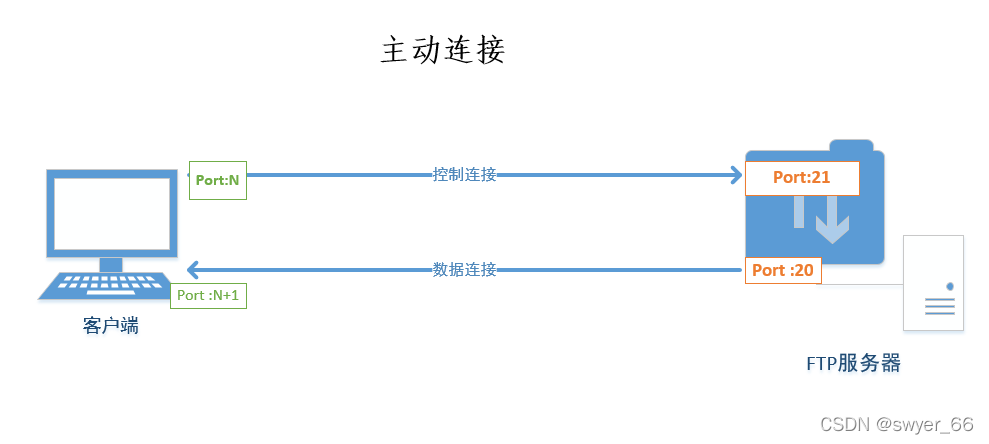
常见存储类型和FTP主被动模式解析
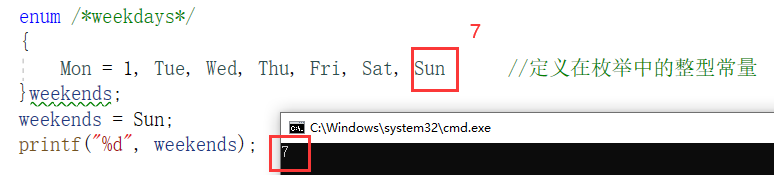
C语言知识点精细详解——数据类型和变量【2】——整型变量与常量【1】

AT89C52单片机的频率计(1HZ~20MHZ)设计,LCD1602显示,含仿真、原理图、PCB与代码等
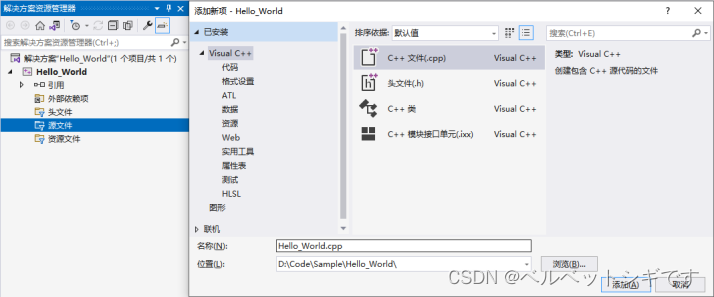
C语言知识点精细详解——初识C语言【1】
51单片机+LCD12864液晶显示的俄罗斯方块游戏,Proteus仿真、AD原理图、代码、论文等

ASEMI整流模块MDQ100-16在智能开关电源中的作用

51 MCU + LCD12864 LCD Tetris game, proteus simulation, ad schematic diagram, code, thesis, etc

ASEMI超快恢复二极管与肖特基二极管可以互换吗
随机推荐
交通灯系统51单片机设计(附Proteus仿真、C程序、原理图及PCB、论文等全套资料)
Wechat applet rotation map swiper
初始c语言大致框架适合复习和初步认识
拼接hql时,新增字段没有出现在构造方法中
PWM speed regulation control system of DC motor based on 51 single chip microcomputer (with complete set of data such as Proteus simulation + C program)
Mq-2 and DS18B20 fire temperature smoke alarm system design, 51 single chip microcomputer, with simulation, C code, schematic diagram, PCB, etc
外包干了四年,废了...
一篇博客让你学会在vscode上编写markdown
AT89C51 MCU digital voltmeter development, measuring range 0 ~ 5V, proteus simulation, schematic diagram, PCB and C program, etc
QT actual combat: Yunxi calendar
Tongxin UOS uninstall php7 2.24, install php7 4.27 ; Uninstall and then install PHP 7.2.34
source insight via samba
Detailed explanation of C language knowledge points -- first knowledge of C language [1]
OpenSSH的升级、版本号的修改
source insight via samba
API Gateway/API 网关(三) - Kong的使用 - 限流rate limiting(redis)
Matlab Simulink modeling and design of single-phase AC-AC frequency converter, with MATLAB simulation, PPT and papers
8.3 语言模型与数据集
LLVM - 生成for循环
JS format time