Camera imaging + homography transformation + camera calibration + stereo correction

1. Camera model

Reference resources ： Research on Key Technologies of intelligent robot target grasping – Thank you Harbin Engineering University Doctoral Dissertation
pinhole imaging , Directly above ：

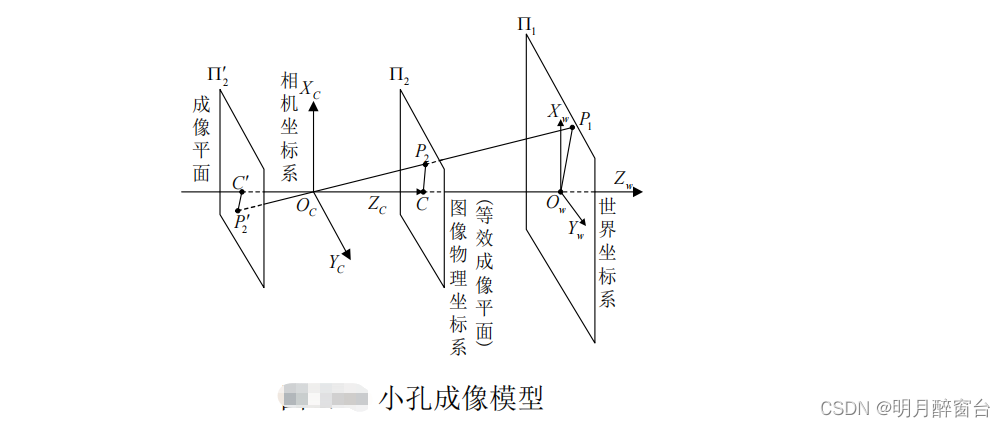
The camera coordinate system and image pixel coordinate system are established to describe the relationship between spatial coordinates and image coordinates . The camera coordinate system takes the center point of the optical axis of the camera as the origin , Take the optical axis as the direction Z Axis , The pixel coordinates of the image are represented by two-dimensional coordinates , The image coordinates corresponding to the intersection of the imaging plane and the optical axis are recorded as (u0,v0) .
In the camera coordinate system , Points in space P And the corresponding image pixel coordinates (u,v) The relationship between is ：


The distortion of camera lens is not considered in the ideal small hole model , In fact, due to manufacturing and assembly reasons , Camera lens
Distortion in imaging . The commonly used distortion model is Brown Model , Radial distortion and tangential distortion are considered ,

Finally, a picture is used to summarize from the world coordinate system to the pixel coordinate system （ Distortion is not considered ） The transformation of ：

2. Homography matrix

Homography transformation （Homography） Transformation , Describe the position mapping relationship between the object in the world coordinate system and the pixel coordinate system , Homography matrix is defined as ：

among ,M It's the camera's internal parameter matrix

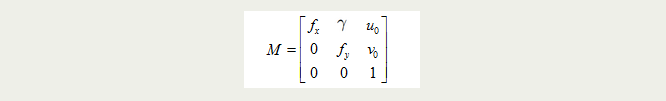
Homography is a very important concept in the field of computer vision , It is used in image correction 、 Image mosaic 、 Camera pose estimation 、 Vision SLAM And other fields play a very important role .

How to get the homography matrix according to the calibration diagram ？
1、 Print a checkerboard calibration drawing , Stick it on the surface of a flat object .
2、 Take a group of pictures of checkerboards in different directions , It can be achieved by moving the camera , You can also move the calibration picture to achieve .
3、 For each chessboard picture taken , Detect the feature points of all checkerboards in the picture （ Corner point , That is, the intersection of black and white chessboard in the figure below , Inside the magenta circle in the middle is a corner ）. We define that the printed chessboard drawing is located in the world coordinate system Zw=0 On the plane of , The origin of the world coordinate system is located at a fixed corner of the chessboard drawing （ For example, the yellow dot in the figure below ）. The origin of pixel coordinate system is located in the upper left corner of the picture .

4、 Because the spatial coordinates of all corners in the chessboard calibration drawing are known , The pixel coordinates of these corners corresponding to the corners in the captured calibration picture are also known , If we get this N>=4 Matching point pairs （ The more calculations, the more robust the results are ）, It can be based on LM The homography matrix is obtained by the optimization method H. Of course, the calculation of homography matrix generally does not need to write its own function ,OpenCV There are ready-made functions that can call , Corresponding c++ The function is :

Mat findHomography(InputArray srcPoints, InputArray dstPoints, int method=0, 
double ransacReprojThreshold=3, OutputArray mask=noArray() )

From the function definition , Just enter the matching point pair , Specify the specific calculation method to output the results .

The specific principle can be seen in （+ Reference resources ） Learn from scratch 「 Zhang's camera calibration method 」-- Computer vision life

3. Camera calibration

A typical ： Zhang Zhengyou - Checkerboard calibration method




notes : Manipulator hand eye calibration reference paper No 2 Chapter

Opencv Calibration process and API Introduce

opencv Binocular camera calibration - Sample code analysis ：https://blog.csdn.net/qq_15751687/article/details/117886678

4. Epipolar correction

Epipolar correction , Some are called stereo correction , The normal camera calibration process shall be the following process ：

1. Internal parameters obtained by camera calibration 、 External reference
2. Distortion correction
3. Stereo correction ( Epipolar correction )

See... For the specific principle ：
principle + Code combat | Epipolar correction in binocular vision ：https://blog.csdn.net/qq_42722197/article/details/118663803

opencv Realize the polar correction process ：
opencv Double target operation full version ：https://blog.csdn.net/hejingkui/article/details/80488763

The reference paper reproduces the stereo correction algorithm in order to realize three-dimensional reconstruction ：

The paper ：A Compact Algorithm for Rectification of Stereo Pairs
Reference resources ： A concise binocular correction algorithm –A Compact Algorithm for Rectification of Stereo Pairs

attach

4.1.matlab Realization

function [T1,T2,Pn1,Pn2] = rectify(Po1,Po2)
% RECTIFY: compute rectification matrices
% factorize old PPMs
[A1,R1,t1] = art(Po1);
[A2,R2,t2] = art(Po2);
% optical centers (unchanged)
c1 = - inv(Po1(:,1:3))*Po1(:,4);
c2 = - inv(Po2(:,1:3))*Po2(:,4);
% new x axis (= direction of the baseline)
v1 = (c1-c2);
% new y axes (orthogonal to new x and old z)
v2 = cross(R1(3,:)’,v1);
% new z axes (orthogonal to baseline and y)
v3 = cross(v1,v2);
% new extrinsic parameters
R = [v1’/norm(v1)
v2’/norm(v2)
v3’/norm(v3)];
% translation is left unchanged
% new intrinsic parameters (arbitrary)
A = (A1 + A2)./2;
A(1,2)=0; % no skew
% new projection matrices
Pn1 = A * [R -R*c1 ];
Pn2 = A * [R -R*c2 ];
% rectifying image transformation
T1 = Pn1(1:3,1:3)* inv(Po1(1:3,1:3));
T2 = Pn2(1:3,1:3)* inv(Po2(1:3,1:3));

% ------------------------
function [A,R,t] = art(P)
% ART: factorize a PPM as P=A*[R;t]

Q = inv(P(1:3, 1:3));
[U,B] = qr(Q);

R = inv(U);
t = B*P(1:3,4);
A = inv(B);
A = A ./A(3,3);

4.2.C++ Implementation reference

Principle and application of epipolar correction method C++ Realization ：https://www.freesion.com/article/7403499712/

C++ Realization qr decompose ： The projection matrix P Decompose into A( The essential matrix ),R( Rotation matrix ),T( Translation matrix )