当前位置:网站首页>Summary of floating point double precision, single precision and half precision knowledge
Summary of floating point double precision, single precision and half precision knowledge
2022-04-23 17:51:00 【ppipp1109】
Recently, I met a 16 The problem of half precision floating-point numbers , It's been a long time , Here we have studied , To sum up :
1. Single precision (32 position ) The structure of floating point numbers :

name length The bit Location
Sign bit Sign(S): 1bit (b31)
Index part Exponent(E): 8bit (b30-b23)
Mantissa part Mantissa(M): 23bit (b22-b0)
The exponential part (E) Offset code (biased) To express the positive and negative exponents , if E<127 Is a negative index , Otherwise, it is a nonnegative index .
Be careful :%f Output float type , Output 6 Decimal place , The number of significant digits is generally 7 position ;
2. Double precision (64 position ) The structure of floating point numbers

name length Bit position
Sign bit Sign (S) : 1bit (b63)
Index part Exponent (E) : 11bit (b62-b52)
Mantissa part Mantissa (M) : 52bit (b51-b0)
The exponential part of double precision (E) The offset code used is 1023
How to evaluate :(-1)S*(1.M)*2(E-1023) ( The formula 2)
Be careful : Double precision numbers are also available %f Format output , Its significant bit is generally 16 position , Give decimals 6 position .( This is particularly important when calculating the amount , Numbers that exceed the significant digits are meaningless , It usually makes mistakes .
3. Semi precision (16 position ) Floating point structure
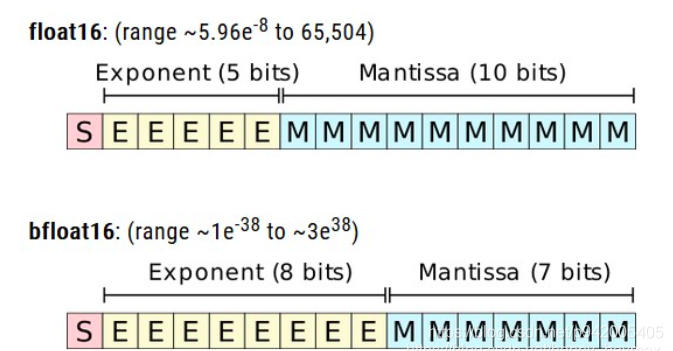
name length Bit position
Sign bit Sign (S) : 1bit (b15)
Index part Exponent (E) : 5bit (b14-b10)
Mantissa part Mantissa (M) : 10bit (b9-b0)
Recently, a kind of Bfloat16 How to count , Use the same number of digits as the half precision , It keeps the same exponential bit as the single precision, that is 8 Bits refer to digits , It can represent the same number range as single precision , But at the expense of decimal places, that is, precision .
Semi precision floating point is a kind of binary floating point data type used by computer . Semi precision floating point numbers use 2 byte (16 position ) Storage . stay IEEE 754-2008 in , It is called binary16. This type is only suitable for storing numbers that do not require high accuracy , Not suitable for calculating .
Half precision floating-point numbers are a relatively new type of floating-point numbers . NVIDIA in 2002 Released at the beginning of the year Cg Language defines it as half data type , And for the first time in 2002 Issued at the end of the year GeForce FX To realize .ILM We were looking for a way to have a high dynamic range , And do not need to consume too much hard disk and memory , And image formats that can be used for floating-point calculations like single precision floating-point numbers and double precision floating-point numbers . from SGI Of John Airey Led the hardware accelerated programmable coloring team in 1997 Invented as ’bali’ Part of the design work s10e5 data type . This was in SIGGRAPH2000 It was introduced in the paper in .( See Chapter 4.3) And patented in the United States 7518615 Further recorded in .
Semi precision floating-point numbers can include OpenEXR,JPEG XR,OpenGL,Cg Language and D3DX And several other computer graphics environments . And 8 Bit or 16 Comparison of bit integers , Its advantage is that it can improve the dynamic range , So that more details in high contrast pictures can be retained . Compared with single precision floating point numbers , Its advantage is that it only needs half of the storage space and bandwidth ( But at the expense of precision and numerical range )
Detailed explanation of semi precision floating point numbers :
IEEE754-2008 Contains a “ Semi precision ” Format , Only 16 A wide . So it is also called binary16, This type of floating-point number is only suitable for storing numbers that do not require high precision , Not suitable for calculation . Compared with single precision floating point numbers , Its advantage is that it only needs half of the storage space and bandwidth , But the disadvantage is the low accuracy .
The semi precision format is similar to the single precision format , The leftmost bit is still the sign bit , The index has 5 Wide and spare -16(excess-16) Form storage of , Mantissa has 10 A wide , But there is an implication 1.
As shown in the figure ,sign Symbol bit ,0 Indicates that the floating-point number is positive ,1 Indicates that the floating-point number is negative
Let's start with the mantissa , And the index ,fraction mantissa , Yes 10 Bit length , But there are implications 1, Mantissa can be understood as a floating point number, the number after the decimal point , Such as 1.11, The mantissa is 1100000000(1), The last implication 1 Mainly used in calculation , Implication 1 There may be situations where you can carry .
exponent Is the number of digits , Yes 5 Bit length , The specific values are as follows :
When the index is all 0 , The mantissa is also all 0 When the , That means 0
When the index is all 0, The trailing digits are not all 0 when , Expressed as subnormal value, Denormalized floating point numbers , It's a very small number
When the index is all 1, The mantissa is all 0 when , It means infinity , At this time, if the symbol bit is 0, Positive infinity , Symbol bit 1, Negative infinity
When the index is all 1, The trailing digits are not all 0 when , It's not a number
The rest of the time , Subtract... From the value of the exponential bit 15 Is the index it represents , Such as 11110 That means 30-15=15
So we can get , The calculation method of floating point number is half precision (-1)^sign×2^( The value of the exponential bit )×(1+0. mantissa )
remarks : here 0. mantissa , Indicates that the last digit is 0001110001, be 0. The last digits are 0.0001110001
Take a few examples :
The maximum value that can be expressed with half precision :0 11110 1111111111 The calculation method is as follows :(-1)^0×2^(30-15)×1.1111111111 = 1.1111111111×2^15, It's decimal 65504
The minimum value that can be represented by half precision ( except subnormal value):0 00001 0000000000 The calculation method is as follows :(-1)^(-1)×2(1-15)=2^(-14), Approximately equal to decimal 6.104×10^(-5)
Another ordinary number , The other way round this time , Such as -1.5625×10^(-1) , namely -0.15625 = -0.00101( Decimal to binary )= -1.01×2^(-3), So the sign bit is 1, Index is -3+15=12, So the exponent is 01100, The last digits are 0100000000. therefore -1.5625×10^(-1) Expressed as a semi precision floating-point number, it is 1 01100 0100000000
Code measurement :
Float16ToFloat32:
You can put 16 Bit float IEEE754 canonical int Value to 32 Bit float
float Float16ToFloat( short fltInt16 )
{
int fltInt32 = ((fltInt16 & 0x8000) << 16);
fltInt32 |= ((fltInt16 & 0x7fff) << 13) + 0x38000000;
float fRet;
memcpy( &fRet, &fltInt32, sizeof( float ) );
return fRet;
}Float32ToFloat16:
You can put 32 Of float IEEE754 The specification is transformed into 16 position int value
short FloatToFloat16( float value )
{
short fltInt16;
int fltInt32;
memcpy( &fltInt32, &value, sizeof( float ) );
fltInt16 = ((fltInt32 & 0x7fffffff) >> 13) - (0x38000000 >> 13);
fltInt16 |= ((fltInt32 & 0x80000000) >> 16);
return fltInt16;
}Reference link :
版权声明
本文为[ppipp1109]所创,转载请带上原文链接,感谢
https://yzsam.com/2022/04/202204230549076149.html
边栏推荐
- 2022制冷与空调设备运行操作判断题及答案
- Chrome浏览器的跨域设置----包含新老版本两种设置
- Kubernetes 服务发现 监控Endpoints
- STM32 entry development board choose wildfire or punctual atom?
- 2022 Shanghai safety officer C certificate operation certificate examination question bank and simulation examination
- HCIP第五次实验
- Welcome to the markdown editor
- Qt 修改UI没有生效
- PC电脑使用无线网卡连接上手机热点,为什么不能上网
- Future usage details
猜你喜欢
Index: teach you index from zero basis to proficient use
Learning record of uni app dark horse yougou project (Part 2)
Kubernetes 服务发现 监控Endpoints
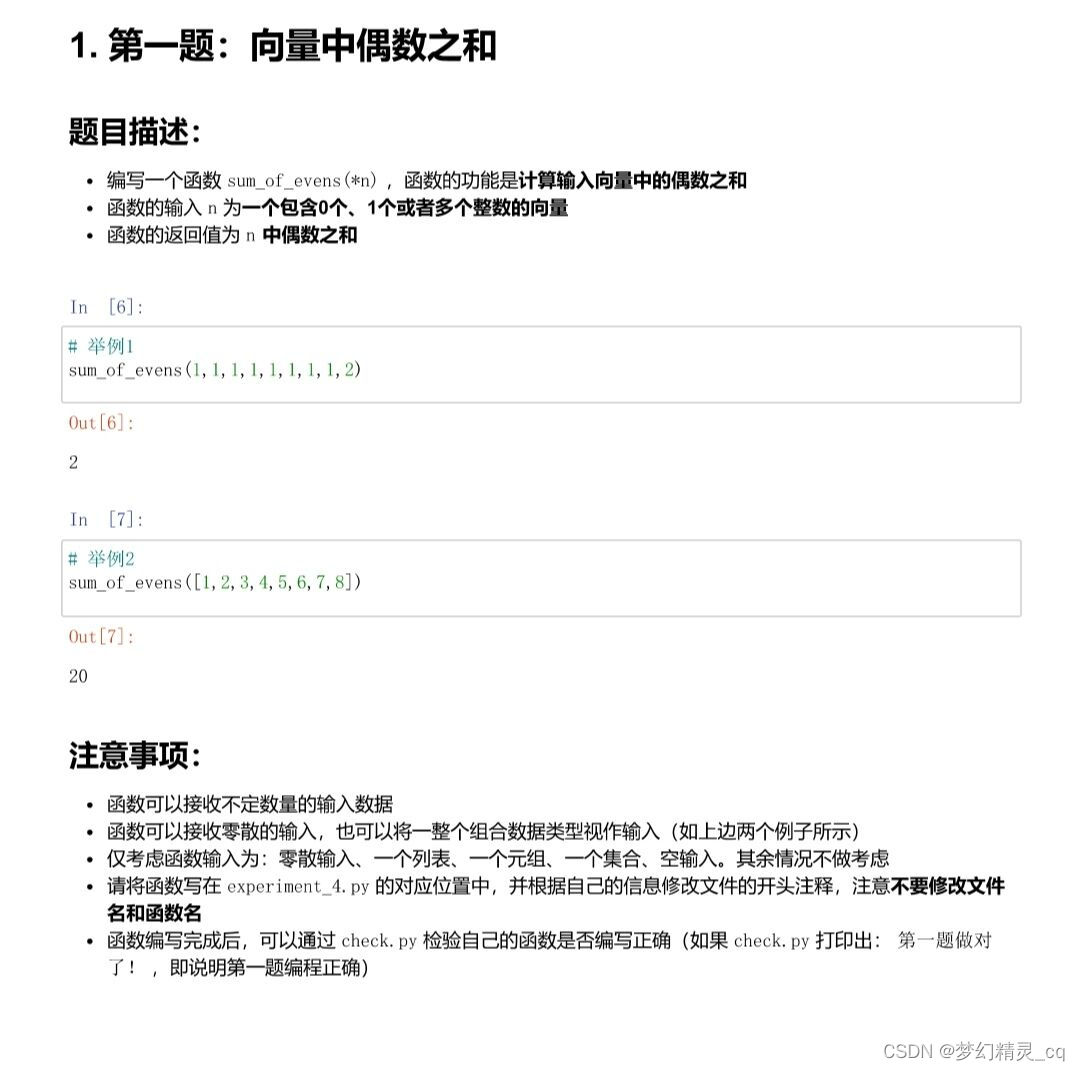
Exercise: even sum, threshold segmentation and difference (two basic questions of list object)

2022年上海市安全员C证操作证考试题库及模拟考试
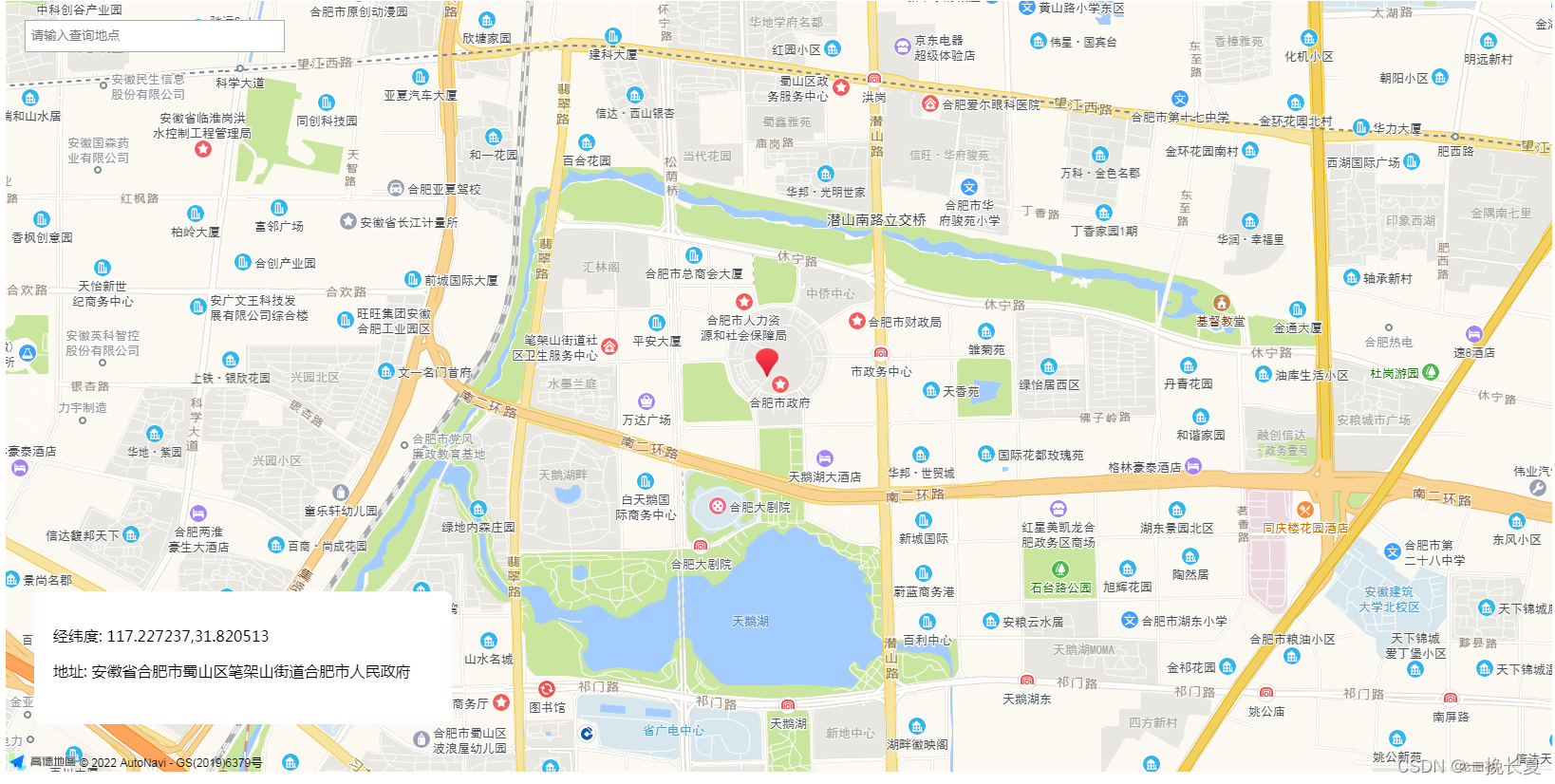
高德地图搜索、拖拽 查询地址
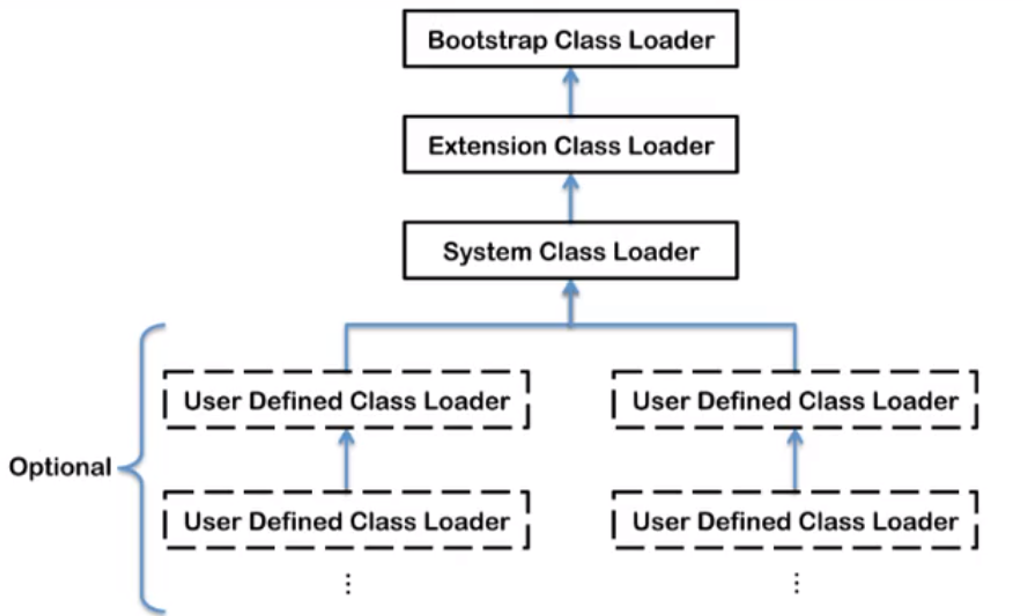
JVM类加载机制
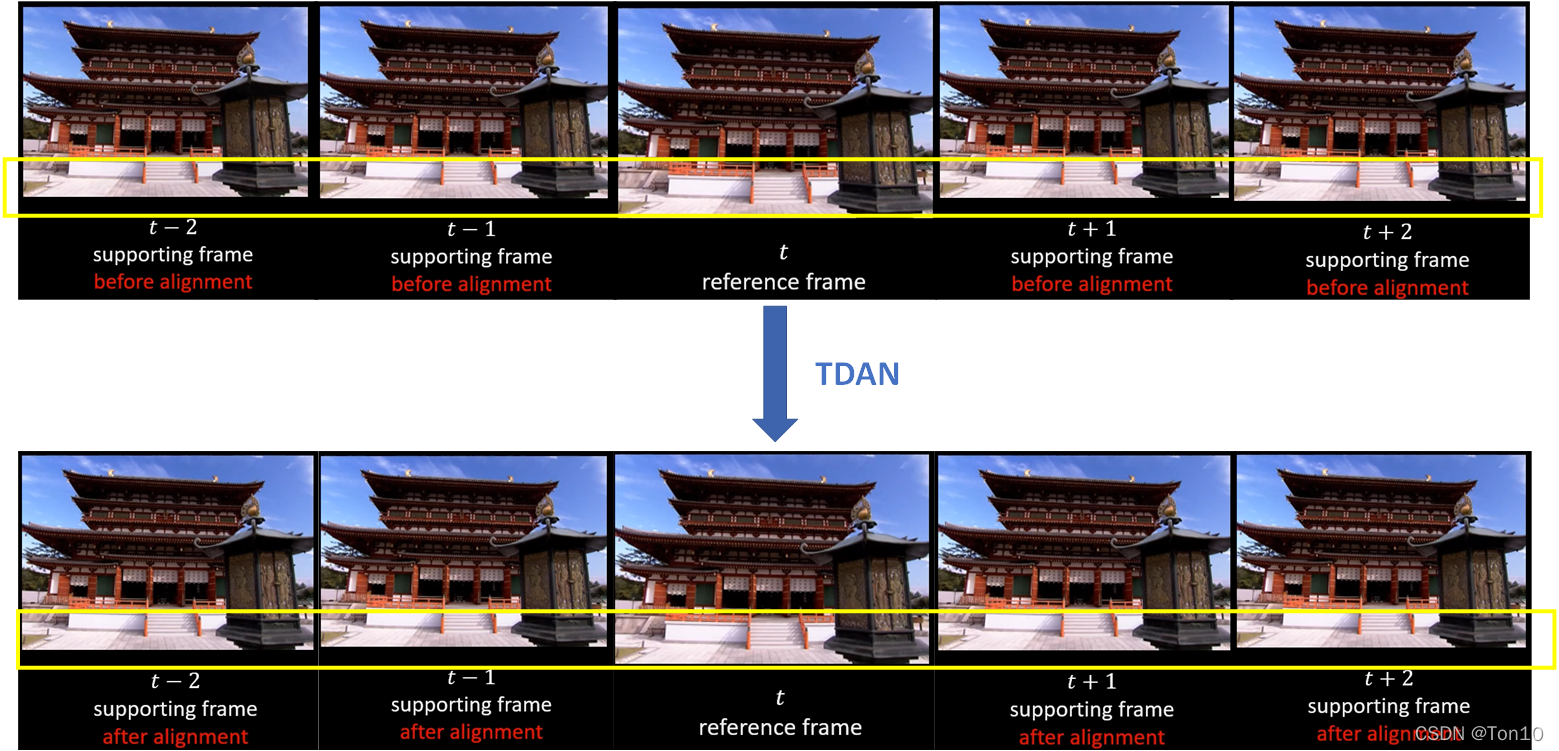
超分之TDAN

440. 字典序的第K小数字(困难)-字典树-数节点-字节跳动高频题
In embedded system, must the program code in flash be moved to ram to run?
随机推荐
Kubernetes service discovery monitoring endpoints
Anchor location - how to set the distance between the anchor and the top of the page. The anchor is located and offset from the top
读《Software Engineering at Google》(15)
Qt error: /usr/bin/ld: cannot find -lGL: No such file or directory
Read software engineering at Google (15)
開期貨,開戶雲安全還是相信期貨公司的軟件?
PC电脑使用无线网卡连接上手机热点,为什么不能上网
node中,如何手动实现触发垃圾回收机制
C1小笔记【任务训练篇二】
Construction of functions in C language programming
470. 用 Rand7() 实现 Rand10()
Entity Framework core captures database changes
41. The first missing positive number
[binary number] maximum depth of binary tree + maximum depth of n-ary tree
Listen for click events other than an element
JVM class loading mechanism
Open source key component multi_ Button use, including test engineering
In ancient Egypt and Greece, what base system was used in mathematics
2022 Shanghai safety officer C certificate operation certificate examination question bank and simulation examination
Utilisation de la liste - Ajouter, supprimer et modifier la requête