当前位置:网站首页>【Study Notes】Unused graph theory knowledge
【Study Notes】Unused graph theory knowledge
2022-08-11 10:53:00 【OneInDark】
斯坦纳树
不看 c 9 \sf c9 c9 I didn't even know there was such a thing.It is true that the food has reached a certain level.
目标是,In an undirected graph with nonnegative edge weights,Select the connected subgraph with the minimum edge weight and minimum,使得 k k k a given point in the graph.Obviously only trees will be selected,Trees have roots.于是可以 d p \tt dp dp,记 f ( x , S ) f(x,S) f(x,S) 为 x x x Connect the rooted tree S S S The minimum cost of keypoints within .
The root has only one son f ( x , S ) ← f ( y , S ) + w ( x , y ) f(x,S)\gets f(y,S)+w(x,y) f(x,S)←f(y,S)+w(x,y),There are multiple sons f ( x , S ) ← f ( x , T ) + f ( x , S ∖ T ) ( T ≠ ∅ , T ⫋ S ) f(x,S)\gets f(x,T)+f(x,\;S\setminus T)\;(T\ne\varnothing,\;T\subsetneqq S) f(x,S)←f(x,T)+f(x,S∖T)(T=∅,T⫋S) .
转移顺序,Obviously follow ∣ S ∣ |S| ∣S∣ 升序.或者按照 S S S 升序,in the binary value sense.Then it is easy to do the second type of transfer,Subset enumeration.
The first type of transition is the shortest-path transition,可以直接 dijkstra \texttt{dijkstra} dijkstra 等.
Card often:应让 S S S is the first dimension of the array,In this way, the memory access in the shortest time is very continuous.同时,The second type of transfer should also be enumerated first T T T 再枚举 i i i .
最小直径生成树
Enumerates the midpoint of the diameter,Then the answer is its furthest distance to all points multiplied by it 2 2 2 .If that's not the midpoint,The value is too large.
So just find the midpoint of the graph,i.e. minimize its furthest distance to all points.
Find the shortest path to all sources,Then find the best point on each edge.是个 O ( n ) \mathcal O(n) O(n) Piecewise function,每段的 min \min min 易求.复杂度 O ( n m ) \mathcal O(nm) O(nm) .
最小树形图
目标是,on a weighted directed graph,Find the subgraph that satisfies the edge weights and the smallest sum r r r There is a unique path to each point(That is, a tree diagram).It doesn't matter whether the frontier rights are non-negative or not,Because adding big positive numbers to all sides is enough.
Because it is more like a minimum spanning tree,所以可以贪心.有点不自然?But the logic is relatively strict.This is called the Zhu Liu algorithm.
The dendrogram is equivalent to giving except r r r Each point of , selects the incoming edge,Make the graph acyclic.因此,给 r r r Points other than the least weighted edge are selected,If this can form a treemap,That must be the best solution.
否则(There is an optimal solution such that )There must be exactly one edge on the ring not selected.Because one side is not selected,Description cannot be adjusted,Shows that the points on both sides have the opposite reachability relation to this edge;Uncheck if there are at least two edges on the ring,A circular reachability relationship can be derived,矛盾.
So the ring can be reduced to a single point,The outside-to-inward edge becomes to replace the original incoming edge,That is, the edge weight of the original incoming edge is subtracted.This new single point also selects only one incoming edge,i.e. replace an edge,符合预期.
At least one point can be reduced per round(Not all points are in the ring,There may be only two points in the loop,The rest of the points form a dendrogram),总复杂度 O ( n m ) \mathcal O(nm) O(nm),The actual operation should run unsatisfactory.
还有个 tarjan \textsf{tarjan} tarjan 算法.Make all points oriented r r r 的连边,边权为 + ∞ +\infty +∞,It is not difficult to verify that this process is correct:维护一个栈,Initially there are arbitrary points in it a a a,Remove the top of the stack and its smallest incoming edge each time,Select the incoming edge.If the selected incoming edges form a ring,Apparently some points at the top of the stack,缩点(The new point remains on top of the stack),Continue this process until only one point remains in the entire graph.
Use union search to deal with shrink points,Use can be stacked(带标记)It is enough to maintain the entry edge of each point.复杂度 O ( m log m ) \mathcal O(m\log m) O(mlogm) .
Comment. 奶奶滴,Why I figured out the complexity and OI-wiki \text{OI-wiki} OI-wiki It's written differently
边栏推荐
- How to analyze the neural network diagram, draw the neural network structure diagram
- B端产品需求分析与优先级判断
- form-making爬坑笔记(jeecg项目替换表单设计器)
- 09什么是继承
- 阿里内网疯传的P8“顶级”分布式架构手册被我拿到了
- NT 内核函数原型大全
- 放苹果
- What is the difference between the qspi interface and the ordinary four-wire SPI interface?
- servlet——servlet介绍 | 发布动态资源
- 1.TCP/IP基础知识
猜你喜欢

Qihua stores the future and interprets the origin of distributed
The crawler is encapsulated into an api
LeetCode 剑指 Offer 35. 复杂链表的复制
阿里云ssl证书申请,宝塔ssl证书部署
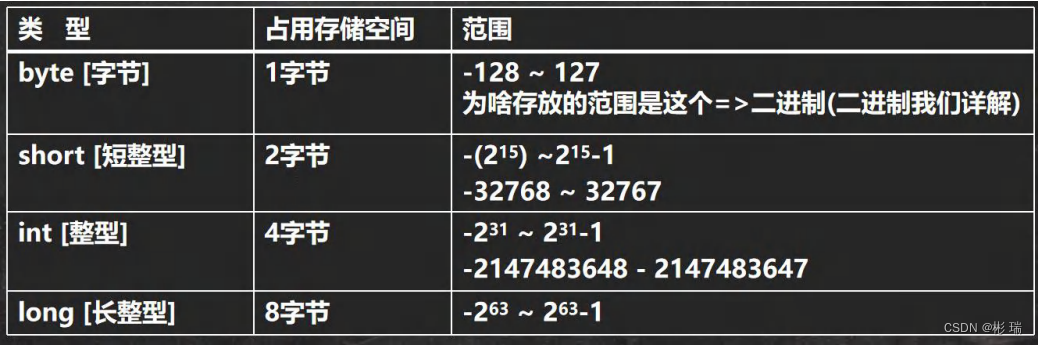
二、第二章变量
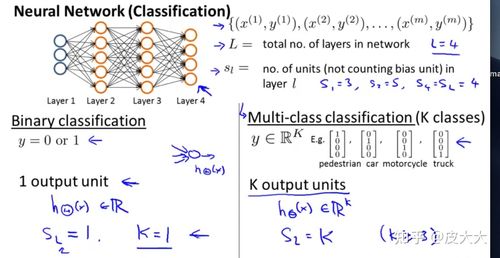
How to determine the neural network parameters, the number of neural network parameters calculation
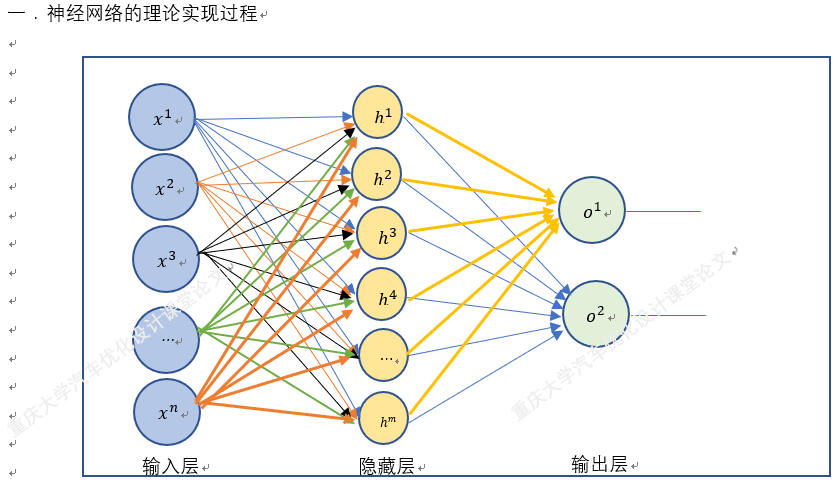
How to analyze the neural network diagram, draw the neural network structure diagram
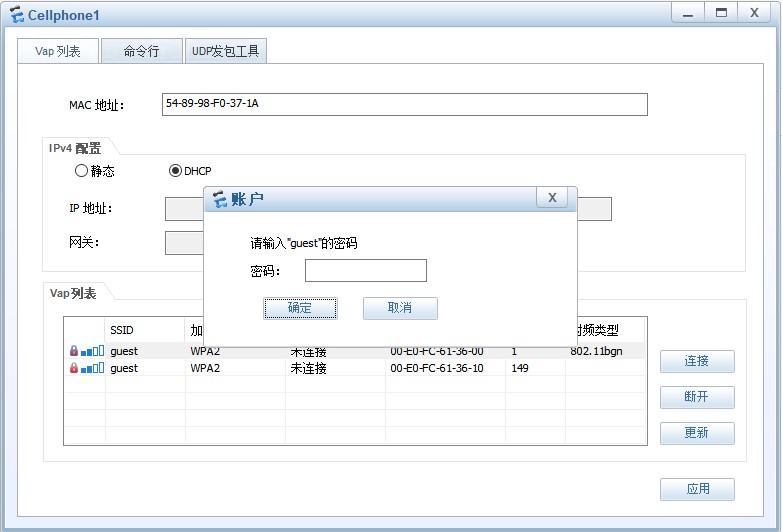
Huawei WLAN Technology: AC/AP Experiment

你觉得程序员是一个需要天赋的职业吗?
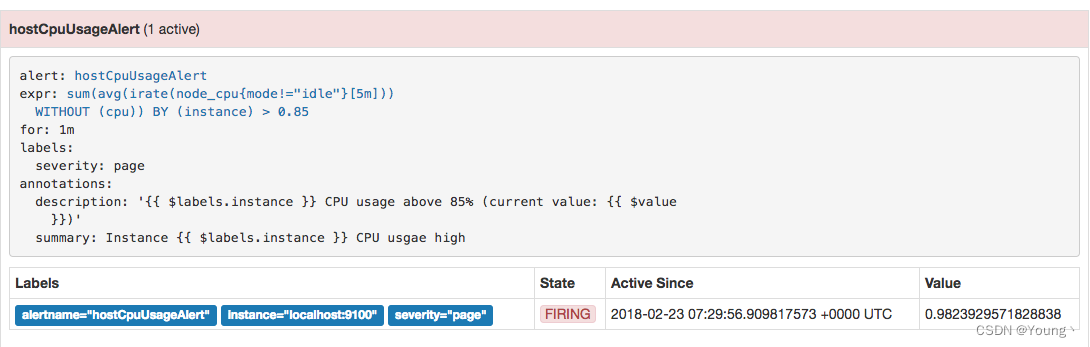
【Prometheus】Alertmanager告警全方位讲解
随机推荐
如何解决 “主节点故障恢复的自动化” 问题?
爬虫封装成api
中小企业如何实施MES管理系统
【无标题】(完美解决)uni-app 小程序下拉刷新后刷新图标无法正常恢复的问题
php获取微信小程序码并存储到oss
chrome插件开发入门-保姆级攻略
漫画手绘之临摹篇
Deploying Robot Vision Models Using Raspberry Pi and OAK Camera
数据库的索引和其底层数据结构
二维数组名的用途
SAP Product Enhancement Technology Review
全新FIDE 编译简单评测
> 家乡旅游景点网页作业制作 网页代码运用了DIV盒子的使用方法,如盒子的嵌套、浮动、margin、border、backgro
form-making爬坑笔记(jeecg项目替换表单设计器)
Six functions of enterprise exhibition hall production
MySQL表sql语句增删查改_修改_删除
a sequence of consecutive positive numbers with sum s
【Prometheus】 Grafana数据与可视化
大疆2022秋招笔试 —— 最小时间差、数组的最小偏移量
OAK-FFC Series Product Getting Started Guide