当前位置:网站首页>赛氪-zeal
赛氪-zeal
2022-04-23 05:51:00 【Round moon】
zeal
题目描述
Yassin 最近在量化投资方面很有兴趣。
为了研究哪只股票是真正的牛股,他把历史 nn 天每一天成交量最大的股票代码写成了一排,并构建了一套属于自己的“理论体系”。
成交量多说明人气好,人气好的肯定买的人多,赚钱就要靠人气! – Yassin
但是知道的人太多,这个大家都去接盘,那就都成为韭菜了 – Makik
基于这个理论,Yassin 想知道 [L, R] 区间中人气“比较”好的股票有哪些,具体而言,他会给定你 L, R, k,你则需要告诉他 [L, R] 中出现 k 次的股票有多少只。
例如 n = 5 时,假设这个代码序列为 {1, 1, 2, 3, 1} 现在他给了一个询问 (2, 5, 1),你就需要回答他 {a2,a3,a4,a5} 中恰好出现 1 次的有多少种元素。答案显然为 2,恰好出现一次的元素为 2,3。
数据保证 0<ai,k<=n<=4×104,q<=104,L<=R。
输入
第一行 2 个数字 n, q, 分别表示序列的长度和询问的个数。
接下来一行 nn 个数字,为序列 an
接下来 qq 行,每行三个数字 L, R, k, 如题目描述所述。
输出
共 q 行,每行一个数字,为对应询问的答案。
Sample Input
5 1
1 1 2 3 1
2 5 1
Sample Output
2
思路解析
这是一个基础的莫队模板题,如果没有头绪,可以看下面的GIF图你就能明确了。
以
10 10
5 9 4 9 10 6 1 4 6 8
3 7 1
6 8 1
1 8 1
5 10 1
1 5 1
3 7 1
2 5 1
8 10 1
1 10 1
9 10 1
因为我们是从0开始计算的,所以我们每个位置都要减一。
这个数据为例,我们来探究。
莫队第一步,分块。至于为什么分块,请看其余的博客,了解莫队算法,这里我们默认知道第一步就是要分块,做离线处理。
首先先对数据进行分块。

接下来对我们的数据进行排序,做分块离线处理。
//排序方法
bool cmp(node a, node b)
{
if (block[a.l] == block[b.l])
{
if (block[a.l] & 1) return a.r < b.r;
return a.r > b.r;
}
return block[a.l] < block[b.l];
}
我们直接看最后的结果
| 序号 | L | R |
|---|---|---|
| 1 | 0 | 4 |
| 2 | 1 | 4 |
| 3 | 2 | 6 |
| 4 | 2 | 6 |
| 5 | 0 | 7 |
| 6 | 0 | 9 |
| 7 | 4 | 9 |
| 8 | 5 | 7 |
| 9 | 7 | 9 |
| 10 | 8 | 9 |
我们可以发现1-6为第0块,我们的排序方法是按照R的值升序排序,7-8是第一块我们降序排序,9-10为第三块,升序排序。排序过程就不过多赘述,下面我们就开始我们核心算法。两个指针的移动。

莫队的核心思想有点像dp,比如
你要算100的阶乘,如果告诉你99的阶乘那么你直接乘以100就可以,如果告诉你99的阶乘,要算98的阶乘,那么除99就可以了。
我们这里就有一个答案区间,每当指针移动的时候我们就更新这个区间,去掉的元素删除,新增的元素添加。
这里妙就妙在分块,成功的优化了暴力的复杂度,也就是说我们把这个数据变得理想化,让我们去执行起来很方便。
这里说一下,排序的时候让每一块的升降序规则不一样,这样能够保证我们可以走到最远处之后还可以沿着原路走回最近处,再沿着最近处走到最远处。
Accepted Code
//#include<unordered_map>
#include<algorithm>
#include<iostream>
#include<string.h>
#include <iomanip>
#include<stdio.h>
#include<vector>
#include<string>
#include<math.h>
#include<cmath>
#include<queue>
#include<stack>
#include<deque>
#include<map>
#include<set>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const ll ll_inf = 9223372036854775807;
const int int_inf = 2147483647;
const short short_inf = 32767;
const ll less_inf = 0x3f3f3f3f;
const char char_inf = 127;
#pragma GCC optimize(2)
#define accelerate cin.tie(NULL);cout.tie(NULL);ios::sync_with_stdio(false);
#define PI 3.141592653589793
#define EPS 1.0e-8
ll gcd(ll a, ll b) {
return b ? gcd(b, a % b) : a;
}
ll lcm(ll a, ll b) {
return a / gcd(a, b) * b;
}
inline ll read() {
ll c = getchar(), Nig = 1, x = 0;
while (!isdigit(c) && c != '-')c = getchar();
if (c == '-')Nig = -1, c = getchar();
while (isdigit(c))x = ((x << 1) + (x << 3)) + (c ^ '0'), c = getchar();
return Nig * x;
}
inline void out(ll a) {
if (a < 0)putchar('-'), a = -a;
if (a > 9)out(a / 10);
putchar(a % 10 + '0');
}
ll qpow(ll x, ll n, ll mod) {
ll res = 1;
while (n > 0) {
if (n & 1)res = (res * x) % mod;
x = (x * x) % mod;
n >>= 1;
}
return res;
}
#define read read()
const int N = 4 * 1e4;
int block[N + 7];
struct node
{
int l, r, ask, id, ans;
}query[N + 7];
int save[N + 7];
bool cmp(node a, node b)
{
if (block[a.l] == block[b.l])
{
if (block[a.l] & 1) return a.r > b.r;
return a.r < b.r;
}
return block[a.l] < block[b.l];
}
int res[N + 7];
int cnt[N + 7];
void del(int num)
{
res[cnt[num]]--;
cnt[num]--;
res[cnt[num]]++;
}
void add(int num)
{
res[cnt[num]]--;
cnt[num]++;
res[cnt[num]]++;
}
int main()
{
int n = read, m = read;
int base = sqrt(n);
for (int i = 0; i < n; i++)
block[i] = i / base;
for (int i = 0; i < n; i++)save[i] = read;
for (int i = 0; i < m; i++)
{
query[i].l = read - 1, query[i].r = read - 1, query[i].ask = read;
query[i].id = i;
}
sort(query, query + m, cmp);
int l = 0, r = 0;
cnt[save[0]]++;
res[1]++;
for (int i = 0; i < m; i++)
{
int nowl = query[i].l, nowr = query[i].r;
while (l < nowl)del(save[l++]);
while (l > nowl)add(save[--l]);
while (r < nowr)add(save[++r]);
while (r > nowr)del(save[r--]);
query[i].ans = res[query[i].ask];
}
sort(query, query + m, [](node a, node b) {
return a.id < b.id; });
for (int i = 0; i < m; i++)
cout << query[i].ans << endl;
return 0;
}
By-Round Moon
版权声明
本文为[Round moon]所创,转载请带上原文链接,感谢
https://blog.csdn.net/qq_35339563/article/details/120901666
边栏推荐
- Swagger2 generates API documents
- 深蓝学院激光slam 理论与实践 第三章激光雷达去畸变 作业习题
- [stepping on the pit] MELD in win11 wsl2 cannot be used normally. Problem repair
- sqlite3加密版
- [UDS unified diagnosis service] IV. typical diagnosis service (1) - diagnosis and communication management function unit
- [opencv] use filestorage to read and write eigenvectors
- SSH 公钥 私钥的理解
- 共用数据的保护
- 【UDS统一诊断服务】二、网络层协议(2)— 数据传输规则(单帧与多帧)
- C语言实现memcpy、memset、strcpy、strncpy、strcmp、strncmp、strlen
猜你喜欢
基于VGG对五种类别图片的迁移学习
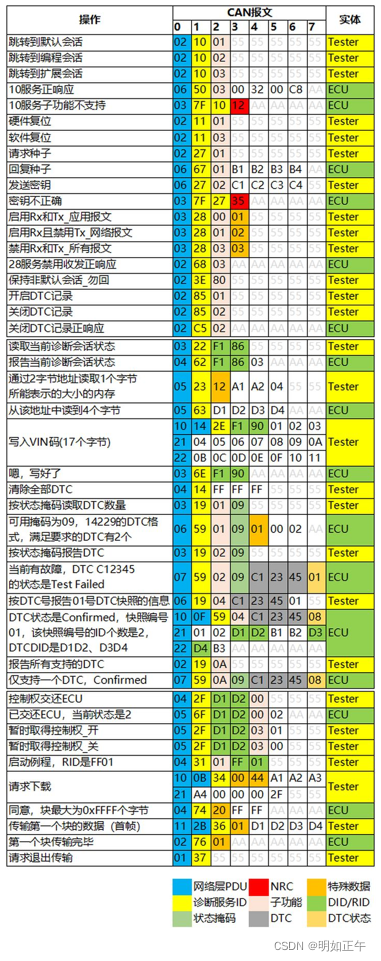
【UDS统一诊断服务】四、诊断典型服务(1)— 诊断和通信管理功能单元

gcc ,g++,gdb的安装
![[UDS unified diagnosis service] IV. typical diagnosis service (3) - read fault information function unit (storage data transmission function unit)](/img/10/bd39bb03f5456a412650596208a391.png)
[UDS unified diagnosis service] IV. typical diagnosis service (3) - read fault information function unit (storage data transmission function unit)

FOC 单电阻采样 位置环控制伺服电机
QT add qserialport class to realize serial port operation

Shell脚本 &&和||的使用

基于VGG卷积神经网络的图像识别代码实现
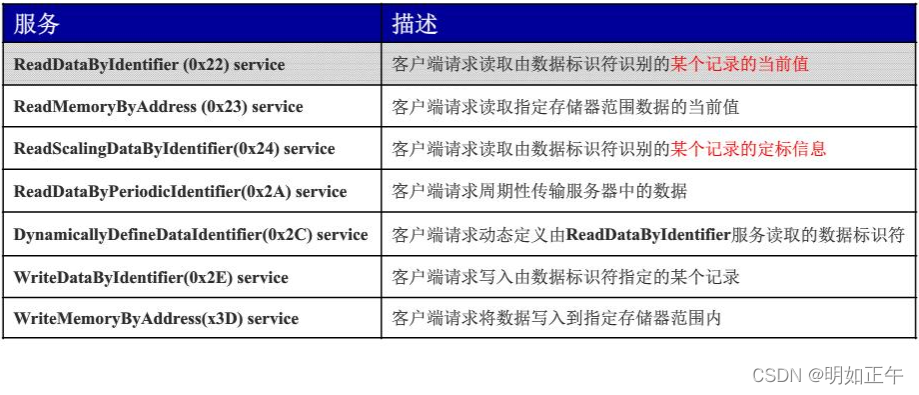
【UDS统一诊断服务】四、诊断典型服务(2)— 数据传输功能单元
Vscode custom comments
随机推荐
Protection of shared data
Friend function, friend class, class template
C#【文件操作篇】按行读取txt文本
【UDS统一诊断服务】三、应用层协议(2)
vs中的多字节与unicode
猜數字遊戲
[stepping on the pit] MELD in win11 wsl2 cannot be used normally. Problem repair
Generate random number
Uniapp encapsulates request
OpenCV使用 GenericIndex 进行 KNN 搜索
函数的调用过程
文件查看命令和用户管理命令
[untitled]
Quaternion multiplication
Collection of practical tips for C language (continuously updated)
C语言实现memcpy、memset、strcpy、strncpy、strcmp、strncmp、strlen
POJ-The Unique MST
C51/C52 特殊功能寄存器表
Swagger2 generates API documents
[UDS unified diagnostic service] II. Network layer protocol (1) - overview and functions of network layer