当前位置:网站首页>2022.8.9 Mock Competition
2022.8.9 Mock Competition
2022-08-10 21:26:00 【aWty_】
T0
小清新签到题,直接暴力 b f s bfs bfs 就过掉了,But have you ever been walked to record each letter in the middle,Don't go through.Or if the picture is all the same letter time complexity just blew up Here is the hang up 9 分.
T1 Jacob arithmetic of
Allows you to quickly determine the score p q \frac pq qp 在 b b b Whether in base for infinite decimals.
According to some common sense,我们知道 p q \frac pq qp Whether the cycle with p p p 没啥关系,So let's give them a reduction of a fraction and then focus on q q q(Here are special for p = 0 p = 0 p=0).
Then we found that give a number 1 q \frac 1q q1 乘上一个 b b b 就相当于在 b b b Base the decimal point moves to the right a.So if the decimal is limited,那么就存在一个 k ∈ N ∗ k \in N^* k∈N∗ 使得 q ∣ b k q \mid b^k q∣bk.
So we will consider has been to q q q 除上 gcd ( q , b ) \gcd(q, b) gcd(q,b),Until the two thing co-prime.此时如果 q = 1 q = 1 q=1 那么就说明 q q q 的质因子 b b b 都有.So that is there k k k 使得 q ∣ b k q \mid b^k q∣bk,时间复杂度是 O ( T log 2 q ) O(T\log^2q) O(Tlog2q) 的.
T2 Jacob paint the walls
20pts
有 20 p t s 20pts 20pts Is a rectangular case,According to the computer room bosses c m y cmy cmy The law of the said this part is better looking for,答案就是:
a n s = 2 n + 2 h − 2 ans = 2^n + 2^h - 2 ans=2n+2h−2
就直接 O ( log n ) O(\log n) O(logn) Finished it quickly power.
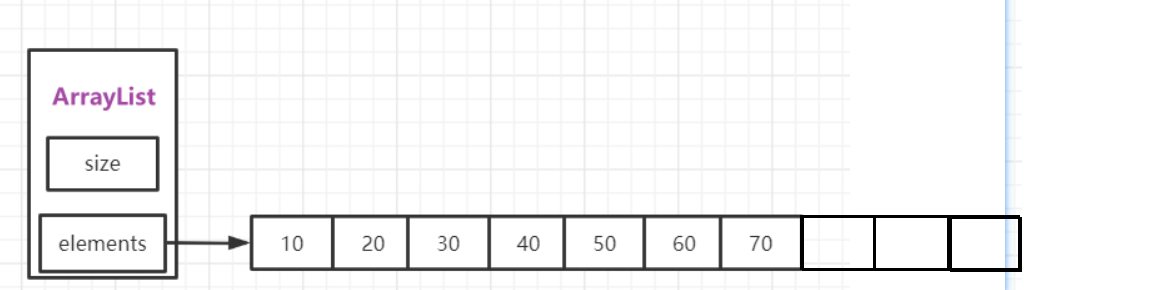
T3 Jacob data structure
10pts
Simulated according to the problem face directly,复杂度 O ( m n 2 ) O(mn^2) O(mn2).
40 pts
Maintaining a line segment tree support single point change,区间查询,我们发现一个性质,对于一个左端点 i i i 来说,After her extension to the right of o r or or Value is strictly monotone increasing,So we can consider to get a binary point p o s pos pos,This is the first greater than or equal to x x x 的右端点,那么这个点 i i i 的贡献就是 v − p o s + 1 v - pos + 1 v−pos+1.
Binary every time c h e c k ( m i d ) check(mid) check(mid) To segment tree range check,所以复杂度是 O ( m n log n ) O(mn\log n) O(mnlogn) 的.
50 pts
因为 x = 0 x = 0 x=0,所以答案就是:
a n s = 1 2 ( r − l + 1 ) ( r − l + 2 ) ans = \frac 12(r - l + 1)(r - l + 2) ans=21(r−l+1)(r−l+2)
70pts
边栏推荐
猜你喜欢
随机推荐
2021DASCTF实战精英夏令营暨DASCTF July X CBCTF 4th
ArcPy读取Excel时序数据、批量反距离加权IDW插值与掩膜
Uniapp编译后小程序的代码反编译一些思路
基于Pix4Dmapper的运动结构恢复法无人机影像三维模型重建
ES6中的for...in/of的使用
mysql服务器参数设置
【golang map】 深入了解map内部存储协议
PostgreSQL — 安装及常用命令
2021 GKCTF X DASCTF应急挑战杯
CGO 初步认知和基本数据类型转换
Redis命令手册
DDL:ALTER 修改数据库——《mysql 从入门到内卷再到入土》
组合导航精度分析
Kubernetes 笔记 / 入门 / 生产环境 / 用部署工具安装 Kubernetes / 用 kubeadm 启动集群 / 用 kubeadm 创建集群
Web3中值得关注的基础设施
玩转doxygen 之RT-THREAD
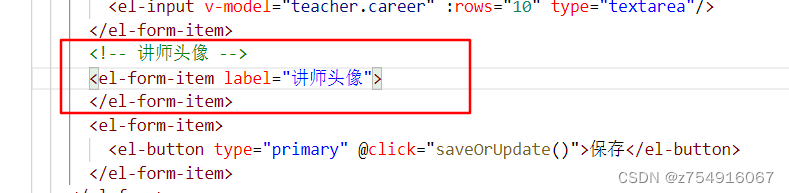
直播课堂系统09--腾讯云点播管理模块(一)
npm warn config global `--global`, `--local` are deprecated. use `--location=global` instead.
paddle 35 paddledetection保存训练过程中的log信息
kuberentes Auditing 入门