当前位置:网站首页>Code Casual Recording Notes_Dynamic Programming_70 Climbing Stairs
Code Casual Recording Notes_Dynamic Programming_70 Climbing Stairs
2022-08-10 13:07:00 【Erik_Won】
代码随想录二刷笔记记录
LC70.爬楼梯
题目
完全背包
假设你正在爬楼梯.需要 n 阶你才能到达楼顶.
每次你可以爬 1 或 2 个台阶.你有多少种不同的方法可以爬到楼顶呢?
示例 1:
输入:n = 2
输出:2
解释:有两种方法可以爬到楼顶.
- 1 阶 + 1 阶
- 2 阶
示例2:
输入:n = 3
输出:3
解释:有三种方法可以爬到楼顶.
- 1 阶 + 1 阶 + 1 阶
- 1 阶 + 2 阶
- 2 阶 + 1 阶
提示:
1 <= n <= 45
思路分析1
方法1:归纳
动态规划五部曲
1.确定dpArray and subscript meaning
dp[i] 的定义: 第 i The number represents the climb to the first i 层有 dp[i] 个方案
2.确定递推公式
要爬 n 阶楼梯,
Suppose we are in the first n-1 层台阶时,有dp[n-1]个方案,再爬1One steps to the top.
在第 n-2 步时,有dp[n-2]个方案,再爬 2 One steps to the top.
Assuming to climb n The function of the stairs is f ,则有
f(n) = f(n-1) + f(n-2)
dp[i] = dp[i-1] + dp[i-2]
3.dp数组初始化
依题意,最少要2个台阶,因此第0Layers have no methods -> dp[0] = 0 (这里无论dp[0] = 多少,都是没有意义的,Because of traversal fromdp[2]开始,所以 dp[0] whatever equals1 还是 0 都无所谓)
第1层有 1 种方法,Just a step dp[1] = 1,
第2层有 2 种方法,1+1 和 2 ,因此 dp[2] = 2
4.确定遍历顺序
由递推公式 dp[i] = dp[i-1] + dp[i-2] 可知, 第 i The scheme of the layer ladder depends on the first i-1 层有dp[i-1]Programs and Articles i-2 层有 dp[i-2] 个方案,Therefore, it is traversed from front to back.
5.推演分析
以 n = 6 为例
dp[3] = 3, dp[4] = 5 ,dp[5] = 8,dp[6] = 13
代码实现1
完整代码实现
public int climbStairs(int n) {
//特判
if (n <= 2) return n;
//初始化
int[] dp = new int[2];
dp[1] = 1;
dp[2] = 2;
int method = 0;
//遍历
for (int i = 3;i <= n;i++){
method = dp[i-1] + dp[i-2];
dp[i-2] = dp[i-1];
dp[i-1] = method;
}
return method;
}
思路分析2
方法2:动态规划_完全背包
Solve in a completely knapsack approach 70 题
由题,分析可知: 物品为 One step,Second step.背包容量:Climb to the top floors
Steps can be taken repeatedly,So this problem is a complete knapsack problem.
动态规划五部曲
1.确定dp数组及其下标含义
dp[j]: 爬到 j 层的楼,有 dp[j] 种方法
2.递推公式
由 LC494,377,518 可知,Review the recursive formula for several ways to fill a backpack
dp[j] += dp[j - nums[i]]
而本题,求第 j 层台阶的方法dp[j] , 由之前的dp[j-1],dp[j-2],… 推导而来
因此,递推公式为
dp[j] += dp[j-i]
3.初始化
dp[0] = 1,and the previous topicLC494,377,518一样,The first item needs to be initialized as 1,Otherwise, subsequent derivations will be affected.
4.遍历顺序
由示例2可知,1阶 + 2阶 和 2阶 + 1阶 不同,因此可以确定,The answers to this question are various排列的总数.求排列,The traversal order we use is 先遍历背包,后遍历物品.
for(i = 0;i <= n;i++){
//背包
for(j = 1;j <= 2;j++){
//物品
if(i >= j){
//当背包容量 >= 物品时,Calculations make sense
dp[i] += dp[i - j];
}
}
}
5.推演分析
以 n = 3 为例
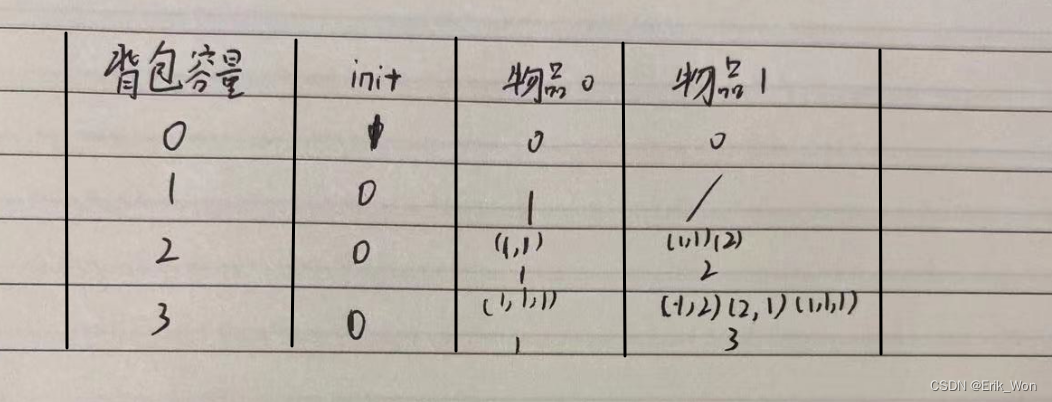
代码实现2
public int climbStairs(int n) {
if (n <= 2) return n;
//初始化
int[] dp = new int[n + 1];
dp[0] = 1;
//先遍历背包,后遍历物品
for (int i = 0; i <= n; i++) {
//背包
for (int j = 1; j <= 2; j++) {
//物品
//背包容量 > 物品时,才开始更新
if (i >= j){
dp[i] += dp[i - j];
}
}
}
return dp[n];
}
总结
Complete backpack usage for this question,进行一个回顾
1.递推公式
For combinatorial problems,The formula we generally use is
dp[i] += dp[j - nums[i]]
2.遍历顺序
Combination problems We also need to consider the problem of traversal order,Examples based on the title,我们可以判断,如:(1,2) 和 (2,1) Is it the same answer.是,It means that the question considers a combination problem;否,It means that what we are looking for is a permutation problem.
- 组合问题:先遍历物品,后遍历背包
- 排列问题:先遍历背包,后遍历物品
小拓展
一步一个台阶,两个台阶,三个台阶,直到 m个台阶,How many ways to get there n 阶楼顶.
代码实现
public int climbStairs(int n) {
int[] dp = new int[n+1];
dp[0] = 1;
for (int i = 1;i <= n;i++){
for(int j = 1; j<= m; j++){
//m表示最多可以爬m个台阶
if(i - j >= 0) dp[i] += dp[i-j];
}
}
return dp[n];
}
边栏推荐
- 47Haproxy集群
- 来看Prada大秀吗?在元宇宙里那种!
- 想通这点,治好 AI 打工人的精神内耗
- 代码随想录笔记_动态规划_70爬楼梯
- LeetCode中等题之比较版本号
- Keithley DMM7510 accurate measurement of ultra-low power consumption equipment all kinds of operation mode power consumption
- 神经网络可视化有3D版本了,美到沦陷!(已开源)
- Is there a problem with the CURRENT_TIMESTAMP(6) function?
- Crypto Gaming: The Future of Gaming
- iTextSharp操作PDF
猜你喜欢

阿里云贾朝辉:云XR平台支持彼真科技呈现国风科幻虚拟演唱会

Chapter9 : De Novo Molecular Design with Chemical Language Models

shell:正则表达式及三剑客grep命令

StarRocks on AWS Review | Data Everywhere Series Event Shenzhen Station ended successfully
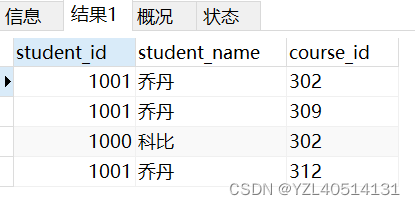
MySQL面试题——MySQL常见查询

LeetCode简单题之合并相似的物品

代码随想录笔记_动态规划_70爬楼梯
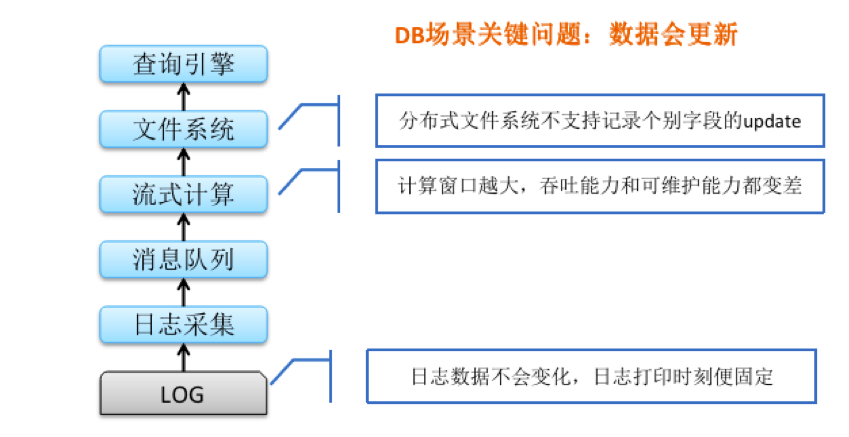
百度用户产品流批一体的实时数仓实践

机器学习实战(2)——端到端的机器学习项目

Nanodlp v2.2/v3.0光固化电路板,机械开关/光电开关/接近开关的接法和系统状态电平设置
随机推荐
动态规划之最长回文子串
Prada, big show?In the yuan in the universe that!
2022年8月中国数据库排行榜:openGauss重夺榜眼,PolarDB反超人大金仓
关于flask中static_folder 和 static_url_path参数理解
解决 idea 单元测试不能使用Scanner
Pod生命周期
Shell:数组
Keithley DMM7510 accurate measurement of ultra-low power consumption equipment all kinds of operation mode power consumption
Nanodlp v2.2/v3.0 light curing circuit board, connection method of mechanical switch/photoelectric switch/proximity switch and system state level setting
跨域的五种解决方案
Deploy the project halfway through the follow-up
线代 | 秒杀方法与技巧
LeetCode中等题之比较版本号
部署项目半途而废后续
【iOS】Organization of interviews
瑞幸「翻身」?恐言之尚早
【数字IC验证进阶】SoC系统验证和IP模块验证的区别及侧重点分析
StarRocks on AWS 回顾 | Data Everywhere 系列活动深圳站圆满结束
48MySQL数据库基础
DNS欺骗-教程详解