当前位置:网站首页>2021-2022-2 ACM集训队每周程序设计竞赛(8)题解
2021-2022-2 ACM集训队每周程序设计竞赛(8)题解
2022-04-23 19:12:00 【ZZXzzx0_0】
A. 21点游戏
题意:
给你三个数A1 , A2 , A3 ,
如果A1 + A2 + A3 >= 22 , 输出 bust
否则输出 win
思路:
模拟
时间复杂度: O 1 O1 O1
#include<bits/stdc++.h>
using namespace std ;
const int N = 1e6 + 10 ;
int main()
{
int a , b , c ;
cin >> a >> b >> c;
int s = a + b + c ;
if(s >= 22) puts("bust") ;
else puts("win") ;
return 0 ;
}
B. 回文游戏
题意:
给你一个字符串S,
你可以修改S的任意一个字符,
问最少需要修改多少次,使得S变成一个回文串。
思路:
双指针
时间复杂度: O n On On
#include<bits/stdc++.h>
using namespace std ;
const int N = 1e6 + 10 ;
char s[N] ;
int main()
{
cin >> s + 1 ;
int n = strlen(s + 1) ;
int res = 0 ;
for(int i = 1 , j = n ; i < j ; i ++ , j --)
{
if(s[i] != s[j]) res ++ ;
}
cout << res ;
return 0 ;
}
C. 好人 or 坏人 ?
题意:
有n个人在玩一个游戏,
这个游戏是这样的,我们将n个人分为好人和坏人,也有可能n个人都是好人或者都是坏人
好人说的话一定是对的,坏人说的话有可能对,也有可能不对。
现在给你每个人对另外一些人的判断,
问好人最多有多少个
思路:
注意到n最多有15个人,每个人要么好人要么坏人,所以暴力枚举所有可能性,时间复杂度为 2 15 2^{15} 215,
这里可以用状态压缩来枚举,或者用dfs枚举。
对每一种情况来说,每个人是好人还是坏人都是已知的。
那么好人说的话一定是对的,如果出现了冲突,则说明这种情况不行。
可以的话,更新一下好人人数即可。
时间复杂度: O ( 2 15 ∗ n 2 ) O(2^{15}*n^{2}) O(215∗n2)
#include <bits/stdc++.h>
using namespace std;
int n,m,x,y,z;
vector<pair<int ,int> > a[20];
int main(){
cin>>n;
for (int i=0;i<n;i++){
cin>>m;
for (int j=0;j<m;j++){
cin>>x>>y;
a[i].push_back(make_pair(x-1,y));
}
}
for (int i=0;i<1<<n;i++){
int f=1;
for (int j=0;j<n;j++){
if (i>>j&1){
for (pair<int,int>k:a[j]){
if ((i>>k.first&1)!=k.second) f=0;
}
}
}
if (f) z=max(z,__builtin_popcount(i));
}
cout<<z<<endl;
return 0;
}
D. 异或和
题意:
给你n个数的数组
a 1 a_1 a1 a 2 a_2 a2 … a n a_n an
求( ∑ i = 1 n − 1 ∑ j = i + 1 n ( a [ i ] ⊕ a [ j ] ) \sum_{i=1}^{n - 1}{\sum_{j=i + 1}^{n}{(a[i] \oplus a[j])}} ∑i=1n−1∑j=i+1n(a[i]⊕a[j])) % ( 1 0 9 10^9 109 + 7)
A ⊕ B A\oplus B A⊕B 表示A异或B , 也表示为(a ^ b)
思路:
位运算需要拆解每一位来看,
我们假设 b [ k ] [ i ] b[k][i] b[k][i]数组表示 a i a_i ai的二进制表示下的第 k k k位是 1 1 1还是 0 0 0
所以我们只需要求出每一位上 ∑ i = 1 n − 1 ∑ j = i + 1 n ( b [ k ] [ i ] ⊕ b [ k ] [ j ] ) \sum_{i=1}^{n - 1}{\sum_{j=i + 1}^{n}{(b[k][i] \oplus b[k][j])}} ∑i=1n−1∑j=i+1n(b[k][i]⊕b[k][j])的值
答案累加上 2 k ∗ ∑ i = 1 n − 1 ∑ j = i + 1 n ( b [ k ] [ i ] ⊕ b [ k ] [ j ] ) 2^k * \sum_{i=1}^{n - 1}{\sum_{j=i + 1}^{n}{(b[k][i] \oplus b[k][j])}} 2k∗∑i=1n−1∑j=i+1n(b[k][i]⊕b[k][j])即可
现在考虑只有一个0/1的数组,如何求 ∑ i = 1 n − 1 ∑ j = i + 1 n ( b [ k ] [ i ] ⊕ b [ k ] [ j ] ) \sum_{i=1}^{n - 1}{\sum_{j=i + 1}^{n}{(b[k][i] \oplus b[k][j])}} ∑i=1n−1∑j=i+1n(b[k][i]⊕b[k][j])
因为只有 0 / 1 0/1 0/1两种情况
偶数个 1 1 1异或等于 0 0 0
奇数个 1 1 1异或等于 1 1 1
因此
∑ i = 1 n − 1 ∑ j = i + 1 n ( b [ k ] [ i ] ⊕ b [ k ] [ j ] ) = 1 的 个 数 ∗ 0 的 个 数 \sum_{i=1}^{n - 1}{\sum_{j=i + 1}^{n}{(b[k][i] \oplus b[k][j])}}=1的个数*0的个数 ∑i=1n−1∑j=i+1n(b[k][i]⊕b[k][j])=1的个数∗0的个数
时间复杂度: O n l o g n Onlogn Onlogn
#include<bits/stdc++.h>
using namespace std ;
#define int long long
const int N = 1e6 + 10 , mod = 1e9 + 7 ;
int res , n , a[N] ;
signed main()
{
cin >> n ;
for(int i = 1 ; i <= n ; i ++)
scanf("%lld" , &a[i]) ;
for(int j = 0 ; j < 60 ; j ++)
{
int cnt = 0 , s ;
for(int i = 1 ; i <= n ; i ++)
{
if(a[i] >> j & 1) cnt ++ ;
}
s = cnt * (n - cnt) % mod ;
for(int i = 0 ; i < j ; i ++) s = s * 2 % mod ;
res += s , res %= mod ;
}
cout << res ;
return 0 ;
}
E. 吃菜
题意:
有n盘菜,每盘菜需要 a i a_i ai的时间去吃,有 b i b_i bi的美味度。
现在有如下规则:
- 点了一盘菜之后,只能将其吃完后才能点下一盘菜。
- t 时刻过后就不能再点菜了,但是依旧可以吃菜。
- 每种菜只能点一次。
最后问最后能够得到的最大美味度是多少。
思路:
如果不考虑第二条规则,很明显是个01背包问题,
我们假设 f [ j ] f[j] f[j]表示时间为 j j j的情况下的最大美味度,
f [ j ] = f [ j − a [ i ] ] + b [ i ] f[j] = f[j - a[i]] + b[i] f[j]=f[j−a[i]]+b[i]
现在考虑加上第二条规则,
也就是说我们可以在 i < t i < t i<t的任意一个时刻美味度加上 b i b_i bi,
显然需要对 a i a_i ai从小到大排序,因为时间长的放在最后去吃的收益最大。
时间复杂度: O n 2 On^2 On2
#include<bits/stdc++.h>
using namespace std ;
#define pll pair<int,int>
#define y second
#define x first
const int N = 1e6 + 10 ;
int n , m ;
pll q[N] ;
int f[N] ;
int res ;
signed main()
{
cin >> n >> m ;
for(int i = 1 ; i <= n ; i ++)
cin >> q[i].x >> q[i].y ;
sort(q + 1 , q + 1 + n) ;
for(int i = 1 ; i <= n ; i ++)
{
for(int j = 0 ; j < m ; j ++)
{
res = max(res , f[j] + q[i].y) ;
}
for(int j = m ; j >= q[i].x ; j --)
{
f[j] = max(f[j] , f[j - q[i].x] + q[i].y) ;
}
}
cout << max(res , f[m]) ;
return 0;
}
F: 矩形
题意:
给定n个坐标系上的点( x i x_i xi, y i y_i yi)
若有如下图所示的三个点(黑点)就可以构造岀一个新的点(红点)。求可构造的点的最多的个数。
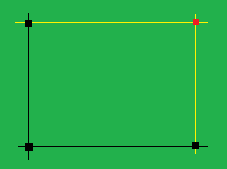
思路:
一个可以操作的地方只要是连通的区域,就可以把这块区域的点填满。
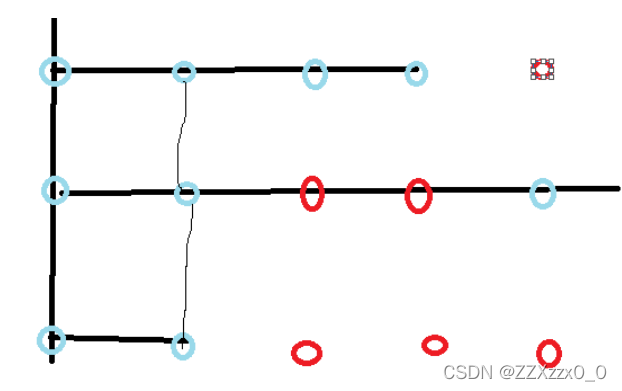
蓝色为已有的点,红色是后来加上的点,可以通过一点点加进来。
只要在这个区域内的,线上的点都可以被填上。
求出每个块内,所有点在的横线和竖线个数,相乘就是所有点。
怎么求有多少个区域呢?我们可以利用并查集,把每个点的横坐标和纵坐标绑在一个集合里,这样以后出现相同竖线的和相同横线的都会被绑进来,形成一个大集合,但是单独计算的时候,只把竖线和横线单独计算。
最后减去已有的点即可。
时间复杂度: O n On On
#include<bits/stdc++.h>
using namespace std ;
const int N = 1e6 + 10 , M = 1e5 ;
int n ;
int p[N] , cnt1[N] , cnt2[N] ;
int find(int x)
{
if(x != p[x]) p[x] = find(p[x]) ;
return p[x] ;
}
int main()
{
cin >> n ;
for(int i = 1 ; i <= N - 10 ; i ++) p[i] = i ;
for(int i = 1 ; i <= n ; i ++)
{
int x , y ;
scanf("%d %d",&x , &y) ;
p[find(x)] = find(y + M) ;
}
for(int i = 1 ; i <= M ; i ++) cnt1[find(i)] ++ ;
for(int i = M + 1 ; i <= 2 * M ; i ++) cnt2[find(i)] ++ ;
long long res = 0 ;
for(int i = 1 ; i <= 2 * M ; i ++) res += (long long)cnt1[i] * cnt2[i] ;
cout << res - n ;
return 0 ;
}
版权声明
本文为[ZZXzzx0_0]所创,转载请带上原文链接,感谢
https://blog.csdn.net/yueshehanjiang/article/details/124265582
边栏推荐
- PyGame tank battle
- Circuit on-line simulation
- 简化路径(力扣71)
- Openlayers 5.0 reload the map when the map container size changes
- Treatment of incomplete display of listview height
- JS to get the local IP address
- Switching power supply design sharing and power supply design skills diagram
- Go 语言 GUI 框架 fyne 中文乱码或者不显示的问题
- js上传文件时控制文件类型和大小
- Practice of Druid SQL and security in meituan review
猜你喜欢
![[报告] Microsoft :Application of deep learning methods in speech enhancement](/img/29/2d2addd826359fdb0920e06ebedd29.png)
[报告] Microsoft :Application of deep learning methods in speech enhancement
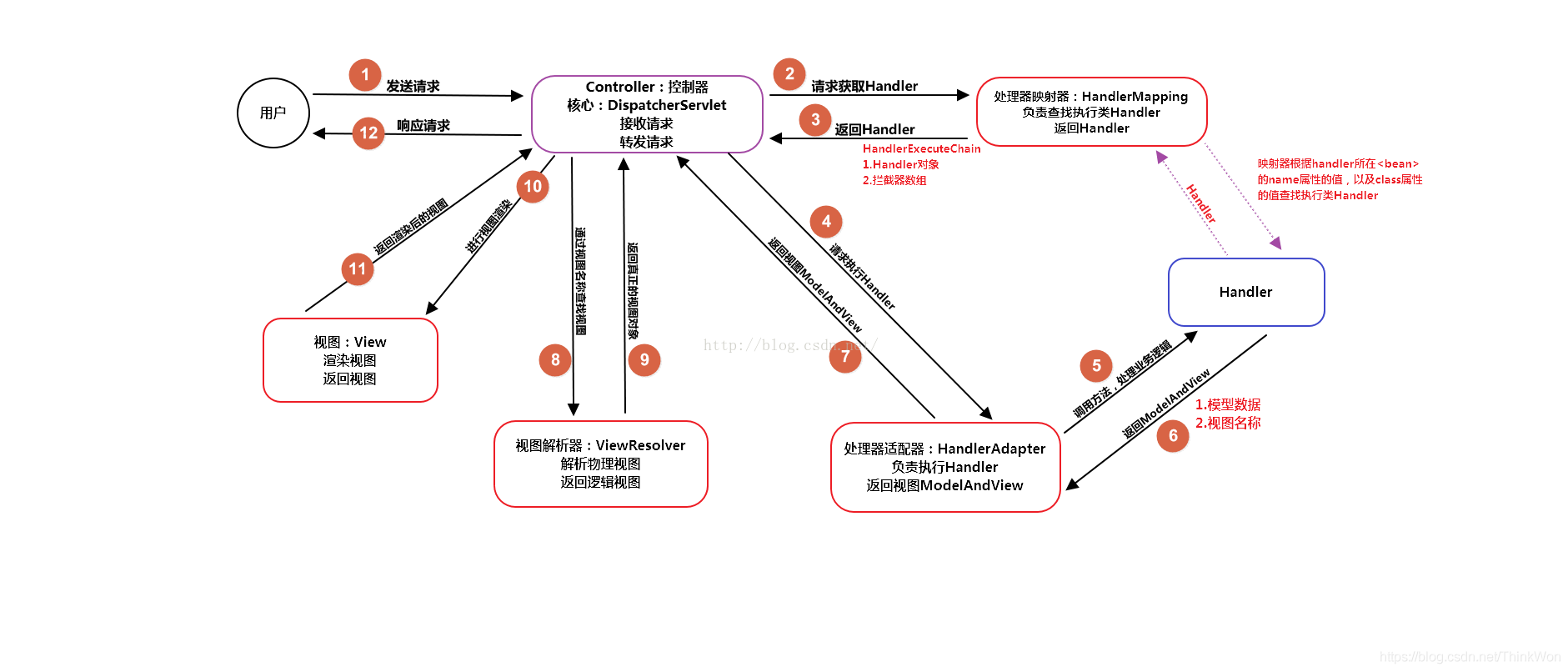
Class loading process of JVM
![[记录]TypeError: this.getOptions is not a function](/img/c9/0d92891b6beec3d6085bd3da516f00.png)
[记录]TypeError: this.getOptions is not a function
Oracle configuration st_ geometry
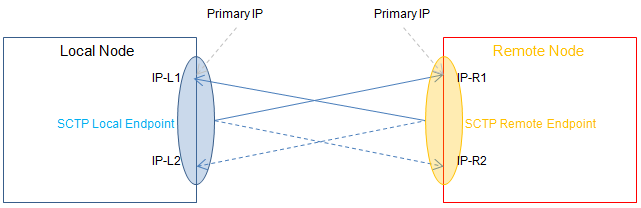
网络协议之:sctp流控制传输协议
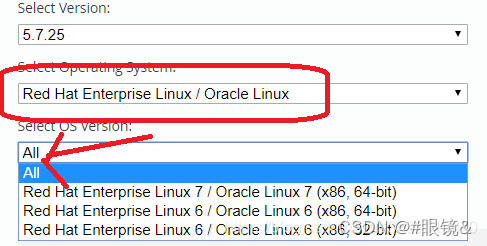
mysql_linux版本的下载及安装详解

Practice of Druid SQL and security in meituan review

Wechat applet part of the mobile phone Preview PDF did not respond

SQL常用的命令
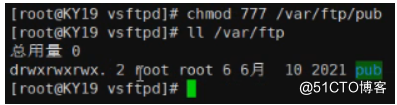
FTP、ssh远程访问及控制
随机推荐
Simple use of viewbinding
SSDB Foundation
Modify the font size of hint in editext
Simplified path (force buckle 71)
【C语言进阶11——字符和字符串函数及其模拟实现(2))】
高层次人才一站式服务平台开发 人才综合服务平台系统
Esp32 drive encoder -- siq-02fvs3 (vscade + IDF)
Esp32 (UART 485 communication) - 485 communication of serial port (3)
mysql通过binlog恢复或回滚数据
Use of content provider
Raspberry pie 18b20 temperature
SSDB foundation 3
openlayers draw矩形
SQL常用的命令
js 计算时间差
剑指 Offer II 116. 省份数量-空间复杂度O(n),时间复杂度O(n)
Accessing private members using templates
Solve the problem of invalid listview Click
c#:泛型反射
mysql_ Download and installation of Linux version