完全背包理论

有N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品都有无限个（也就是可以放入背包多次），求解将哪些物品装入背包里物品价值总和最大。

• 完全背包和01背包问题唯一不同的地方就是，每种物品有无限件。

• 我们知道01背包内嵌的循环是从大到小遍历，为了保证每个物品仅被添加一次。

for(int i = 0; i < weight.size(); i++) {
     // 遍历物品
    for(int j = bagWeight; j >= weight[i]; j--) {
     // 遍历背包容量
        dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
    }
}

• 而完全背包的物品是可以添加多次的，所以要从小到大去遍历，即：

// 先遍历物品，再遍历背包
for(int i = 0; i < weight.size(); i++) {
     // 遍历物品
    for(int j = weight[i]; j <= bagWeight ; j++) {
     // 遍历背包容量
        dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

    }
}

遍历顺序：

• 01背包中二维dp数组的两个for遍历的先后循序是可以颠倒了，一维dp数组的两个for循环先后循序一定是先遍历物品，再遍历背包容量。若先遍历背包容量再嵌套遍历物品则具体如下图（横向一列一列遍历）：

• 当前值由上面的值和左上角的值决定，此种情况遍历某值时左上角的值并不已知，所以不行。

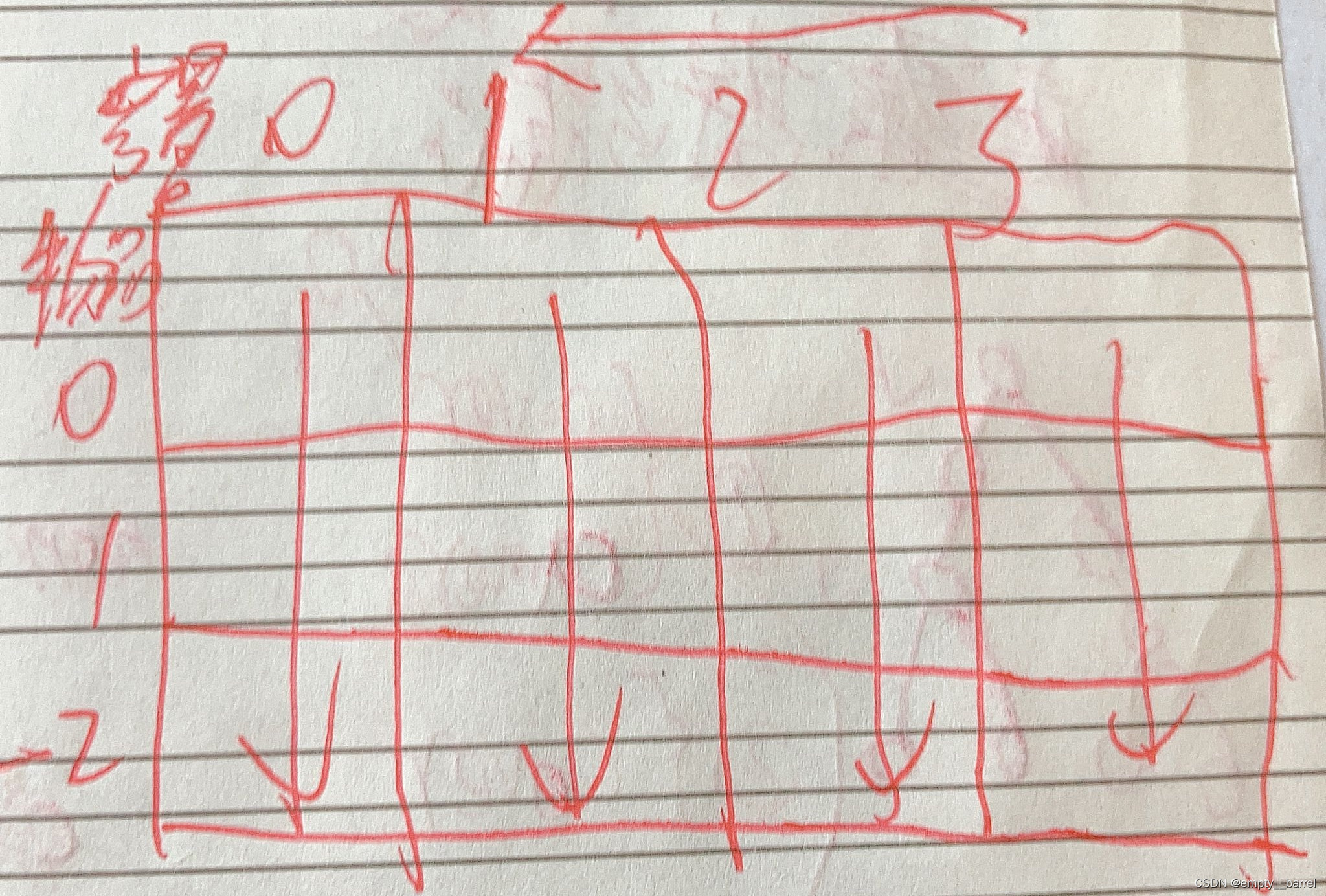
• 在完全背包中，对于一维dp数组来说，其实两个for循环嵌套顺序同样无所谓！因为此时背包重量是按照从小到大来遍历的此时是可以知道左上角的值的。如图（横向一列一列遍历）

代码：
先遍历物品，在遍历背包

void test_CompletePack() {
    
    vector<int> weight = {
    1, 3, 4};
    vector<int> value = {
    15, 20, 30};
    int bagWeight = 4;
    vector<int> dp(bagWeight + 1, 0);
    for(int i = 0; i < weight.size(); i++) {
     // 遍历物品
        for(int j = weight[i]; j <= bagWeight; j++) {
     // 遍历背包容量
            dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
        }
    }
    cout << dp[bagWeight] << endl;
}
int main() {
    
    test_CompletePack();
}

先遍历背包，再遍历物品

void test_CompletePack() {
    
    vector<int> weight = {
    1, 3, 4};
    vector<int> value = {
    15, 20, 30};
    int bagWeight = 4;

    vector<int> dp(bagWeight + 1, 0);

    for(int j = 0; j <= bagWeight; j++) {
     // 遍历背包容量
        for(int i = 0; i < weight.size(); i++) {
     // 遍历物品
            if (j - weight[i] >= 0) dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
        }
    }
    cout << dp[bagWeight] << endl;
}
int main() {
    
    test_CompletePack();
}

两个for循环嵌套顺序适用于不同的题型：
组合不强调元素之间的顺序，排列强调元素之间的顺序。
如果求组合数就是外层for循环遍历物品，内层for遍历背包。
如果求排列数就是外层for遍历背包，内层for循环遍历物品。
例如：
给定不同面额的硬币和一个总金额。写出函数来计算可以凑成总金额的硬币组合数。假设每一种面额的硬币有无限个。
设定总金额为6，面额数组为coins【1,5】
1. 下图一为外层for循环遍历物品，内层for遍历背包
若此时求解dp【6】，dp【6】会被求解两次

• 用1块钱组合成 j 的方法数此时dp【6】 = dp【6】+dp【5】 = 1，关键就在这里此时的dp【5】为1因为是从上到下遍历行的，此时只遍历了第一行前面的值所以这个dp【5】中的序列只是由1组成的原先dp【6】为初始化的dp【6】为0
• 用1块钱和5块钱组合成 j 的方法数即用1块钱的序列组合成 j 的方法数+用有5块钱的序列组合成 j 的方法数 dp【6】= dp【6】+dp【1】= 2

2. 下图二为内层for遍历背包，外层for循环遍历物品
若此时求解dp【6】，dp【6】会被求解两次

• 用1块钱组合成 j 的方法数此时dp【6】 = dp【6】+dp【5】 = 1，**关键就在这里此时的dp【5】为2因为是从左到右遍历列的此时遍历了此列前面的所有列所以这个dp【5】中的序列不仅包含了由值1构成的序列，还包含了由值5构成的序列，**原先dp【6】为初始化的dp【6】为0
• 用1块钱和5块钱组合成 j 的方法数即用1块钱的序列组合成 j 的方法数+用有5块钱的序列组合成 j 的方法数 dp【6】= dp【6】+dp【1】= 2

简单而言，原因就在于

• 当外层for循环遍历物品，内层for遍历背包：计算当前dp的时候，所需要的前面的dp中的序列是仅限于0~当前物品的序列
• 当内层for遍历背包，外层for循环遍历物品：计算当前dp的时候，所需要的前面的dp中的序列是完整的dp是0~物品n的序列

0 ~ n个物品组合成 j 的方法数 = 0 ~ n-1个物品组合成j-coins[n]的方法数+第0~n个有物品n组合成 j 的方法数。这是一个递归，想象时可以递归抽象想象。

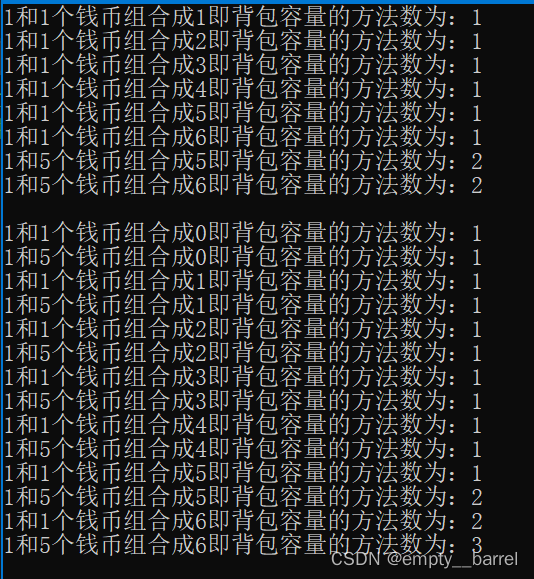
测试代码：

namespace jj01 {
    
    int a() 
        {
    
        vector<int>coins(2);
        coins[0] = 1;
        coins[1] = 5;
        int amount = 6;
        vector<int>dp(7, 0);
        dp[0] = 1;
        for (int i = 0; i < coins.size(); i++) {
     // 遍历物品
            for (int j = coins[i]; j <= amount; j++) {
     // 遍历背包容量
                dp[j] += dp[j - coins[i]];
                cout << coins[0] << "和" << coins[i] << "个钱币组合成" << j << "即背包容量的方法数为：" << dp[j] << endl;
                //有第一个物品组合成 j 的方法数
                //有第二个物品组合成 j 的方法数即没有第二个物品时组合成j-coins[2]的方法数
                //0~n个物品组合成j的方法数 = 0~n-1个物品组合成j-coins[n]的方法数+第0~n个有物品n组合成j的方法数。
            }
        }
        return 0;
    }
}
namespace jj02
{
    
    int a()
    {
    
        vector<int>coins(2);
        coins[0] = 1;
        coins[1] = 5;
        int amount = 6;
        vector<int>dp(7, 0);
        dp[0] = 1;
        for (int j = 0; j <= amount; j++) {
     // 遍历背包容量
            for (int i = 0; i < coins.size(); i++) {
     // 遍历物品
                if (j - coins[i] >= 0) dp[j] += dp[j - coins[i]];
                cout << coins[0] << "和" << coins[i] << "个钱币组合成" << j << "即背包容量的方法数为：" << dp[j] << endl;
                //有第一个物品组合成 j 的方法数
                //有第二个物品组合成 j 的方法数即没有第二个物品时组合成j-coins[2]的方法数
                //0~n个物品组合成j的方法数 = 0~n-1个物品组合成j-coins[n]的方法数+第0~n个有物品n组合成j的方法数。
            }
        }
        return 0;
    }
}
int main() {
    
    jj01::a();
    cout << endl;
    jj02::a();
    return 0;
}