96. Different binary search trees ( secondary )

subject ：

Given an integer n, Seeking for 1 … n How many binary search trees are there for nodes ？

 Example :

 Input : 3
 Output : 5
 explain :
 Given  n = 3,  Altogether  5  Binary search trees with different structures :

   1         3     3      2      1
    \       /     /      / \      \
     3     2     1      1   3      2
    /     /       \                 \
   2     1         2                 3

The reference force buckle gives analysis , Plus my own ideas , I think so .

First , This kind of problem is easy to divide the whole problem into subproblems to solve ; What needs to be solved is the ordered sequence of problems [1, n] The maximum number of binary search trees that can be formed , You can easily get this question from The number of binary trees that each node can form as the root node .

With the simplification of the problem and the definition of the State , Let's see how to get the state transition equation ; Here, refer to the definition of force buckle ：

• F(i, n)： With i Number of different binary search trees for roots (1 <= i <= n)
• G(n): The length is n The number of different binary search trees of the sequence

The meaning of this definition is , have access to F(i, n) As every i Record... For the root node's binary search tree , Finally, the sum of the binary search tree composed of each node as the root is G(n):

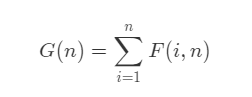
Obviously , The binary search tree composed of a root node has left subtree and right subtree , So if you want to know by i A binary tree formed by the root node , You need to know to i-1 For all possible nodes of the root node of the left subtree , And with n - 1 - (i - 1) All possible nodes of the root node of the right subtree , among n-1 Yes, except i The sum of all nodes except ,i-1 Is the sum of the nodes of the left subtree .

When all nodes of two subtrees know , Why i The state equation of binary tree with root node is ：
F(i, n) = G(i - 1) * G(n - i);
combination **G(n) And F(i, n)** The relationship between , You can get ：

Finally judge the boundary ,n = 1 when G(1) = 1, n = 0 when G(0) =1;

class Solution {
    
public:
    int numTrees(int n) {
    
        if(n == 0){
    
            return 1;
        }
        vector<int> dp(n+1);
        dp[0] = 1;
        for(int i = 1; i <= n; i++){
    
            for(int j = 1; j <= i; j++){
    
                dp[i] += dp[j-1] * dp[i-j];
            }
        }
        return dp[n-1];
    }
};

152. Product maximal subsequence ( secondary )

subject ：

Given an array of integers nums , Find the continuous subsequence with the largest product in a sequence （ The sequence contains at least one number ）.

 Example  1:

 Input : [2,3,-2,4]
 Output : 6
 explain :  Subarray  [2,3]  There is a maximum product  6.
 Example  2:

 Input : [-2,0,-1]
 Output : 0
 explain :  The result can't be  2,  because  [-2,-1]  It's not a subarray .

Again , This problem can be solved by double traversal violence method , The time complexity is (N^2), But through observation , Dynamic programming can still be used for this problem .

What this problem seeks is the Cartesian product of the subsequence with the largest product , Each number must be calculated by the product of the previous number , Therefore, we can take the product of numbers as state . But the product of numbers is different from the sum , If you encounter a negative number after the product is negative, you can Bigger , So you need to maintain two state arrays ,maxDp Maintain the maximum value of the product ,minDp Maintain the minimum value of the product .

At this point, the storage and definition of the state are completed , The next step is to complete the definition of the equation of state ;

When nums[i] >= 0 when

• maxDp[i-1] >= 0, Obviously maxDp[i] = num[i] * maxDp[i-1];
• maxDp[i-1] < 0, maxDp[i] = nums[i];

When nums[i] < 0 when

• minDp[i-1] >= 0, maxDp[i] = nums[i]; // Why not dp[i-1] It will be mentioned later
• minDp[i-1] < 0, maxDp[i] = nums[i] * dp[i-1];

At this time, simplify the above formula ：
maxDp[i] = max(max(maxDp[i-1] * nums[i], minDp[i-1] * nums[i]), nums[i]);
Empathy ：
minDp[i] = min(min(maxDp[i-1] * nums[i], minDp[i-1] * nums[i]), nums[i]);

class Solution {
    
public:
    int maxProduct(vector<int>& nums) {
    
        if(nums.empty()){
    
            return 0;
        }
        if(nums.size() == 1){
    
            return nums[0];
        }   
        int maxNum = nums[0];
        vector<int> maxDp(nums.size(), INT_MIN);
        vector<int> minDp(nums.size(), INT_MAX);
        maxDp[0] = minDp[0] = nums[0];
        for(int i = 1; i < nums.size(); i++){
    
            maxDp[i] = max(max(maxDp[i-1]*nums[i], minDp[i-1]*nums[i]), nums[i]);
            minDp[i] = min(min(maxDp[i-1]*nums[i], minDp[i-1]*nums[i]), nums[i]);
            //  At this time maxNum  Equivalent to dp[i-1]
            maxNum = max(maxNum, maxDp[i]);
        }
        return maxNum;
    }
};

279. Complete square ( secondary )

subject ：

Given a positive integer n, Find some perfect squares （ such as 1, 4, 9, 16, …） Make their sum equal to n. You need to minimize the number of complete squares that make up the sum .

 Example  1:

 Input : n = 12
 Output : 3 
 explain : 12 = 4 + 4 + 4.
 Example  2:

 Input : n = 13
 Output : 2
 explain : 13 = 4 + 9.

Obviously , This problem can still be solved by violence , But dynamic programming can also be used .

What this problem requires is to be less than or equal to N Find the constituent structure with the least number in the complete square of , From this we can refer to knapsack problem .

Description of knapsack problem ： Yes N Items and a capacity for V The backpack . The first i The cost of this item （ Volume , The same below ） yes w[i], The value is val[i]. Figure out which items to pack into a backpack so that the total cost of those items does not exceed the backpack's capacity , And the sum of values is the largest .

When using dynamic programming to solve knapsack problem , Use a two-dimensional array dp[i][v] To indicate yes i The capacity of an item is v The greatest value you can get from your backpack . The equation of state after analysis ：
dp[i] = max(dp[i-1][v] , dp[i-1][v - w[i]] + val[i])
This equation of state is interpreted as ：i - 1 Items with a capacity of v The maximum value you can get under the capacity of your backpack , And i-1 Items with a capacity of v- w[i] Under the capacity of the backpack , With the first i The maximum value you can get by adding items together , The greatest value between the two is the present i The greatest value that an item can constitute

Of course , The equation of state can be reduced to :
dp[i] = max(dp[i], dp[v - w[i]] + val[i]);

After knowing the basic solution of knapsack problem , Square it up again .

The solution can be borrowed from the idea of solving the knapsack problem ,dp[i] Before presentation i The constituent number that can be formed by numbers N The smallest component of the complete square of .

class Solution {
    
public:
    int numSquares(int n) {
    
        if(n == 1 || n == 0){
    
            return 1;
        }
        vector<int> dp(n+1, 0);
        for(int i = 1; i <= n; i++){
    
            dp[i] = i;
            // Get the best choice for weight-i
            for(int j = 1; i-j*j >= 0; j++){
    
            	// state transition equation
                dp[i] = min(dp[i], dp[i-j*j]+1);
            }
        }
        return dp[n];
    }
};

718. Longest repeating subarray ( secondary )

subject ：

Give two arrays of integers A and B , Returns the common of two arrays 、 The length of the longest subarray .

 Example  1:

 Input :
A: [1,2,3,2,1]
B: [3,2,1,4,7]
 Output : 3
 explain : 
 The longest common subarray is  [3, 2, 1].

Can use Longest repeated substring To solve this problem .

Or the method of dynamic programming , Face array A,B, Use a two-dimensional array dp To record the state of traversal . adopt ,dp[i, j] Express A The first of an array of i Number and B The first of an array of j The length of the longest repeating subarray corresponding to the number , Through analysis , Get two situations ：

• A[i] == B[j] , dp[i][j] = dp[i][j-1] + 1; maxLen = max(dp[i][j], maxLen);
• A[i] != B[j], j++(j < B.size) ; i++(i < A.size);

For example, the example shows , adopt dp The array record is ：

0 0 1 2 3
0 1 0 1 2
1 0 0 0 1
0 0 0 0 0
0 0 0 0 0

It can be seen that , The largest substring is 3.

class Solution {
    
public:
    int findLength(vector<int>& A, vector<int>& B) {
    
        if(B.empty()){
    
            return 0;
        }
        vector<vector<int>> dp(A.size()+1, vector<int>(B.size()+1, 0));
        int maxLength = 0;
        for(int i = 1; i <= A.size(); i++){
    
            for(int j = 1; j <= B.size(); j++){
    
                if(A[i-1] == B[j-1]){
    
                    dp[i][j] = dp[i-1][j-1] + 1;
                    maxLength = max(maxLength, dp[i][j]);
                }
            }
        }

        return maxLength;
    }
};