当前位置:网站首页>Brainstorm: Goals and
Brainstorm: Goals and
2022-08-10 15:25:00 【InfoQ】
title
Given an array of non-negative integers, a1, a2, ..., an, and a target number, S.Now you have two symbols + and -.For any integer in the array, you can choose a sign from + or - to prepend.
Returns the number of methods that can make the final array and all the symbols added to the target number S.
Example:
Input: nums: [1, 1, 1, 1, 1], S: 3
Output: 5
Explanation:
-1+1+1+1+1 = 3
+1-1+1+1+1= 3
+1+1-1+1+1 = 3
+1+1+1-1+1 = 3
+1+1+1+1-1 = 3
There are 5 ways to make the final goal sum to 3.
Tips:
- The array is not empty and the length will not exceed 20.
- The initial array sum will not exceed 1000.
- The final result returned is guaranteed to be stored as a 32-bit integer.
Solution ideas
Assuming that the sum of addition is x, then the sum corresponding to subtraction is sum - x.So what we require is x - (sum - x) = S, which can be deduced: x = (S + sum) / 2.
Therefore, this problem can be transformed into, filling capacity x knapsack, there are several ways.
If (S + sum) / 2 is not an integer, there is no solution at this time; and if the target number S is greater than sum, there is also no solution at this time.
This problem needs to be solved by filling the backpack. There are several methods in total, which is a combination problem.
The first step is to determine the dp array and the meaning of the subscript: p[j] means: there are dp[j] methods to fill up a bag with such a large volume of j.
The second step is to determine the recursion formula: the formula for finding a combination problem is generally dp[j] += dp[j - nums[i]].
The third step, dp array initialization: dp[0] must be initialized to 1 during initialization, because dp[0] is the origin of all recursive results in the formula, dp[0]0] = 1, which is also well explained in theory. There is one way to fill a backpack with a capacity of 0, which is to load 0 items.
The fourth step is to determine the traversal order: For the one-dimensional dp traversal of the 01 knapsack problem, nums is placed in the outer loop, target is in the inner loop, and the inner loop is in reverse order.
Code Implementation
class Solution {
public int findTargetSumWays(int[] nums, int target) {
int sum = 0;
for(int i = 0; i < nums.length; i++) sum += nums[i];
if ((target + sum) % 2 != 0) return 0;
int size = (target + sum) / 2;
if(size < 0) size = -size;
int[] dp = new int[size + 1];
dp[0] = 1;
for (int i = 0; i < nums.length; i++) {
for (int j=size; j >= nums[i]; j--) {
dp[j] += dp[j - nums[i]];
}
}
return dp[size];
}
}
Last
- Time complexity: O(n × m), n is a positive number, m is the backpack capacity
- Space complexity: O(m), m is the backpack capacity
边栏推荐
- 【MindSpore易点通机器人-02】设计与技术选型
- 一文让你快速了解大小端概念!
- Pagoda panel open Redis to specify the network machine
- Redis -- Nosql
- const-modified pointer variable (detailed)
- 1004 (tree array + offline operation + discretization)
- scala basics
- Programmer = overtime??- Master the time to master the life
- Oracle数据库备份dmp文件太大,有什么办法可以在备份的时候拆分成多个dmp吗?
- 推荐几款最好用的MySQL开源客户端,建议收藏!
猜你喜欢
随机推荐
Pagoda panel open Redis to specify the network machine
基于inotify实现落盘文件的跨进程实时读写交互
【芯片】人人皆可免费造芯?谷歌开源芯片计划已释放90nm、130nm和180nm工艺设计套件
fastposter v2.9.1 程序员必备海报生成器
Redis -- Nosql
scala集合
Yann LeCun转推:参数减少50倍,性能还更好,MetaAI推出Atlas信息检索模型
MySQL 原理与优化:Update 优化
Oracle数据库备份dmp文件太大,有什么办法可以在备份的时候拆分成多个dmp吗?
Yi Gene|In-depth review: epigenetic regulation of m6A RNA methylation in brain development and disease
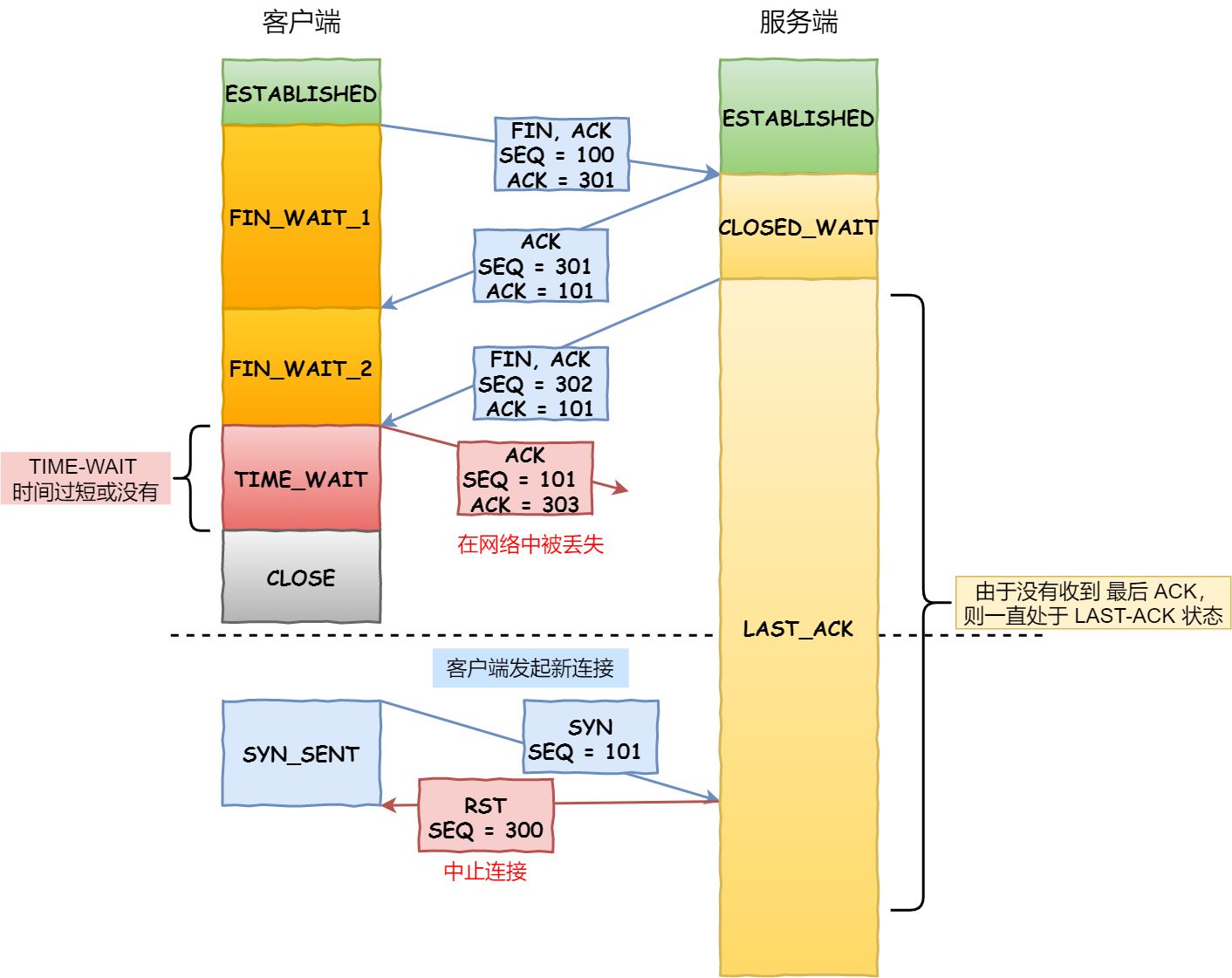
TCP为什么是三次握手和四次挥手?
Go Context基本使用
【数仓设计】企业数仓为什么要进行分层?(六大好处)
Appium进行APP自动化测试
[Data warehouse design] Why should enterprise data warehouses be layered?(six benefits)
$'\r': command not found
容器化 | 在 S3 实现定时备份
头脑风暴:目标和
Mysql statement analysis, storage engine, index optimization, etc.
紫金示例