当前位置:网站首页>快速幂,逆元的求解
快速幂,逆元的求解
2022-08-11 07:49:00 【疯疯癫癫才自由】
875. 快速幂
给定 n
组 ai,bi,pi,对于每组数据,求出 abiimodpi
的值。
输入格式
第一行包含整数 n
。
接下来 n
行,每行包含三个整数 ai,bi,pi
。
输出格式
对于每组数据,输出一个结果,表示 abiimodpi
的值。
每个结果占一行。
数据范围
1≤n≤100000
,
1≤ai,bi,pi≤2×109
输入样例:
2
3 2 5
4 3 9
输出样例:
4
1
1)迭代写法求快速幂
/**
* 1)迭代写法求快速幂
*/
#include <iostream>
using namespace std;
typedef long long LL;
int qmi(int a,int b,int p)
{
int res=1;
while(b)
{
if(b&1)
res=res*(LL)a%p;
b >>=1;
a=(LL)a*a%p;
}
return res;
}
int main()
{
int n;
cin >> n;
while (n -- )
{
int a,b,p;
cin >> a >> b >> p;
cout << qmi(a,b,p) << endl;
}
return 0;
}
2)递归求快速幂
/**
* 2)递归求快速幂
*/
#include <iostream>
using namespace std;
typedef long long LL;
int qmi(int a,int b,int p)
{
if(b==0)
return 1;
if(b&1)
return (LL)a*qmi(a,b-1,p)%p; //注意这里需要强制转换一下,int会溢出
else
{
LL temp=qmi(a,b/2,p);
return temp*temp%p;
}
}
int main()
{
int n;
cin >> n;
while(n--)
{
int a,b,p;
cin >> a >> b >> p;
cout << qmi(a,b,p) << endl;
}
return 0;
}876. 快速幂求逆元
给定 n
组 ai,pi,其中 pi 是质数,求 ai 模 pi
的乘法逆元,若逆元不存在则输出 impossible。
注意:请返回在 0∼p−1
之间的逆元。
乘法逆元的定义
若整数 b,m
互质,并且对于任意的整数 a,如果满足 b|a,则存在一个整数 x,使得 a/b≡a×x(modm),则称 x 为 b 的模 m 乘法逆元,记为 b−1(modm)。
b 存在乘法逆元的充要条件是 b 与模数 m 互质。当模数 m 为质数时,bm−2 即为 b
的乘法逆元。
输入格式
第一行包含整数 n
。
接下来 n
行,每行包含一个数组 ai,pi,数据保证 pi
是质数。
输出格式
输出共 n
行,每组数据输出一个结果,每个结果占一行。
若 ai
模 pi
的乘法逆元存在,则输出一个整数,表示逆元,否则输出 impossible。
数据范围
1≤n≤105
,
1≤ai,pi≤2∗109
输入样例:
3
4 3
8 5
6 3
输出样例:
1
2
impossible
* 假设 a,b,m都是整数,m>1,且ab与1模m同余,则a与b互为模m的逆元。
* 所以当m为质数的时候,a的m-2次方就是a模m的逆元。(费马小定理)。
/**
* 假设 a,b,m都是整数,m>1,且ab与1模m同余,则a与b互为模m的逆元。
* 所以当m为质数的时候,a的m-2次方就是a模m的逆元。(费马小定理)。
*/
#include <iostream>
using namespace std;
typedef long long LL;
int qmi(int a,int b,int p)
{
if(b==0)
return 1;
if(b&1)
return (LL)a*qmi(a,b-1,p)%p; //注意这里需要强制转换一下,int会溢出
else
{
LL temp=qmi(a,b/2,p);
return temp*temp%p;
}
}
int main()
{
int n;
cin >> n;
while (n -- )
{
int a,p;
cin >> a >> p;
if(a%p==0)
cout << "impossible\n";
else
cout << qmi(a,p-2,p) << endl;
}
return 0;
}边栏推荐
猜你喜欢
1101 How many times B is A (15 points)
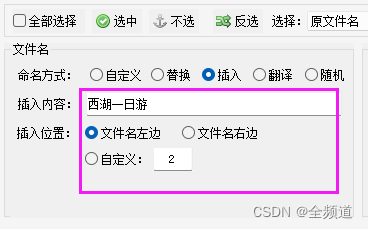
The easiest trick to support quick renaming of various files
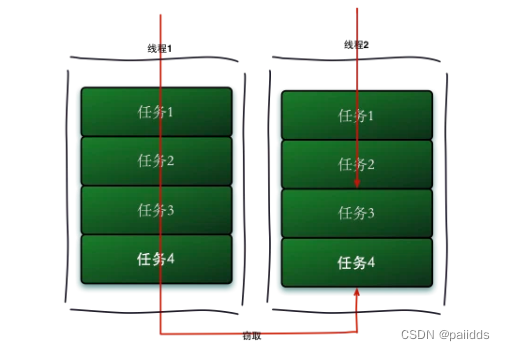
JUC并发编程
关于#sql#的问题:怎么将下面的数据按逗号分隔成多行,以列的形式展示出来

1003 I want to pass (20 points)
租房小程序

求职简历这样写,轻松搞定面试官

1101 B是A的多少倍 (15 分)

About # SQL problem: how to set the following data by commas into multiple lines, in the form of column display
1091 N-自守数 (15 分)
随机推荐
Analysys and the Alliance of Small and Medium Banks jointly released the Hainan Digital Economy Index, so stay tuned!
支持各种文件快速重命名最简单的小技巧
1056 组合数的和 (15 分)
redis operation
Interaction of Pico neo3 in Unity
记录一些遇见的bug——Lombok和Mapstruct的冲突导致,A component required a bean of type ‘com.XXX.controller.converter.
Pico neo3在Unity中的交互操作
年薪40W测试工程师成长之路,你在哪个阶段?
【415. 字符串相加】
excel 透视表 值显示内容 不显示计数
Four startup modes of Activity
1076 Wifi密码 (15 分)
3.2 - classification - Logistic regression
通过记账,了解当月收支情况
关于Excel实现分组求和最全文档
leetcode: 69. Square root of x
【BM87 合并两个有序的数组】
1036 跟奥巴马一起编程 (15 分)
3.1-Classification-probabilistic generative model
几何EX3 功夫牛宣布停售,入门级纯电产品为何总成弃子