当前位置:网站首页>"NIO Cup" 2022 Nioke Summer Multi-School Training Camp 2 DGHJKL Problem Solution
"NIO Cup" 2022 Nioke Summer Multi-School Training Camp 2 DGHJKL Problem Solution
2022-08-11 00:02:00 【Shanhj】
D-Link with Game Glitch
题目大意:
给定 m 个物品合成的方式,求一个最大的合成损耗参数 w ,使得所有物品都无法通过无限合成的方式无限获得.
思路:
就是一个SPFA的简单应用,二分答案,然后用spfaJudge whether the graph is ring can be.double有可能溢出,因此要取log,Is a kind of computing skills.
#include <bits/stdc++.h>
#define mem(a, v) memset(a, v, sizeof(a))
const int N = 1e3 + 5;
using namespace std;
struct edge
{
int to;
double dis;
int next;
} e[4005];
int head[N], idx = 0;
void addedge(int u, int v, double dis)
{
e[++idx].to = v;
e[idx].dis = dis;
e[idx].next = head[u];
head[u] = idx;
}
int n, m, a, b, c, d, cnt[N];
double dis[N], w;
bool inq[N];
bool check() //Check whether there is a positive ring
{
queue<int> q;
for (int i = 1; i <= n; i++)
{
dis[i] = 0;
inq[i] = 1;
cnt[i] = 0;
q.push(i);
}
while (q.size())
{
int u = q.front();
q.pop();
inq[u] = 0;
for (int i = head[u]; i; i = e[i].next)
{
int v = e[i].to;
if (dis[u] + e[i].dis + w > dis[v])
{
dis[v] = dis[u] + e[i].dis + w;
if (!inq[v])
{
q.push(v);
inq[v] = 1;
}
if (++cnt[v] >= n) return true;
}
}
}
return false;
}
signed main()
{
ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
mem(head, 0);
cin >> n >> m;
while (m--)
{
cin >> a >> b >> c >> d;
addedge(b, d, log((double)c / (double)a));
}
double l = 0, r = 1, mid;
while (r - l > 1e-8)
{
mid = (l + r) / 2;
w = log(mid);
if (check())
r = mid;
else
l = mid;
}
printf("%.8lf", mid);
return 0;
}
G-Link with Monotonic Subsequence
题目大意:
构造一个排列,使其 max(lis(p), lds(p)) 最小.
思路:
Conclusion is√nThe size of the group,然后输出.
Guess this conclusion after disproof can,But not guess or difficult to want to.
H-Take the Elevator
题目大意:
n 个人坐电梯,楼高 m ,每个人有起始楼层和目标楼层.电梯有载客量限制 k ,Rise can rise to any layer and drop in at any time,But always drop down to a layer to rise again.电梯每秒运行一层,换方向和上下人不占用时间,问电梯最短运行时间.
思路:
The official answer the following questions more clear hair,But more to write here.
Everyone can be seen as a line,Ontology is a line covering problem,贪心地考虑,Rise when people rise high floor as far as possible to enter the elevator first,Down as far as possible let people down low floor to enter the elevator.Rise to judge whether a person also can enter the condition of the elevator is out of the elevator's floor is not higher than the next one on the floor of the lift,Whereas when falling.然后用setTo maintain everyone out of the elevator and into the elevator can be.
AC代码
#include <bits/stdc++.h>
#define inf 0x3f3f3f3f
using namespace std;
struct seg
{
long long pos1, pos2;
};
bool operator<(seg a, seg b) {
return a.pos2 > b.pos2; }
multiset<seg> up, down, upt, downt;
signed main()
{
ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
long long n, m, k, a, b;
long long ans = 0;
cin >> n >> m >> k;
for (long long i = 0; i < n; i++)
{
cin >> a >> b;
if (a > b) // down
down.insert({
b, a});
else
up.insert({
a, b});
}
while (n)
{
long long maxh = -inf, nowpos;
if (up.size()) maxh = up.begin()->pos2;
if (down.size()) maxh = max(maxh, down.begin()->pos2);
nowpos = up.begin()->pos2;
ans += (maxh - 1) * 2;
while (up.size())
{
while (upt.size() < m)
{
auto it = up.lower_bound({
0, nowpos}); //找到小于nowpos的最大r
if (it == up.end()) break;
upt.insert({
it->pos2, it->pos1});
nowpos = it->pos2;
up.erase(it);
n--;
}
if (!upt.size()) break;
auto it = upt.begin(); //找到最大的l
nowpos = it->pos2;
upt.erase(it);
}
nowpos = down.begin()->pos2;
while (down.size()) //Down the operation and up,Because when the front in the insert will bea和b的位置互换了
{
while (downt.size() < m)
{
auto it = down.lower_bound({
0, nowpos}); //找到最大的l
if (it == down.end()) break;
downt.insert({
it->pos2, it->pos1});
nowpos = it->pos2;
down.erase(it);
n--;
}
if (!downt.size()) break;
auto it = downt.begin(); //找到最大的r
nowpos = it->pos2;
downt.erase(it);
}
}
cout << ans;
return 0;
}
J-Link with Arithmetic Progression

Directly apply linear regression of the board can be.
#include <bits/stdc++.h>
#define inf 0x3f3f3f3f
const long long N = 3e5 + 5;
using namespace std;
namespace GTI //快读模板
{
char gc(void)
{
const long long S = 1 << 16;
static char buf[S], *s = buf, *t = buf;
if (s == t) t = buf + fread(s = buf, 1, S, stdin);
if (s == t) return EOF;
return *s++;
}
long long gti(void)
{
long long a = 0, b = 1, c = gc();
for (; !isdigit(c); c = gc())
b ^= (c == '-');
for (; isdigit(c); c = gc())
a = a * 10 + c - '0';
return b ? a : -a;
}
}
using GTI::gti;
long long num[N];
signed main()
{
long long T;
T = gti();
while (T--)
{
long long n = gti();
long long sxy = 0, sx = 0, sy = 0, sx2 = 0;
long double b, a, ans = 0;
for (long long i = 1; i <= n; i++)
{
num[i] = gti();
sxy += i * num[i];
sx += i;
sy += num[i];
sx2 += i * i;
}
b = ((long double)n * sxy - (long double)sx * sy) / ((long double)n * sx2 - (long double)sx * sx);
a = (long double)sy / n - b * sx / n;
long double ai = a;
for (long long i = 1; i <= n; i++)
{
ai += b;
ans += (num[i] - ai) * (num[i] - ai);
}
printf("%.10lf\n", ans);
}
return 0;
}
K-Link with Bracket Sequence I
题目大意:
给定两种操作(Empty sequence is also legal sequence)
- Give a legitimate brackets sequence on the external set a layer of braces
- The two legal brackets sequence splicing together
构造一个长为m的序列,Make his son can constitute title given sequences,求出方案数.
思路:
Generally this is done with dynamic rules to solve,The equation of the key lies in how to construct and state said.
According to two kinds of operation,Arbitrary sequence beforei个,Left parenthesis is less than the right parenthesis cannot happen,那么dpA dimension can be left parenthesis is more than right parenthesisk个的情况.
So the state is expressed as:
dp[i][j][k]Means take sequence beforei个,With a given sequence oflcs为j,左括号比右括号多kA scheme of the number of
状态转移方程:
At the back of each state we can choose to add left parenthesis or right parenthesis,According to a given sequencej+1A match to decided to shift the way,When you add right parenthesis need to pay attention to the right parenthesis cannot exceed the number of left parenthesis.
if (k) //在dp[i][j][k]的末尾加')'
{
if (a[j + 1] == ')')
dp[i + 1][j + 1][k - 1] = (dp[i + 1][j + 1][k - 1] + dp[i][j][k]) % mod;
else
dp[i + 1][j][k - 1] = (dp[i + 1][j][k - 1] + dp[i][j][k]) % mod;
}
if (a[j + 1] == '(') //给定序列的j+1Who is left parenthesis
dp[i + 1][j + 1][k + 1] = (dp[i + 1][j + 1][k + 1] + dp[i][j][k]) % mod;
else
dp[i + 1][j][k + 1] = (dp[i + 1][j][k + 1] + dp[i][j][k]) % mod;
AC代码:
#include <bits/stdc++.h>
const int N = 205;
using namespace std;
const long long mod = 1e9 + 7;
long long dp[N][N][N]; // dp[i][j][k]表示b的前i个,与a的lcs为j,左括号比右括号多k个
signed main()
{
ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
char a[N];
int T;
cin >> T;
while (T--)
{
int n, m;
cin >> n >> m;
cin >> a + 1;
for (int i = 0; i <= m; i++)
for (int j = 0; j <= min(i, n); j++)
for (int k = 0; k <= i; k++)
dp[i][j][k] = 0;
dp[0][0][0] = 1;
//In order to prevent a repeat of calculation,With a small situation update large situation
//Because of the way bracketing restrictions,Left parenthesis is less than the right parenthesis cannot happen
for (int i = 0; i < m; i++)
{
for (int j = 0; j <= min(i, n); j++)
{
for (int k = 0; k <= i; k++)
{
if (k) //在dp[i][j][k]的末尾加')'
{
if (a[j + 1] == ')')
dp[i + 1][j + 1][k - 1] = (dp[i + 1][j + 1][k - 1] + dp[i][j][k]) % mod;
else
dp[i + 1][j][k - 1] = (dp[i + 1][j][k - 1] + dp[i][j][k]) % mod;
}
if (a[j + 1] == '(') //在dp[i][j][k]的末尾加'('
dp[i + 1][j + 1][k + 1] = (dp[i + 1][j + 1][k + 1] + dp[i][j][k]) % mod;
else
dp[i + 1][j][k + 1] = (dp[i + 1][j][k + 1] + dp[i][j][k]) % mod;
}
}
}
printf("%lld\n", dp[m][n][0]);
}
return 0;
}
L-Link with Bracket Sequence I
题目大意:
有 n 个世界,每个世界是一张简单有向图.从这些世界中选择一个子段进行游戏,规则为从 1 出发,每个世界可以原地不动或经过一条边,到达点 m 即为胜利.要求选出一个尽可能短的子段,使得存在至少一种方案可以胜利.
思路:
Is the topic of a dynamic programming,Because the son to choose the shortest period of,Need to know what must come from one world to another world,最晚可以从哪个世界出发.
Then set the status to:
dp[i][j]表示从第iThe world to the firstj个世界,最晚可以从哪个世界出发
状态转移方程为:
In a world can choose,那么dp[i][j]=dp[k][i]; //k是在iBefore all the world
In a world of mobile,那么dp[i][j]=max(dp[i][j], dp[k][i]); //k是在iBefore and to reach thei的世界
AC代码
#include <bits/stdc++.h>
#define inf 0x3f3f3f3f
const int N = 1e4 + 5;
const int M = 2e3 + 5;
using namespace std;
int dp[2][M], ans = inf;
vector<pair<int, int>> world[N];
signed main()
{
ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
int n, m, l, u, v;
cin >> n >> m;
for (int i = 1; i <= n; i++)
{
cin >> l;
while (l--)
{
cin >> u >> v;
world[i].push_back({
u, v});
}
}
if (m == 1)
cout << "0";
else
{
for (int i = 0; i < M; i++)
dp[0][i] = -inf;
dp[0][1] = 0;
int idx = 0;
for (int i = 1; i <= n; i++)
{
idx ^= 1;
dp[idx][1] = i;
for (int j = 2; j <= m; j++) //In the current world without mobile
dp[idx][j] = dp[idx ^ 1][j];
for (auto e : world[i]) //In the current world mobile
{
dp[idx][e.second] = max(dp[idx ^ 1][e.first], dp[idx][e.second]);
if (e.second == m)
ans = min(ans, i - dp[idx][m]);
}
}
if (ans <= 1e4)
cout << ans;
else
cout << "-1";
}
return 0;
}
边栏推荐
- Qt入门(六)——抽奖系统的实现
- 从0开始设计JVM ,忘记名词跟上思路一次搞懂
- 基于Web的疫情隔离区订餐系统
- 软件测试证书(1)—— 软件评测师
- 11. Custom Converter
- [数据可视化] 图表设计原则
- 5. Lombok
- Software protection scenario of NOR FLASH flash memory chip ID application
- How to quickly grasp industry opportunities and introduce new ones more efficiently is an important proposition
- [Excel知识技能] 将数值格式数字转换为文本格式
猜你喜欢
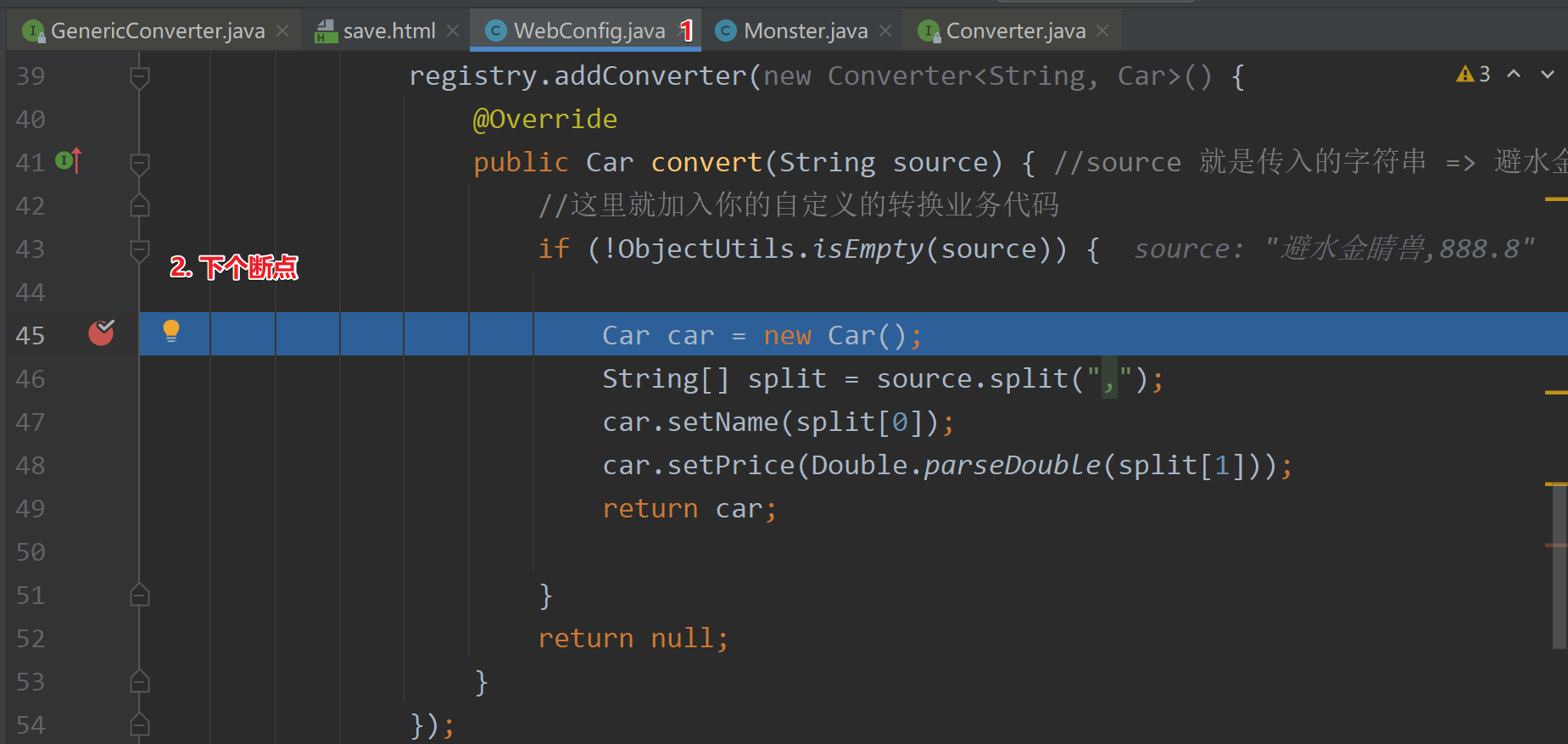
11. Custom Converter
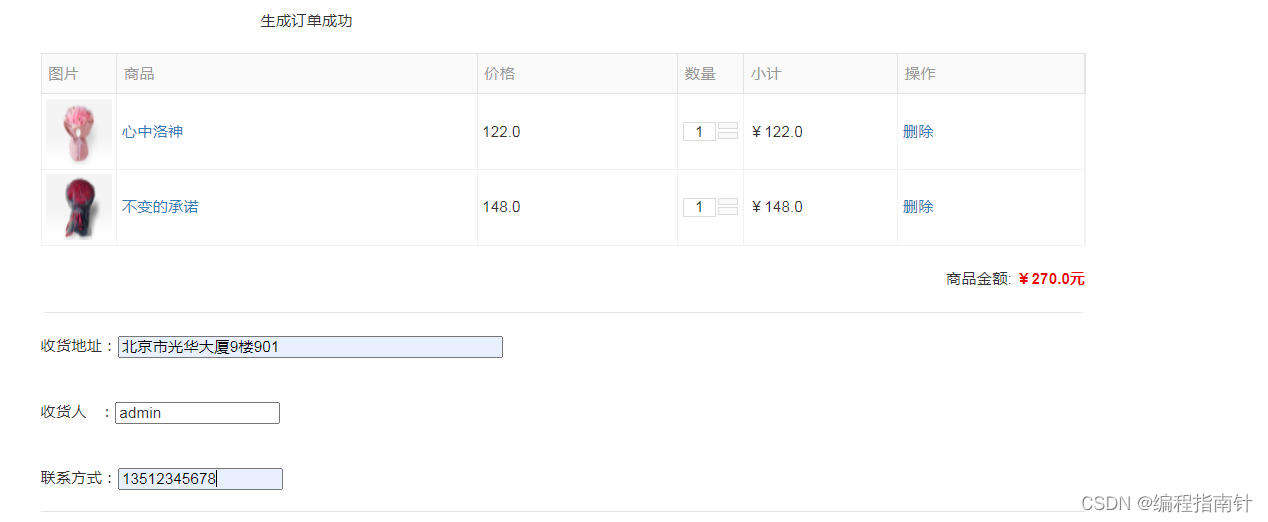
Design and implementation of flower online sales management system
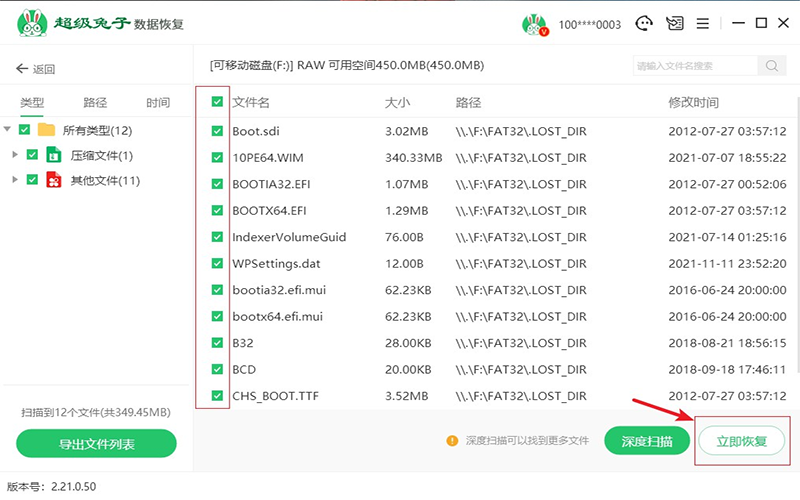
There is no recycle bin for deleted files on the computer desktop, what should I do if the deleted files on the desktop cannot be found in the recycle bin?
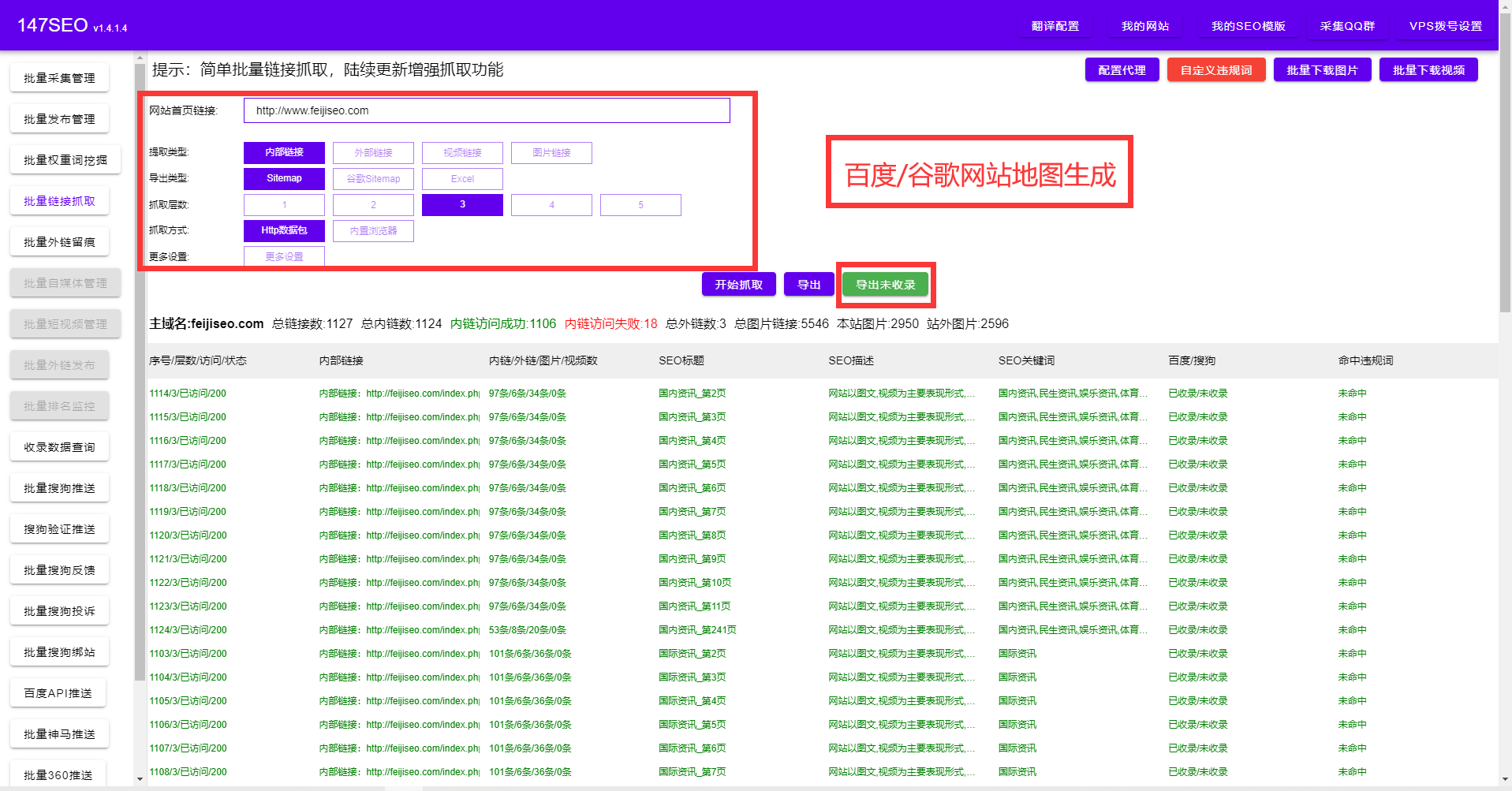
翻译软件哪个准确度高【免费】
从0开始设计JVM ,忘记名词跟上思路一次搞懂
学习Apache ShardingSphere解析器源码(一)

电脑桌面删除的文件回收站没有,电脑上桌面删除文件在回收站找不到怎么办

App regression testing, what are the efficient testing methods?
15. 拦截器-HandlerInterceptor
SAS数据处理技术(一)
随机推荐
The Missing Semester of Your CS Education
Talking about cors
Based on the SSM to reach the phone sales mall system
2. 依赖管理和自动配置
软件测试证书(1)—— 软件评测师
多语种翻译-多语种翻译软件免费
[C language] Detailed explanation of data storage
Starting a new journey - Mr. Maple Leaf's first blog
Special class and type conversion
9. Rest 风格请求处理
地下管廊可视化管理系统搭建
[数据可视化] 图表设计原则
Three-column layout implementation
从0开始设计JVM ,忘记名词跟上思路一次搞懂
Lens filter---about day and night dual-pass filter
Mysql.慢Sql
Jvm.分析工具(jconsole,jvisualvm,arthas,jprofiler,mat)
16. 文件上传
【C语言】初识指针
7. yaml