当前位置:网站首页>假设检验:正态性检验的那些bug——为什么对同一数据,normaltest和ktest会得到完全相反的结果?
假设检验:正态性检验的那些bug——为什么对同一数据,normaltest和ktest会得到完全相反的结果?
2022-08-11 09:39:00 【TingXiao-Ul】
总体分布假设检验原理-卡方检验
对总体分布的假设检验是一种非参数检验,所谓非参数假设检验,即在不确定总体分布的数学形式下,对总体的各种一般性推断。例如,“X服从正态分布”,“X1,X2,…,Xn”同分布等都是非参数假设。对总体分布假设检验的一般形式:设x1,x2,…,xn,来自总体X的样本,据此样本需要检验假设
H0 :
- X的分布函数为F(x)
- 或X的概率密度函数为f(x)
- 或P(Xi)=p,i=1,2,…,k
H1 :X的***不是
例1
掷一颗骰子240次,得点数的频数(观测频数)如下,是否服从均匀分布?
| 出现点数 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 观测频数 | 45 | 36 | 31 | 48 | 42 | 38 |
解:设X表示掷这颗骰子一次出现的点数,其有6种可能取值,若X服从均匀分布,则p(x=i)=1/6,i=1,2,…,6。所以原假设可以写作如下形式:
H0 :X服从均匀分布,即
H0 :P(X=i)=p, i=1,2,…,6;p=1/6
计算卡方统计量公式如下,
分别计算每种取值的观测频数和期望频数(理论频数),得到卡方值,然后查表得到P值,通过P值与置信水平α来判断是否接受原假设,P值越大越容易接受原假设,即认为样本服从均匀分布。
例2
随机抽取到一部分样本x,x为连续数据,问X是否服从正态分布?
解:假设x的概率密度函数为
f ( x ) = 1 2 π σ 2 e − ( x − μ ) 2 2 σ 2 f(x) =\frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x-\mu)^2}{2\sigma^2}} f(x)=2πσ21e−2σ2(x−μ)2
其中μ和σ未知,可以通过极大似然方法对样本估计得到均值和方差的估计值。
有了概率密度函数,就可以设置原假设为:
H0 :X服从正态分布,即
H0 :X具有概率密度函数:
f ( x ) = 1 2 π σ 2 e − ( x − μ ) 2 2 σ 2 f(x) =\frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x-\mu)^2}{2\sigma^2}} f(x)=2πσ21e−2σ2(x−μ)2,
对于连续数据,计算卡方统计量时,需将原数据分箱处理,即转换为分组数据,然后分别计算每组的观测频数和期望频数(理论频数),得到卡方值,查表得到P值,通过P值与置信水平α来判断是否接受原假设,P值越大越容易接受原假设,即认为样本服从正态分布。
卡方检验原理总结
卡方检验是非参数假设检验方法,使用的统计量是卡方。例如做正态性假设检验时,需先根据现有样本,使用极大似然的方法估计出概率密度函数的参数:均值和方差,得到正态分布的概率密度函数f(x)的函数形式,从而可以计算概率值,进而可以计算期望频数(np)来计算卡方统计量,以及P值,通过P值和置信水平的大小比较来判断原假设是是否成立。
步骤:
- 使用极大似然的方法估计概率密度函数的参数值或直接估计概率
- 设置原假设为
H0:概率密度函数=f(x)。
或 P(x)=p
3.计算卡方值,P值,判断是否接受原假设。
P值越大越容易接受原假设,即样本否从某种分布。
正态性检验工具
- k2, p = stats.normaltest(x)
normaltest:非参数假设检验方法,正态性检验时,函数可以自行估计概率密度函数参数值。 - k2, p =scipy.stats.kstest(rvs=x,cdf=‘norm’,args=(0,1))
kstest:非参数假设检验方法,正态性检验时,函数默认均值为0,方差为1 - k2, p =scipy.stats.shapiro(x)
shapiro:非参数假设检验方法,适用于小样本(样本容量<5000)。正态性检验时,函数可以自行估计概率密度函数参数值。??
normaltest、kstest、shapiro三者的原假设均可以为X服从正态分布,P值越小,越容易拒绝原假设,即认为数据不服从正态分布。
例
有如下数据,
import scipy
import numpy as np
rng = np.random.default_rng()
a = rng.normal(0, 1, size=3000)
b = rng.normal(10, 20, size=3000)
c = np.concatenate((a, b))
- normaltest
k2, p = stats.normaltest(b)
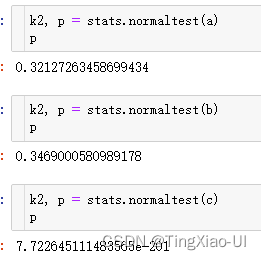
2. kstest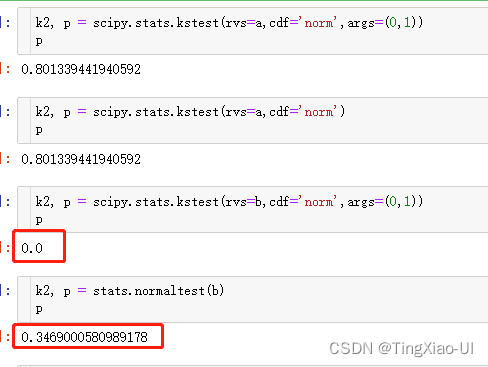
注意:
scipy.stats.normaltest是非参数假设检验总体分布,使用的统计量是卡方。先根据现有样本,使用极大似然的方法估计出均值和方差,得到正态分布的概率密度函数f(x),原假设为H0:概率密度函数=f(x)。而ktest也是非参数检验方法,但是参数估计值默认是均值=0,方差=1或者需要手动输入均值和方差参数。所以,对于同一数据(非标准正态分布),normaltest(估计样本得到参数)和ktest(使用默认参数)得到的结果自然不一样,甚至相反也很正常。也因此,做正态性假设检验时,最好对原数据z-score处理一下,不容易出错。
- 手动填入样本均值、标准差
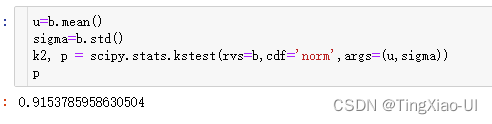
- 对数据做z-score标准化处理

- shapiro

注意
使用shapiro做正态性检验时,有一点要注意,如源代码介绍: shapiro适合检验样本容量小于5000的数据,超过5000时,P值将不在准确。
shapiro适合检验样本容量小于5000的数据,超过5000时,P值将不在准确。
import numpy as np
import pandas as pd
a = rng.normal(0, 1, size=100)
b = rng.normal(10, 6, size=100)
c = np.concatenate((a, b))
d = rng.normal(0, 1, size=6000)
e = rng.normal(10, 5, size=10000)
x=[a,b,c,d,e]
p_list=[]
for da in x:
_,p1=scipy.stats.shapiro(da)
_,p2= scipy.stats.kstest(rvs=da,cdf='norm',args=(da.mean(),da.std()))
_,p3 = stats.normaltest(da)
p_list.append([p1,p2,p3])
df =pd.DataFrame(p_list,index=['a','b','c','d','e'],columns=['shapiro','kstest','normaltest'])
df>0.05
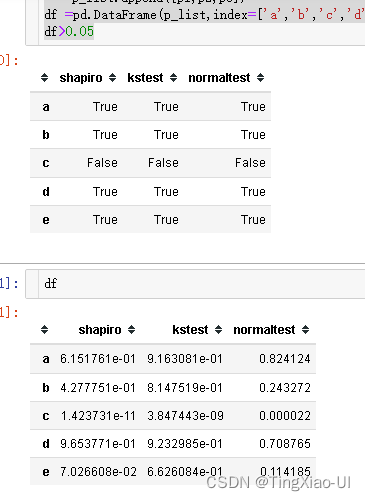
边栏推荐
- Segmentation Learning (loss and Evaluation)
- Huawei WLAN Technology: AC/AP Experiment
- 关于ts中的指针问题call,bind, apply
- 数组、字符串、日期笔记【蓝桥杯】
- 安装ES7.x集群
- Continuous Integration/Continuous Deployment (2) Jenkins & SonarQube
- 淘宝/天猫获得淘宝app商品详情原数据 API
- 软件定制开发——企业定制开发app软件的优势
- idea插件自动填充setter
- Simple interaction between server and client
猜你喜欢
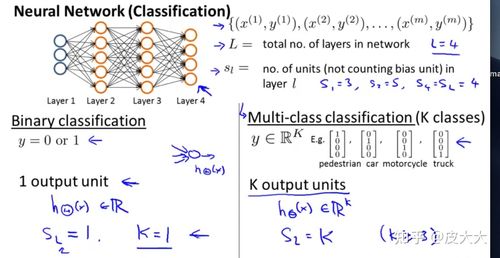
How to determine the neural network parameters, the number of neural network parameters calculation
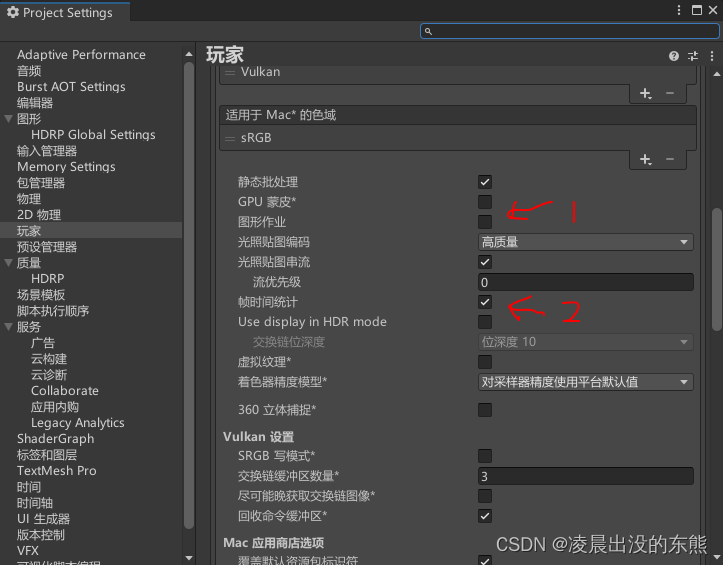
Unity shader test execution time
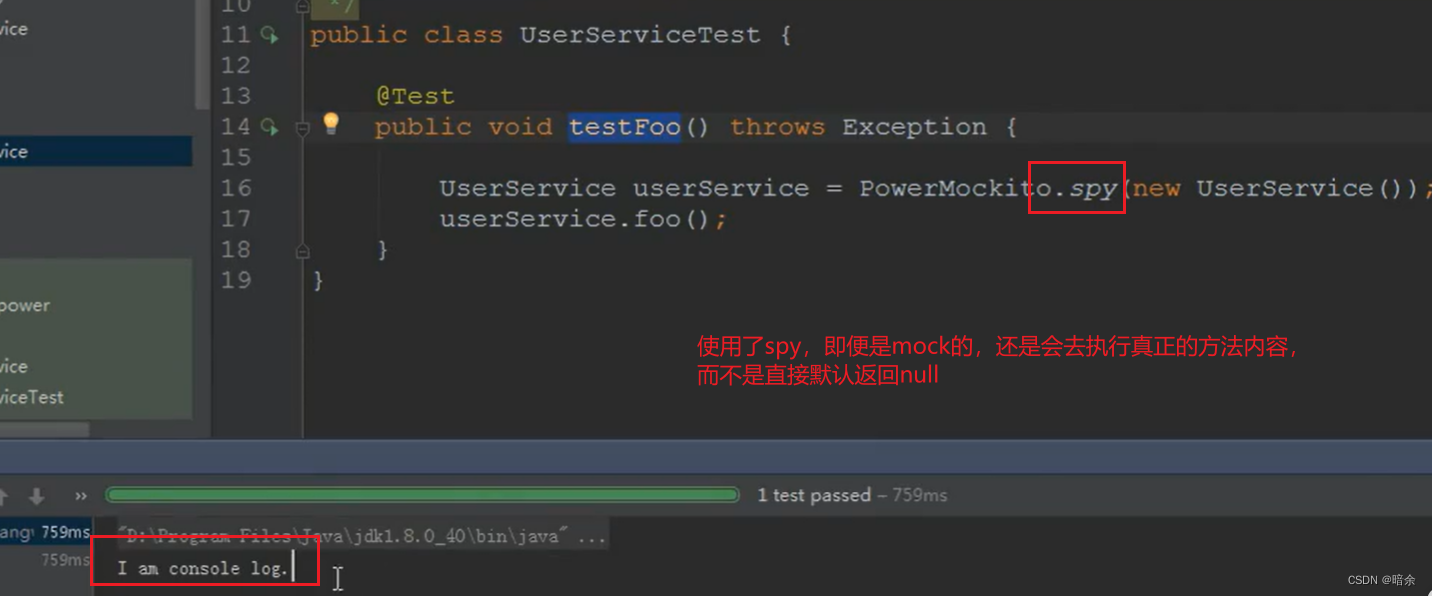
PowerMock for Systematic Explanation of Unit Testing
QTableWidget 使用方法
Continuous Integration/Continuous Deployment (2) Jenkins & SonarQube
WordpressCMS主题开发01-首页制作
![Array, string, date notes [Blue Bridge Cup]](/img/71/242804a93332fc545662b983f3aa2a.png)
Array, string, date notes [Blue Bridge Cup]
力扣题解8/10
如何在移动钱包中搭建一个小程序应用商店

HDRP shader to get shadows (Custom Pass)
随机推荐
Adobe LiveCycle Designer 报表设计器
Audio and video + AI, Zhongguancun Kejin helps a bank explore a new development path | Case study
opencv 制作趣图
力扣题解8/10
Primavera Unifier 高级公式使用分享
Contrastive Learning Series (3)-----SimCLR
仙人掌之歌——大规模高速扩张(1)
IPQ4019/IPQ4029 support WiFi6 MiniPCIe Module 2T2R 2×2.4GHz 2x5GHz MT7915 MT7975
神经痛分类图片大全,神经病理性疼痛分类
OAK-FFC Series Product Getting Started Guide
谁能解答?从mysql的binlog读取数据到kafka,但是数据类型有Insert,updata,
wordpress插件开发02-首页文章自动摘要插件开发
数据中台方案分析和发展方向
HDRP shader gets pixel depth value and normal information
最强大脑(2)
深度学习100例 —— 卷积神经网络(CNN)识别验证码
联想 U 盘装机后出现 start pxe over ipv4
验证拦截器的执行流程
STM32入门开发 LWIP网络协议栈移植(网卡采用DM9000)
Simple interaction between server and client