当前位置:网站首页>Detailed explanation of C language knowledge points -- data types and variables [1] - carry counting system
Detailed explanation of C language knowledge points -- data types and variables [1] - carry counting system
2022-04-23 15:02:00 【VelvetShiki_ Not_ VS】
Carry counting system
in the light of How data is represented in a computer and its arithmetic and logical operations Of ⽅ Law , A carry counting system is proposed , The computer makes ⽤ Machine language ⾔ Namely ⼆ Base bit , except ⼆ There are other hexadecimal digits for ⼈ Generic language ⾔ The base digit of the count , In order to better realize arithmetic ⾔ The interworking of needs to enter ⾏ Hexadecimal conversion .
Basic concepts :
often ⽤ Hexadecimal digits of
1. ⼆ Base number Binary: Only by 0 and 1 Composed of , stay ⼀ individual ⽐ There are only two situations that can be represented on the special bit , On the two into one , The data ends with B or ()2 Express .
2. ⼋ Base number Octal: from 0~7 common 8 A number indicates , Meet ⼋ Into the ⼀, The data ends with ()8 Express .
3. ⼗ Base number Decimal: from 0~9 common 10 A number means , Meet ⼗ Into the ⼀, The data ends with D or ()10 Express .
4. ⼗ Hex Hexadecimal: from 0~9,A,B,C,D,E,F common 16 A number and a word ⺟ constitute , Meet ⼗ 6、 ... and (F) Into the ⼀, The data ends with ()H or 0x Prefix usage .
5. A weight ( Bit weight or weight ): Hexadecimal number the real value corresponding to the position of each value , For integers , The left digit is the hexadecimal multiple of its right adjacent digit ( Such as binary integer , The weight of the left bit is the integer of the right bit 2 times , The decimal system is 10 times ). The position of each number reflects the weight , For any binary weight, the basic formula is as follows :

Hexadecimal digit weight and conversion
• ⼆ Hexadecimal weight table

1. ⼆ Turn into the system ⼗ Base number
according to ⼆ Every... Of the hexadecimal weight table ⼀ Bit corresponding weight and bit weight decimal formula directly convert each ⽐ Special position 1 Add the weights of to get ⼗ Base result .
example : about ⼆ Base number 10010010.110 turn ⼗ Hexadecimal number
According to the right expansion summation method : take ⼆ The hexadecimal number is written as the expansion of the weighted coefficient , According to ⼗ Base addition, direct summation .
1*2^7+1*2^4+1*2^1+1*2^(-1)+1*2^(-2) = 146.75
You can also directly remember each ⼆ Base number ⽐ The weight of the bit to which the special bit belongs is ⽽ Direct additive ( For one byte 8 The rule of binary integer weight of bits is... From right to left 1 2 4 8 16 32 64 128).
2. ⼆ Turn into the system ⼋ Base number
⼋ The system consists of 0~7⼋ A numerical , By every three ⼆ Binary phase combination , Every time Three Can mean 2^3=8 common ⼋ A data in one case .
example : about ⼆ Hexadecimal number 11001111.01111 turn ⼋ Hexadecimal number
According to every three digits ⼀ individual ⼋ Decimal number principle :
⼆ Base number :011 001 111. 011 110
⼋ Base number :3 1 7. 3 6
Be careful , The integer part is less than three digits on the left (⾼ position ) repair 0,⼩ The number of parts is not enough. Three are on the right ( Low position ) repair 0.
3. ⼆ Turn into the system ⼗ Hex
And ⼋ Base is similar to ,⼆ Base digits Every time 4 A for ⼀ Group , Every time 4 Bits can indicate 16 One of these values , Then add the weights of each part .
example :⼆ Hexadecimal number 1111000010.01101
According to every four digits ⼀ individual ⼗ Principle of hex numbers :
Binary system :0011 1100 0010 . 0110 1000
Hexadecimal :3 C 2. 6 8
So the end result is 3C2.68H. Same as ⼋ Base number ⼀ sample , The integer part is not enough. Four digits are on the left (⾼ position ) repair 0,⼩ The number of parts is not enough. Four digits are on the right ( Low position ) repair 0; Every time ⼀ A byte can be divided into two ⼗ Six base number .
• ⼋ Hexadecimal weight
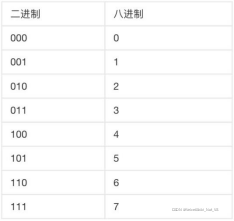
Binary octal correspondence table
1. ⼋ Base number Count 17.36 turn ⼆ Hexadecimal number
According to the table :
⼋ Base number :1 7. 3 6
⼆ Base number :001 111.011 110
You can get ⼆ Hexadecimal number 1111.01111
2. ⼋ Base number Count 251.5 turn ⼗ Base number
Right expansion summation method :
2*8^2+5*8^1+1*8^0+5*8^(-1) = 168.625
3. ⼋ Base number Count 13.40 turn ⼗ Six base number
⼋ Turn into the system ⼗ Hex has no ⼀ Step in place ⽅ Law , It can only be mediated by intermediate hexadecimal numbers , Such as ⼆ Base or ⼗ Hexadecimal number , Then enter again ⾏ transformation .
⼋ Base number :1 3. 4 0
⼆ Base number :001 011. 100 000
⼗ Base number :1*8^1+3*8^0+4*8^(-1) = 11.5( The law of expansion by right )
⼗ Hex :B.8
• ⼗ Hexadecimal weight (Decimalism)
Such as the bits ,⼗ position , One hundred, etc , The weight base of each digital position is 10, That is, the integer part from the lower right to the left ⾼ There are 10^0, 10^1, 10^2 etc. .⼀ Like writing numbers ⽅ The law is :![]()
1. ⼗ Decimal conversion ⼆ Base number ,⼀ There are two kinds of ⽅ Law :
• Integral part Of The method of removing base and taking remainder ,⼩ Count Part of the Rounding by base .
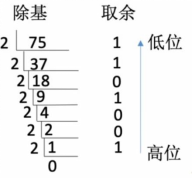
example :⼗ Hexadecimal number 75.3 turn ⼆ Base number
⼗ Base number : Integral part ——75,⼩ Several parts ——0.3
explain : Integers 75 Divide by 2, Will get every time The remainder is written on the right , Be a businessman 0 when , The remainder is from bottom to top In turn ⼆ The low order of hexadecimal to ⾼ position .
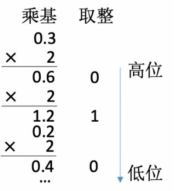
⼩ Count 0.3 Multiply sequentially 2, The results obtained each time Take out the integer bits , Calculation The result is from bottom to top In turn ⼆ Base number ⼩ The low order of the number to ⾼ position . Be careful , because ⼆ The binary weight is fixed , May encounter ⼗ Base number ⼩ The number multiplication base rounding method can never return to 0 The situation of , namely ⼆ The addition of hexadecimal weights can only approximate the ⼩ The number , be accurate ⼆ Base digits ⼀ like only take 5 position .
income ⼆ Hexadecimal integers and ⼩ The final number is 1001011.010
• Rounding up
For the given ⼗ Hexadecimal numbers are not very ⼤, It can be done by ⼆ The digits of the binary digit weight table are pieced together and added ⽽ have to .
example :⼗ Hexadecimal number 260.75 turn ⼆ Base number
No ⽤ Division based remainder method and multiplication based rounding method , Byte lookup ⼆ Hexadecimal weight table , It can be seen from the reference that 1*2^8+1*2^2+1*2^(-1)+1*2^(-2) = 100000100.11
notes : The ⽅ Law The number of calculation digits is not much ⼤ Of ⼗ Turn into the system ⼆ Base number Faster ⽅ then .
2. ⼗ Base number Count 167 turn ⼋ Base number
Integer part ⽤⽅ Law and transformation ⼆ Base integer The method of removing base and taking remainder identical , Just the cardinal part of the divisor r Change into 8.

And ⼆ The decimal remainder is the same , From bottom to top ⼋ Base number ⾼ Bit to low .
3. ⼗ Decimal conversion ⼗ Hex Count two ⽅ Law :
• Integral part divided by 16 Base division and remainder method and ⼩ The multiplication basis rounding method of the number part ( Same as decimal to binary )
example : take ⼗ Hexadecimal number 4966.494 Turn into ⼗ Six base number

explain :
1. Integer part and ⼩ Separate several parts , The integer part is continuously divided by 16, Turn the remainder from bottom to top (⼗ Hex ⾼ Go low ) Write , And meet 16 Into the 1.
2. ⼩ Multiply several parts continuously 16, Take the integer of the result , The integer of the subsequent multiplier returns to 0 The state of , Continue to multiply . Round it up and down ( Or from left to right ) In order of ⼗ Hex goes from low to ⾼ Row , Encountered a problem that cannot be multiplied by an integer ⼩ The number takes the first 6 position .
3. You can also put ⼗ Base to zero ⼆ Base number , Then pass every 4 Position as ⼀ Group converted to ⼗ Hex .
⼗ Hex (Hexadecimalism)
1. ⼗ Hex to ⼆ Base number
example :⼗ Six base number AE86.1 turn ⼆ Base number
⼗ Hex :A E 8 6. 1
⼆ Base number :1010 1110 1000 0110.0001
2. ⼗ Hex to ⼋ Base number
You can start with 16 to decimal , Turn eight or . Sixteen turns ⼆ Re turn ⼋, No, ⼀ Step into place . The specific method is the same as above .
3. ⼗ Hex to ⼗ Base number —— It can be obtained by weighted expansion method
The weighted expansion is consistent with the above method .
Each hexadecimal number represents ⽅ To sum up :

Some material pictures are quoted from the network ,《 Wang Dao's postgraduate entrance examination 》 Series , Invasion and deletion .
Essential knowledge preheating stage , involve C Basic knowledge points , May refer to C Detailed explanation of language knowledge points —— First time to know C Language 【1】_VelvetShiki_Not_VS The blog of -CSDN Blog It's better to eat together ~
Careful arrangement of personal notes , It's not easy to create . If you have any questions, please leave a comment or private letter , If it helps you, please leave a little like before you go ~
版权声明
本文为[VelvetShiki_ Not_ VS]所创,转载请带上原文链接,感谢
https://yzsam.com/2022/04/202204231411217103.html
边栏推荐
- What is the role of the full connection layer?
- 分布式事务Seata介绍
- do(Local scope)、初始化器、内存冲突、Swift指针、inout、unsafepointer、unsafeBitCast、successor、
- go基础 反射
- OC to swift conditional compilation, marking, macro, log, version detection, expiration prompt
- Ffmpeg installation error: NASM / yasm not found or too old Use --disable-x86asm for a clipped build
- 三、梯度下降求解最小θ
- Swift: entry of program, swift calls OC@_ silgen_ Name, OC calls swift, dynamic, string, substring
- Alexnet model
- 科技的成就(二十一)
猜你喜欢
Svn detailed use tutorial
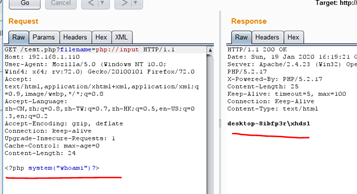
22年了你还不知道文件包含漏洞?
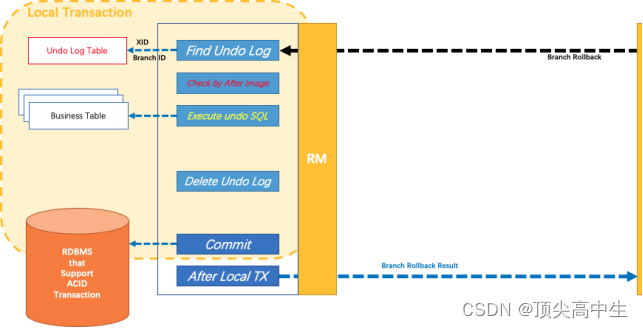
Introduction to distributed transaction Seata
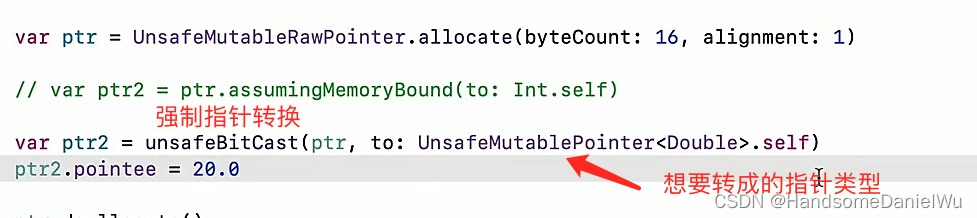
Do (local scope), initializer, memory conflict, swift pointer, inout, unsafepointer, unsafebitcast, success

Swift: entry of program, swift calls OC@_ silgen_ Name, OC calls swift, dynamic, string, substring
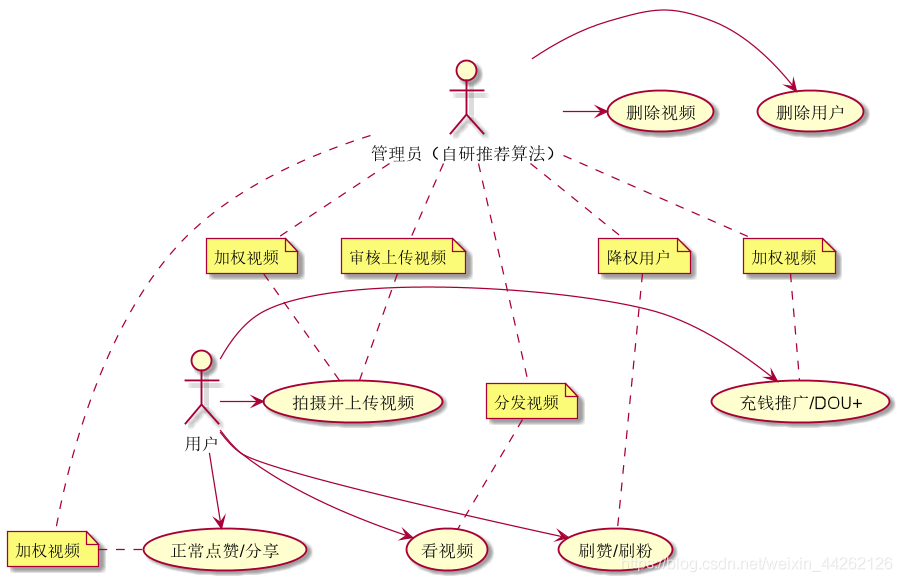
UML project example -- UML diagram description of tiktok
The win10 taskbar notification area icon is missing
《JVM系列》 第七章 -- 字节码执行引擎
What is the effect of Zhongfu Jinshi wealth class 29800? Walk with professional investors to make investment easier
Thinkphp5 + data large screen display effect
随机推荐
我的 Raspberry Pi Zero 2W 折腾笔记,记录一些遇到的问题和解决办法
Difference between like and regexp
I/O复用的高级应用:同时处理 TCP 和 UDP 服务
My raspberry PI zero 2W tossing notes record some problems encountered and solutions
We reference My97DatePicker to realize the use of time plug-in
Swift - literal, literal protocol, conversion between basic data types and dictionary / array
科技的成就(二十一)
Leetcode162 - find peak - dichotomy - array
How to design a good API interface?
Thread synchronization, life cycle
分享 20 个不容错过的 ES6 的技巧
Vous ne connaissez pas encore les scénarios d'utilisation du modèle de chaîne de responsabilité?
剑指 Offer II 019. 最多删除一个字符得到回文(简单)
多语言通信基础 06 go实现grpc的四种数据流模式实现
[NLP] HMM hidden Markov + Viterbi word segmentation
脏读、不可重复读和幻读介绍
Swift:Entry of program、Swift调用OC、@_silgen_name 、 OC 调用Swift、dynamic、String、Substring
编程哲学——自动加载、依赖注入与控制反转
JUC learning record (2022.4.22)
LeetCode149-直线上最多的点数-数学-哈希表