当前位置:网站首页>CFdiv2-Common Number-(奇偶数二分+规律)
CFdiv2-Common Number-(奇偶数二分+规律)
2022-08-10 22:10:00 【可爱美少女】
题意:
就是给你一个函数f(x) = x/2(如果x是偶数),f(x) = x-1(如果x是奇数且不为1)。定义path(15) = [15,14,7,6,3,2,1]。也就是他会走的数字直到为1。然后给你一个k,问你哪个数字在>=k个不同的path中出现过,如果有多个,输出最大的那个数。
思考:
- 既然问最大的,那么肯定可以二分,手推了推发现越小的数字出现在的path越多,那么就肯定是满足单调性的。然后比如check(mid),怎么算mid出现的path?
- 如果x是奇数,那么x包含在path(x),path(2x),path(2x+1),path(4x),path(4x+1),path(4x+2),path(4x+3)。发现最初的起点就是x第一层一个数,然后一直往下面拓展,每拓展一次就是一层的数。
如果x是偶数,那么x包含在path(x),path(x+1),path(2x),path(2x+1),path(2x+2),path(2x+3)。发现最初的起点是[x,x+1]第一层两个数,然后拓展,每次拓展就是一层。 - 刚开始我这样想的时候,感觉你这递归多少次呀,肯定超时了,虽然看起来像log,但是如果暴力dfs去搜每个分支这就是O(n)的。但是如果我每次只存这一层的两个端点呢?那么是不是就log(n)了。为什么每次都是一层呢?画图会发现,这就是一层一层连续的数。
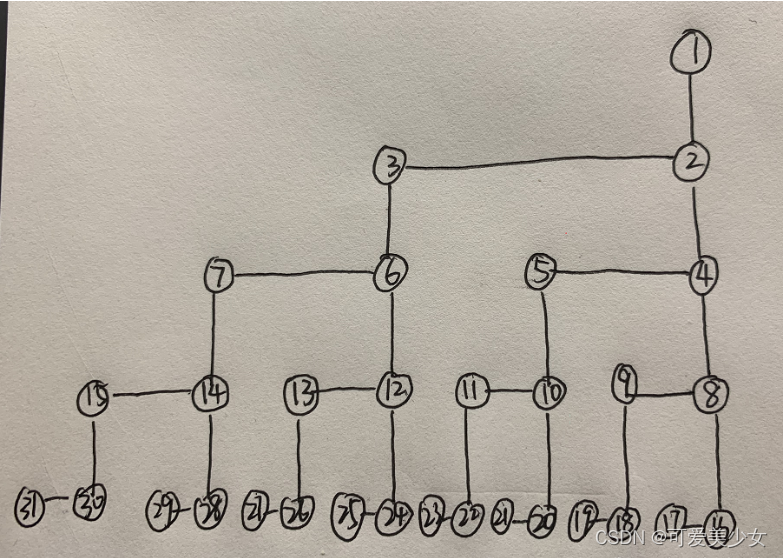
- 然后我就去写了,但是发现不对呀。看了看图发现,并不是整个数都是单调的,而是分奇数偶数的。1>3>5>7…,2>4>6>8…,但是2并不大于3。所以两次二分,一次二分奇数一次二分偶数,每次取最大值就可以了,注意奇数偶数二分的写法。
代码:
#include<bits/stdc++.h>
#define fi first
#define se second
#define pb push_back
#define db double
#define int long long
#define PII pair<int,int >
#define mem(a,b) memset(a,b,sizeof(a))
#define IOS std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
using namespace std;
const int mod = 1e9+7,inf = 1e18;
const int N = 2e5+10,M = 2010;
int T,n,m,k;
int get(int x)
{
queue<PII > q;
if(x&1) q.push({
x,x}); //这一层的左右区间,奇数就自己
else q.push({
x,x+1}); //偶数是两个
int sum = 0;
while(q.size())
{
auto now = q.front();q.pop();
sum += min(n,now.se)-now.fi+1; //这段区间可以加多少数
if(now.fi*2<=n) q.push({
now.fi*2,now.se*2+1}); //如果还可以扩展
}
return sum;
}
bool check(int mid)
{
int sum = get(mid);
return sum>=k;
}
signed main()
{
IOS;
cin>>n>>k;
int maxn = 0;
int l = 1,r = n&1?n:n-1; //初始范围
while(l<=r) //l<=r
{
int mid = (l+r)>>1;
if(mid%2==0) mid--; //如果不是奇数-1
if(check(mid))
{
l = mid+2; //+2
maxn = max(maxn,mid); //答案要在这里面更新
}
else r = mid-2; //-2
}
l = 2,r = n&1?n-1:n;
while(l<=r)
{
int mid = (l+r)>>1;
if(mid%2!=0) mid--;
if(check(mid))
{
l = mid+2;
maxn = max(maxn,mid);
}
else r = mid-2;
}
cout<<maxn;
return 0;
}
总结:
多多思考,画图模拟模拟。
边栏推荐
- 《DevOps围炉夜话》- Pilot - CNCF开源DevOps项目DevStream简介 - feat. PMC成员胡涛
- Redis
- Shell编程之条件语句(二)
- shell脚本循环语句for、while语句
- 2022.8.8 Selected Lectures on Good Topics (Number Theory Field)
- 68: Chapter 6: Develop article services: 1: Content sorting; article table introduction; creating [article] article services;
- LeetCode每日两题02:反转字符串中的单词 (均1200道)
- Why general company will say "go back messages such as" after the end of the interview, rather than just tell the interviewer the result?
- HighTec shortcut keys (Keys) setting location
- Black cats take you learn Makefile article 13: a Makefile collection compile problem
猜你喜欢
QT笔记——QT工具uic,rcc,moc,qmake的使用和介绍

新一代网络安全防护体系的五个关键特征
Addition of linked lists (2)

How to translate financial annual report, why choose a professional translation company?

《DevOps围炉夜话》- Pilot - CNCF开源DevOps项目DevStream简介 - feat. PMC成员胡涛
file IO-buffer
An article to teach you a quick start and basic explanation of Pytest, be sure to read
virtual address space
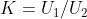
Power system power flow calculation (Newton-Raphson method, Gauss-Seidel method, fast decoupling method) (Matlab code implementation)

爬虫request.get()出现错误
随机推荐
An article to teach you a quick start and basic explanation of Pytest, be sure to read
字节跳动原来这么容易就能进去...
Detailed installation steps and environment configuration of geemap
Shell编程之条件语句(二)
What would happen if disconnecting during the process of TCP connection?
How to be a Righteous Hacker?What should you study?
Spark基础【RDD转换算子】
《DevOps围炉夜话》- Pilot - CNCF开源DevOps项目DevStream简介 - feat. PMC成员胡涛
What is Jmeter? What are the principle steps used by Jmeter?
美味的石井饭
今日睡眠质量记录75分
爬虫request.get()出现错误
Alibaba and Ant Group launched OceanBase 4.0, a distributed database, with single-machine deployment performance exceeding MySQL
MySQL: MySQL Cluster - Principle and Configuration of Master-Slave Replication
STL-stack
GMT,UTC,CST,DST,RTC,NTP,SNTP,NITZ: 嵌入式的时间
商家招募电商主播要考虑哪些内容
Pro-test is effective | A method to deal with missing features of risk control data
黑猫带你学Makefile第13篇:Makefile编译问题合集
shell脚本