目录

一、PCA数据压缩原理

二、样本点中心化

三、计算误差

一、PCA数据压缩原理

二、样本点中心化

        u向量的方向已经确定，我们将样本点映射到u向量上，显然右图的误差要比左图大许多，因此我们就需要先对样本进行中心化，使之分布于原点O附近。即计算所有样本点的均值（x的均值，y的均值），然后将每个样本点减去这个均值，就得到了中心化之后的样本。

三、计算误差

（注意：以下字母加粗表示向量）如下图所示，u为单位向量，表示映射的主方向，x为样本，pijx为x在u上的投影，我们要计算x投影在u上产生的误差e。

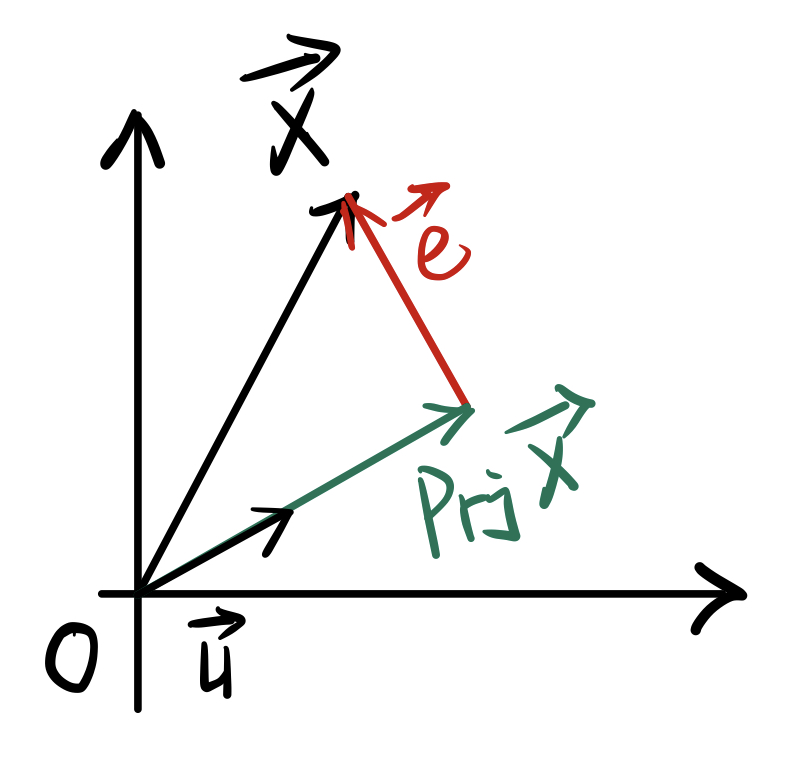
 样本x映射到u上产生的误差e为：

这个式子可以从向量角度理解：我们要计算e，根据向量的加法原则（首尾相连），pijx+e=x。

则得到 e=x-pijx。

pijx即为x在u上的映射，我们表示为：

该公式转化成矩阵的形式如下图所示：

e的模长即为损失的大小：

下面的公式推导不难理解

其中x，u为列向量，故为一个实数，且，不需要进行转置，且可以交换。

得到损失为：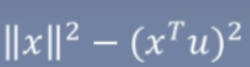

 是固定的，故想要损失降到最低，则需要使最大。

则如下图所示，其中

如果只有一个样本，则，直接求最大值。

但此时有N个样本，那要怎么求最大值呢？

将这N样本进行求和：

 我们令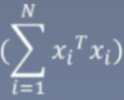为X。

 这样我们的最大化目标就变为：

我们使用拉格朗日条件极值计算最大值（条件为）：

对u求导等于0得到：

对λ求导等于0得到：

满足这两个条件，即可求得最大值，求解n个 λ 和n个u的值，其中λ最大的那个值对应的方向就是最主要的方向，n维降到k维，保留几维就保留几个λ，即λ的个数等于k。

注意：矩阵求偏导相关知识请见：

矩阵求导、几种重要的矩阵及常用的矩阵求导公式_~青萍之末~的博客-CSDN博客_矩阵求导公式大全