当前位置:网站首页>E. Cross Swapping(并查集变形/好题)
E. Cross Swapping(并查集变形/好题)
2022-08-10 14:28:00 【罗gkv】
题意
给定一个n*n的二维矩阵。
执行操作:选择 1 < = k < = n , s w a p ( a [ i ] [ k ] , a [ k ] [ i ] ) , 1 < = i < = n 1<=k<=n,swap(a[i][k], a[k][i]),1<=i<=n 1<=k<=n,swap(a[i][k],a[k][i]),1<=i<=n
比如当n=4,k=3时,转化后如右图所示。
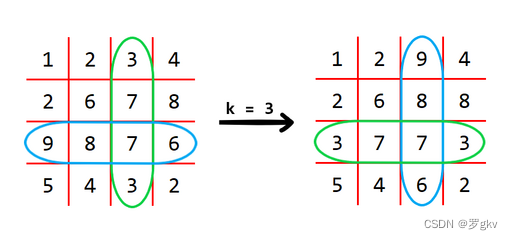
对于上述操作,我们可以执行任意次,也可以是0次。
问,通过执行以上若干次,可以得到的字典序最小的二维数组是啥。
定义二维数组a的字典序为:
将二维数组a映射到一维数组b,映射规则 b[i*n+j] = a[i][j]
二维数组a1字典序小于二维数组a2,
当前仅当它们的映射b1 , b2满足
存在 i , b 1 [ j ] = = b 2 [ j ] , 1 < = j < i ; b 1 [ i ] < b 2 [ i ] i, b1[j] == b2[j], 1<=j<i; b1[i]<b2[i] i,b1[j]==b2[j],1<=j<i;b1[i]<b2[i]
1<=n<=1000
思路
上述操作,本质上就是将a[x][y]和a[y][x]做交换。
当前仅当k取x或y时,会影响到a[x][y]和a[y][x]是否交换。
k可以取1到n。操作k 本质上就是交换第k行和第k列。
对于操作k,有两种选择,要么执行,要么不执行。
因此,我们发现:
- 当操作x和操作y 都执行,或者都不执行时,a[x][y]和a[y][x]没有做交换。
- 当操作x和操作y 一个执行,一个不执行时,a[x][y]和a[y][x]做了交换。
如下图,当前1,2操作都执行后,a[1][2]和a[2][1]没有交换;而只执行1操作,a[1][2]和a[2][1]发生了交换。
抓住上述规律后,我们再研究,怎么获取最小字典序的问题。
由于是对称的,我们只需要考虑一半,这里我们考虑所有元素a[i][j],下标i<=j的场景。
- 如果a[i][j] < a[i][j],那么此时不交换,比如a[1][2] < a[2][1],这个时候交换后,字典序反倒变大了。不交换,则操作i和操作需要同步,要么都执行,要么都不执行。
- 如果a[i][j] > a[i][j],那么此时交换。交换,则操作i和操作需要不同步,一个执行,另一个不执行
- 此外,由于字典序,是按行优先的,我们要行越小的元素,优先考虑交换/不交换。比如我们研究了a[1][2]是否需要交换后,再研究a[2][3]是否交换。因为a[1][2]排位比a[2][3]高。
得到这么些规律,有没有想到一个相关的数据结构–并查集。
- 把每个操作当成一个独立节点,初始时父节点是自己。
- 对于操作需要同号的,我们把它拉到一个集合去,用union操作。
- 对于操作需要异号的,我们也把它拉到一个集合去,但用正负来区分他们异号。
- 根据行优先,列次之,我们一一构建所有的操作边。
- 最终,把集合里边,为正的(负的)操作,去做执行,负的(正的)边不做执行。
详见代码
代码
#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int maxn = 1010;
int n;
int a[maxn][maxn];
int fa[maxn];
// 并查集初始化
void init() {
for (int i = 1; i <= n; ++i) {
fa[i] = i;
}
}
// 并查集查找根节点
int find1(int u) {
if (u < 0) {
// 负号 取反
return -find1(-u);
}
if (u == fa[u]) {
return u;
}
// 查询过程中做合并
return fa[u] = find1(fa[u]);
}
// 并查集 将u, v拉到同个集合 这里u, v可为负数
void union1(int u, int v) {
u = find1(u);
v = find1(v);
if (abs(u) == abs(v)) {
// 已经在同一个集合
return;
}
if (u < 0) {
fa[-u] = -v;
} else {
fa[u] = v;
}
}
void solve() {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= n; ++j) {
scanf("%d", &a[i][j]);
}
}
init();
for (int i = 1; i <= n; ++i) {
for (int j = i; j <= n; ++j) {
if (a[i][j] < a[j][i]) {
// 同号
union1(i, j);
} else if (a[i][j] > a[j][i]) {
// 异号
union1(i, -j);
}
}
}
for (int i = 1; i <= n; ++i) {
fa[i] = find1(i);
if (fa[i] > 0) {
// you can skip > 0, or skip < 0.
continue;
}
for (int j = 1; j <= n; ++j) {
swap(a[i][j], a[j][i]);
}
}
for (int i = 1; i <= n; ++i) {
for (int j = 1; j < n; ++j) {
printf("%d ", a[i][j]);
}
printf("%d\n", a[i][n]);
}
}
int main() {
int t;
// t = 1;
scanf("%d", &t);
while (t--) {
solve();
}
}
/* */
最后
觉得文章不错子,gongzhonghao 关注下 对方正在debug,一起快乐刷题吧~
边栏推荐
猜你喜欢

【Gazebo入门教程】第三讲 SDF文件的静/动态编程建模
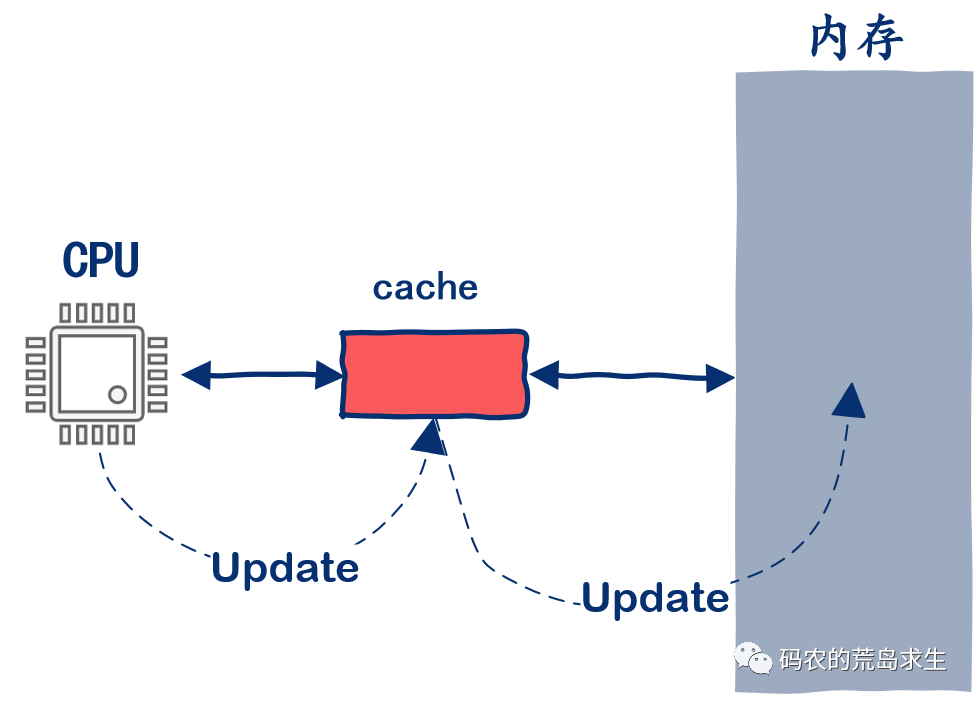
字节终面:CPU 是如何读写内存的?

【MindSpore易点通机器人-02】设计与技术选型
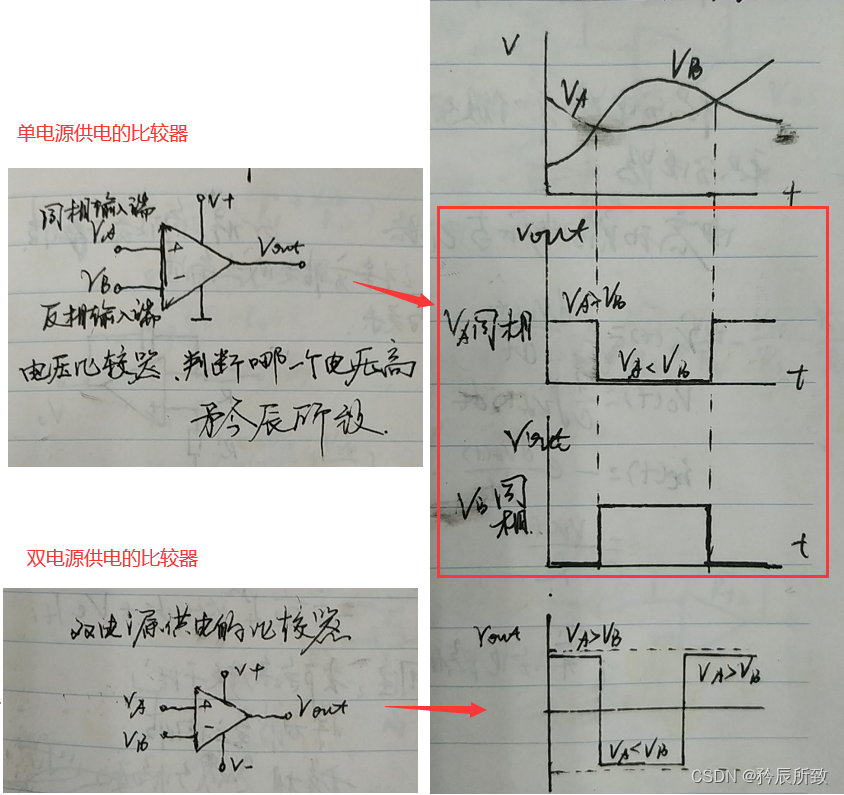
缺少比较器,运放来救场!(运放当做比较器电路记录)

Lack of comparators, op amps come to the rescue!(Op amp is recorded as a comparator circuit)

SQL学习(基础)
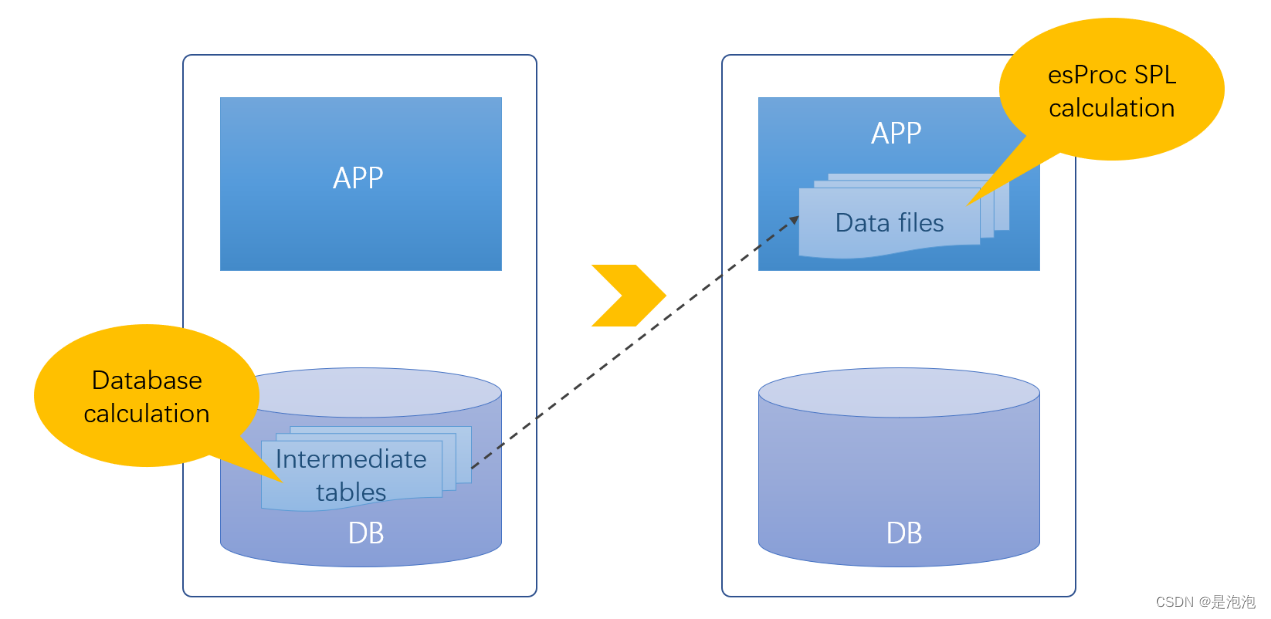
Open source SPL wipes out tens of thousands of database intermediate tables
发送post请求前台无法获取数据
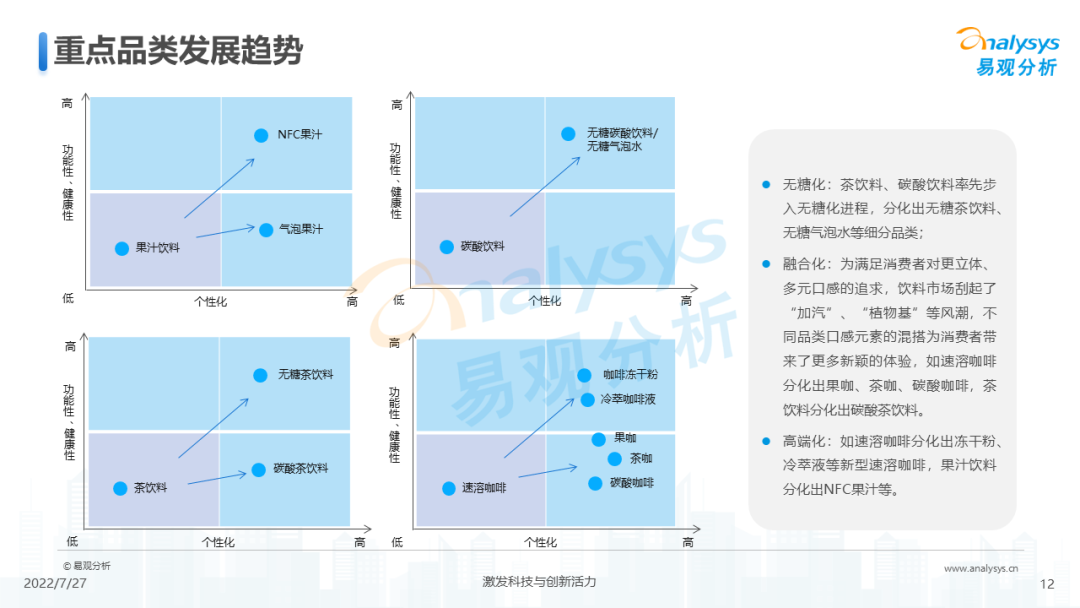
2022年中国软饮料市场洞察
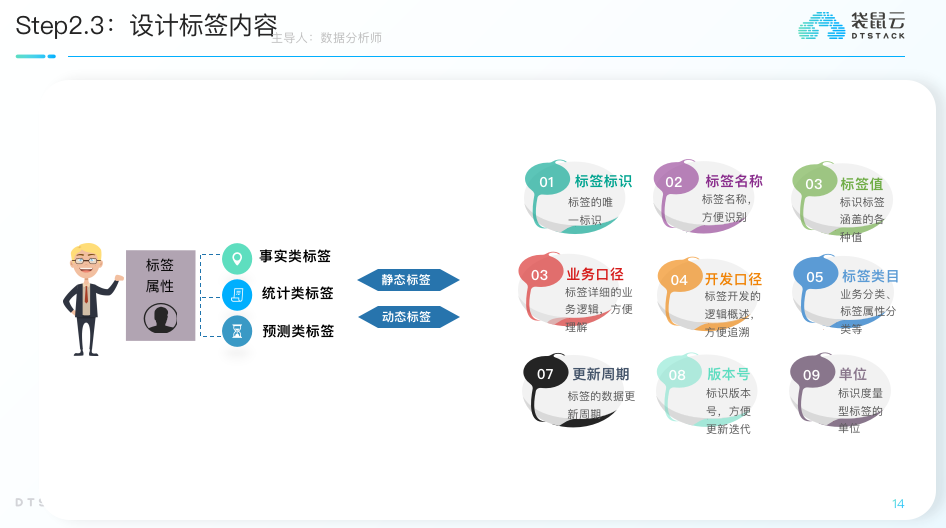
从洞察到决策,一文解读标签画像体系建设方法论
随机推荐
EVE模拟器的使用-带图超详细(学网络用)「建议收藏」
2011年下半年 系统架构设计师 下午试卷 II
How does vue clear the tab switching cache problem?
2022-08-10日报: Swin Transformer作者曹越加入智源,开展视觉基础模型研究
串口服务器调试助手使用教程,串口调试助手使用教程【操作方式】
发送post请求前台无法获取数据
How to code like a pro in 2022 and avoid If-Else
Flask框架——基于Celery的后台任务
数据产品经理那点事儿 一
file system design
PyTorch 多机多卡训练:DDP 实战与技巧
ES5和SE6来实现一个Promise效果
Parallels 将扩展桌面平台产品,以进一步改善在 Mac 上运行 Windows 的用户体验和工作效率
如何完成新媒体产品策划?
舵机内部结及工作原理浅析[通俗易懂]
记录几道整型提升的题目
锂电池技术
The a-modal in the antd component is set to a fixed height, and the content is scrolled and displayed
中学数学建模书籍及相关的视频等(2022.08.09)
sql语句 异常 Err] 1064 – You have an error in your SQL syntax; check the manual that corresponds to your