当前位置:网站首页>Fill in the next right node pointer II of each node [classical hierarchy traversal | regarded as linked list]
Fill in the next right node pointer II of each node [classical hierarchy traversal | regarded as linked list]
2022-04-23 14:52:00 【REN_ Linsen】
Classic level traversal | Treat as a linked list
- Preface
- One 、 Fill in the next right node pointer for each node II
- Two 、 Answer key
-
- 1、 Level traversal
- 2、 Wrong thinking , But some can refer to
- 3、 according to 2 In the wrong thinking, the useful thinking can be improved (hash Record each layer tail node + recursive )
- 4、 utilize next Domain reduces the spatial complexity to O(1)( Also use the wrong method 2 Useful thinking in -- As a linked list )
- summary
- reference
Preface
Growth requires a process , It's not a step up to the sky , What needs continuous improvement idea. This passage LeetCode topic – Fill in the next right node pointer for each node II To think and improve step by step .
besides , You can also learn classic level traversal 、hash + recursive 、 Linked list +dummyNode The use of ( Put the linked list next Use it , Reduce space complexity , After all next The domain takes space .).
One 、 Fill in the next right node pointer for each node II
Two 、 Answer key
1、 Level traversal
// Fill in the next right node pointer for each node II
public class Connect {
/* target: For each node next The pointer points to the right adjacent node of the same layer . M1— Typical hierarchical traversal + layered */
public Node connect(Node root) {
if (null == root) return null;
Queue<Node> que = new LinkedList<>();
que.add(root);
int cnt = 1;
Node pre = null;
while (!que.isEmpty()) {
Node cur = que.poll();
if (cur.left != null) que.add(cur.left);
if (cur.right != null) que.add(cur.right);
if (pre != null) pre.next = cur;
pre = cur;
if (--cnt == 0) {
pre = null;
cnt = que.size();
}
}
return root;
}
// Definition for a Node.
class Node {
public int val;
public Node left;
public Node right;
public Node next;
public Node() {
}
public Node(int _val) {
val = _val;
}
public Node(int _val, Node _left, Node _right, Node _next) {
val = _val;
left = _left;
right = _right;
next = _next;
}
}
}
2、 Wrong thinking , But some can refer to
// Recursive solution
//bug: Thinking problems , This version of the method only provides ideas , It's different .
class Connect2 {
/* target: Recursively the of each node next The pointer points to the right adjacent node of the same layer . Who is the right neighbor node ? 1- If the node is the left child of the parent node , Then its right neighbor node is the right child of its parent node |( When the right child of the parent node is null when ) Parent node next Pointer to the left child or right child of the sibling node ( When the left child is null when ). 2- If the node is the right child of the parent node , Then its right neighbor node is the parent node next The pointer points to the node's left child node or right child node ( When the left child is empty ). Recursive flags -- The same sub problem comes out -- The above two sub problems . M2- Recursive preamble traversal , And then set it according to the situation next Pointer pointing . Recursion requires parent The pointer , Current node , Then cooperate with judgment to complete 2 How to deal with the situation . */
public Node connect(Node root) {
// Recursive processing next The pointer .
dfs(null, root);
// Directly return to the root node after processing .
return root;
}
/** * Recursive processing next The pointer * bug: When parent Not for null, But both of his children are null The situation of , Need to keep while Looking for the next sibling . * * @param parent Parent node * @param root Current node */
private void dfs(Node parent, Node root) {
// If the current node passed in is root, that next There's nothing to set up , You don't have to go down recursively next, After all null 了 .
if (root == null) return;
//1- situation 1-- Left child , Need to put next Point to the right child of the parent node .( When the right child of the parent node is null when ) Parent node next Pointer to the left child or right child of the sibling node ( When the left child is null when ).
// The current node may be the root node , So we need to avoid parent by null The situation of , In fact, you can also divide the tree into two subtrees for recursion , So it won't show up parent by null The situation of .
if (parent != null && parent.left == root) {
if (parent.right != null || parent.next == null)
root.next = parent.right;
else if (parent.next.left != null)
root.next = parent.next.left;
else {
Node next = parent.next;
while (next != null && next.left == null && next.right == null) next = next.next;
root.next = next == null ? null : next.left != null ? next.left : next.right;
}
}
//2- situation 2-- The situation of the right child , Need to put next Point to parent node next The pointer points to the left child of the sibling node | The right child ( The left child is null when ).
// notes : You need to judge whether the sibling node does not exist , Yes null.
if (parent != null && parent.right == root && parent.next != null) {
if (parent.next.left != null) root.next = parent.next.left;
else {
Node next = parent.next;
while (next != null && next.left == null && next.right == null) next = next.next;
root.next = next == null ? null : next.left != null ? next.left : next.right;
}
}
// Start recursive settings next.
dfs(root, root.left);
dfs(root, root.right);
}
// Definition for a Node.
class Node {
public int val;
public Node left;
public Node right;
public Node next;
public Node() {
}
public Node(int _val) {
val = _val;
}
public Node(int _val, Node _left, Node _right, Node _next) {
val = _val;
left = _left;
right = _right;
next = _next;
}
}
}
3、 according to 2 In the wrong thinking, the useful thinking can be improved (hash Record each layer tail node + recursive )
// Method 2: improve : Record the of each layer pre node , Encounter a node , Place the of this layer pre Node extraction , If pre==null, It doesn't matter , otherwise pre.next = cur node. The last update pre Is the current node .
//M3--hash coordination level Layer records the of the layer linked list tailNode + Set the name of the linked list next + Update the list of tail Point to , That is, update pre Point to .
class Connect3 {
// Method 2: improve : Record the of each layer pre node , Encounter a node , Place the of this layer pre Node extraction , If pre==null, It doesn't matter , otherwise pre.next = cur node. The last update pre Is the current node .
//M3--hash coordination level Layer records the of the layer linked list tailNode + Set the name of the linked list next + Update the list of tail Point to , That is, update pre Point to .
public Node connect(Node root) {
// Recursive processing next The pointer .
dfs(root, 1);
// Directly return to the root node after processing .
return root;
}
Map<Integer, Node> hash = new HashMap<>();
/** * coordination hashMap Recursively handle the connection of each layer of linked list . * * @param root * @param level */
private void dfs(Node root, int level) {
// If the current node passed in is root, that next There's nothing to set up , You don't have to go down recursively next, After all null 了 .
if (root == null) return;
// Set the new name of the linked list of this layer tail
Node tail = hash.get(level);
if (null != tail) tail.next = root;
// to update tail
hash.put(level, root);
// Start recursively setting the linked list of each layer next
dfs(root.left, level + 1);
dfs(root.right, level + 1);
}
// Definition for a Node.
class Node {
public int val;
public Node left;
public Node right;
public Node next;
public Node() {
}
public Node(int _val) {
val = _val;
}
public Node(int _val, Node _left, Node _right, Node _next) {
val = _val;
left = _left;
right = _right;
next = _next;
}
}
}
4、 utilize next Domain reduces the spatial complexity to O(1)( Also use the wrong method 2 Useful thinking in – As a linked list )
/* Inspired by method 3 , In fact, each layer can be treated as a linked list . notes : See people say ,next similar B+ Treelike next The pointer , When the database search scope , It only needs logN Determine the starting point , then next Take the nodes in the following range . notes : Is that everyone has next, Make good use of next, Then you know all nodes of the upper layer , This avoids using queues to know all nodes in the upper layer . total ; next Pointer benefits : 1- adopt next Can get all current nodes , So as to get the next layer of ordered nodes , Is a queue +Node(left,right) substitute , namely Queue+Node(left,right) == Node(left,right,next). It is a bit like the merging space complexity of linked list O(1) equally . 2- adopt next coordination Search tree O(logN) Find the starting node , So as to quickly determine the scope , Application scenarios --SQL Of range Inquire about . Not from root Start looking again . */
class Connect4 {
/* M4- According to the of the upper linked list node left and right To create a lower level list , Each floor is set with dummyNode Unified operation . When the current list is an empty linked list , End processing ! */
public Node connect(Node root) {
Node dummyPre = new Node();
dummyPre.next = root;
Node dummyCur = new Node();
Node p1 = dummyPre, p2 = dummyCur;
while (p1.next != null) {
Node pre = p1.next;
if (pre.left != null) {
p2.next = pre.left;
p2 = p2.next;
}
if (pre.right != null) {
p2.next = pre.right;
p2 = p2.next;
}
p1 = p1.next;
if (p1.next == null) {
p1 = dummyCur;
dummyCur = new Node();
p2 = dummyCur;
}
}
// Directly return to the root node after processing .
return root;
}
// Definition for a Node.
class Node {
public int val;
public Node left;
public Node right;
public Node next;
public Node() {
}
public Node(int _val) {
val = _val;
}
public Node(int _val, Node _left, Node _right, Node _next) {
val = _val;
left = _left;
right = _right;
next = _next;
}
}
}
summary
1) Level traversal :Queue + cnt Count
2) Binary tree itself is a recursive structure , Recursive traversal is its foundation , So recursive +hash Record each layer tail Node problem solving .
3) Using linked list next Domain , Let it take up a space , Play to reduce the use of two spaces .
4)next benefits ,
1- adopt next Can get all current nodes , So as to get the next layer of ordered nodes , Is a queue +Node(left,right) substitute , namely Queue+Node(left,right) == Node(left,right,next).
It is a bit like the merging space complexity of linked list O(1) equally .
2- adopt next coordination Search tree O(logN) Find the starting node , So as to quickly determine the scope , Application scenarios –SQL Of range Inquire about . Not from root Start looking again .
reference
[1] LeetCode Fill in the next right node pointer for each node II
版权声明
本文为[REN_ Linsen]所创,转载请带上原文链接,感谢
https://yzsam.com/2022/04/202204231450574564.html
边栏推荐
猜你喜欢
Progress in the treatment of depression

Swift - literal, literal protocol, conversion between basic data types and dictionary / array
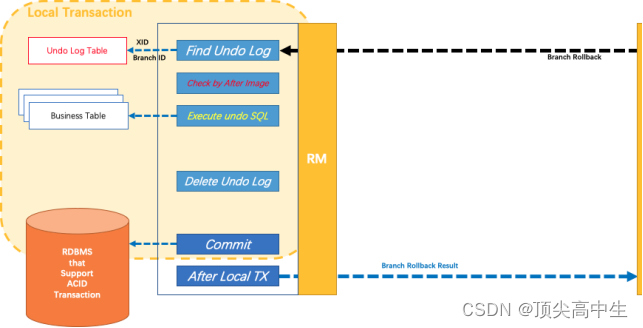
分布式事务Seata介绍
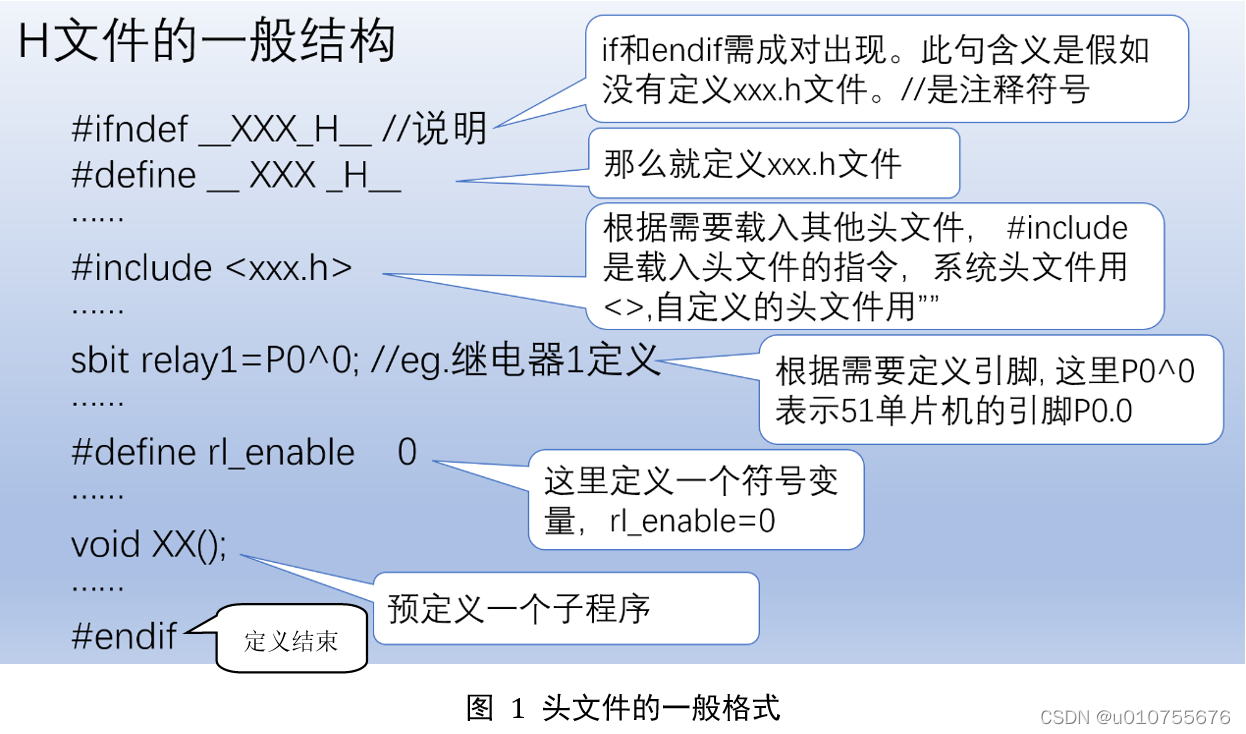
Provided by Chengdu control panel design_ It's detailed_ Introduction to the definition, compilation and quotation of single chip microcomputer program header file
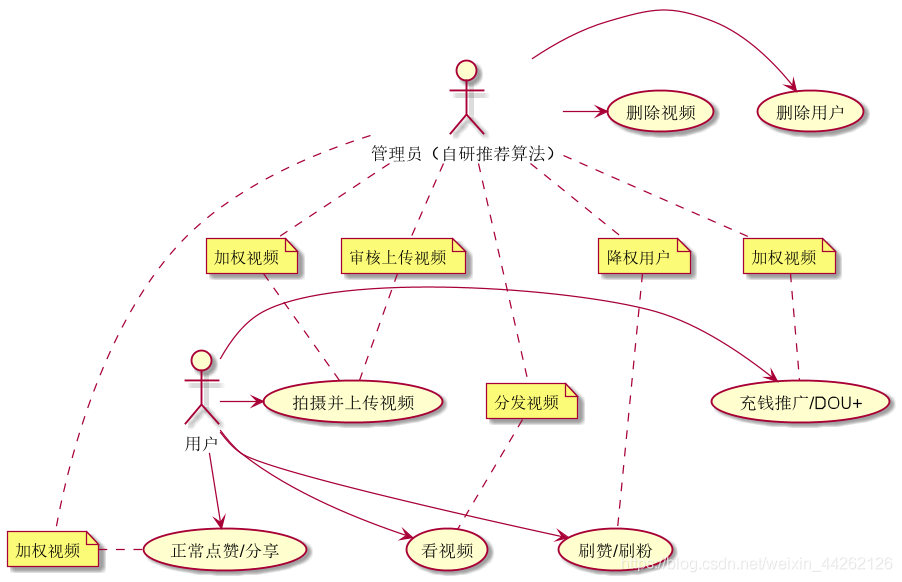
UML project example -- UML diagram description of tiktok

Leetcode exercise - 396 Rotation function
机器学习之逻辑回归(Logistic Regression)原理讲解和实例应用,果断收藏
![[untitled]](/img/6c/df2ebb3e39d1e47b8dd74cfdddbb06.gif)
[untitled]
We reference My97DatePicker to realize the use of time plug-in

ASEMI整流模块MDQ100-16在智能开关电源中的作用
随机推荐
Mds55-16-asemi rectifier module mds55-16
Leetcode162 - find peak - dichotomy - array
Outsourcing for four years, abandoned
3、 Gradient descent solution θ
eolink 如何助力远程办公
Do (local scope), initializer, memory conflict, swift pointer, inout, unsafepointer, unsafebitcast, success
When splicing HQL, the new field does not appear in the construction method
Progress in the treatment of depression
Want to be an architect? Tamping the foundation is the most important
Detailed comparison between asemi three-phase rectifier bridge and single-phase rectifier bridge
ASEMI超快恢复二极管与肖特基二极管可以互换吗
LeetCode149-直线上最多的点数-数学-哈希表
epoll 的 ET,LT工作模式———实例程序
【Proteus仿真】自动量程(范围<10V)切换数字电压表
LeetCode165-比较版本号-双指针-字符串
成都控制板设计提供_算是详细了_单片机程序头文件的定义、编写及引用介绍
SVN详细使用教程
How do I open the win10 startup folder?
Borui data and F5 jointly build the full data chain DNA of financial technology from code to user
Flink DataStream 类型系统 TypeInformation