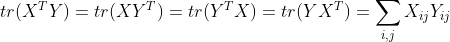正题

题目链接:https://www.luogu.com.cn/problem/CF1286E

题目大意

定义一个字符串$s$的权值为对于每个$s_{L\sim R}=s_{1\sim R-L+1}$的区间，会产生${\min }_{i=L}^R{w}_i$的贡献。

现在开始时$s$为空串，$n$次往$s$后加入一个字符和往$w$序列加入一个数字，然后求这个串的贡献。

强制在线

$1\le n\le 6\times 10^5,1\le w_i<2^{30}$

解题思路

我们在每次加入字符后考虑所有后缀的贡献，然后考虑加入一个字符后后缀产生贡献的变化。

一个想法是对于原来的后缀$[n-len,n-1]$，如果$s_{len+1}=s_n$，那么新的后缀$[n-len,n]$就会产生贡献，否则就不会。除了这些以外还有如果$s_1=s_n$那么后缀$[n,n]$也会产生贡献。

也就是一次操作最多增加一个会产生后缀的贡献，我们取考虑怎么维护其他以前的后缀。

权值方面比较简单，$[n-len,n-1]$的贡献转到$[n-len,n]$的贡献无非就是对$w_i$取$\min$，也就是我们要一个能支持加入删除全部取$min$的数据结构。其实暴力维护都行，我们用map记录贡献为$k$的后缀有多少个，然后每次暴力把大于$w_i$的都修改掉即可，这样势能分析一下就知道是对的。

现在第二个问题是我们怎么知道每次要删除的后缀是哪些。我们建立出KMP的$fail$树，那么原本产生贡献的后缀肯定都在$n-1$点到根节点的路径上，我们维护一个$la{s}_{i,c}$表示节点$i$往祖先走的路上遇到的第一个$x$满足$s_{x+1}=c$的$x$，然后我们就可以一直往上走找到要删除的后缀了。

用$RMQ$维护一下后缀的贡献即可。

时间复杂度：$O(n\log n)$

code

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<map>
#define ll long long
using namespace std;
const ll N=6e5+10,mod=1e18;
ll n,lg[N],nxt[N],las[N][26],ans;
char s[N];map<ll,ll> mp;int f[N][20];
pair<ll,ll> sum;
pair<ll,ll> operator+(const pair<ll,ll> &x,const ll &y)
{
    return make_pair((x.first+y)%mod,x.second+(x.first+y)/mod);}
ll operator%(const pair<ll,ll> &x,const ll &p)
{
    return (x.first%p+(x.second%p)*(mod%p)%p)%p;}
void print(pair<ll,ll> x)
{
    
    if(x.second) printf("%lld%018lld\n",x.second,x.first);
    else printf("%lld\n",x.first);
}
ll Ask(ll l,ll r){
    
	ll z=lg[r-l+1];
	return min(f[r][z],f[l+(1<<z)-1][z]);
}
signed main()
{
    
	scanf("%lld",&n);
	for(ll i=2;i<=n;i++)lg[i]=lg[i>>1]+1;
	ll mask=(1ll<<30),z=0;
	char op[2];ll w=0;
	scanf("%s%lld",op,&w);
	mp[w]++;ans=sum.first=w;
	s[1]=op[0];f[1][0]=w;
	printf("%lld\n",ans);
	for(ll p=2;p<=n;p++){
    
		scanf("%s%lld",op,&w);
		char c=op[0];
		c=(c-97+sum%26)%26+97;s[p]=c;
		w=w^(sum%mask);f[p][0]=w;
		for(ll i=1;(1<<i)<=p;i++)
			f[p][i]=min(f[p][i-1],f[p-(1<<i-1)][i-1]);
		while(z&&s[z+1]!=s[p])z=nxt[z];
		nxt[p]=(z+=(s[z+1]==s[p]));
		for(ll j=0;j<26;j++)las[p][j]=las[nxt[p]][j];
		las[p][s[nxt[p]+1]-'a']=nxt[p];
		for(ll j=0;j<26;j++){
    
			if(j+'a'==c)continue;
			for(ll x=las[p-1][j];x;x=las[x][j]){
    
				ll val=Ask(p-x,p-1);
				mp[val]--;ans=ans+(-val);
			}
		}
		while(mp.size()){
    
			map<ll,ll>::iterator it=mp.end();it--;
			pair<ll,ll> x=*it;
			if(x.first>w){
    
				ans=ans+(-(x.first-w)*x.second);
				mp[w]+=x.second;mp.erase(it);
			}
			else break;
		}
		if(s[p]==s[1])mp[w]++,ans=ans+w;
		sum=sum+ans;print(sum);
	}
	return 0;
}