当前位置:网站首页>Q_04_05 使用Qubits
Q_04_05 使用Qubits
2022-08-09 13:02:00 【MOVCat】
使用Qubits
现在已经看到了Q#语言的各种不同部分,让我们深入了解它,并了解如何使用量子比特本身。
分配Qubits
首先,为了获得我们可以在Q#中使用的量子比特,我们在一个using块中分配量子比特:
using (register = Qubit[5]) {
// Do stuff...
} 以这种方式分配的任何量子位都以 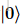 状态开始;在上面的例子中,
状态开始;在上面的例子中, register因此处于状态 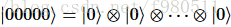
。在using块的末尾,由该块分配的任何量子位将立即解除分配,并且不能继续使用。
警告
目标机器希望在取消分配之前,量子位立即处于 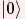 状态,以便它们可以被重用并提供给其他
状态,以便它们可以被重用并提供给其他using块进行分配。尽可能使用单一操作将任何已分配的量子位返回到 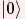 。如果需要, 重置操作可用于测量量子位,并使用该测量结果确保量子位返回到
。如果需要, 重置操作可用于测量量子位,并使用该测量结果确保量子位返回到 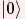
。这样的测量将破坏剩余量子的任何纠缠。
原始门
一旦分配,量子位就可以传递给功能和操作。从某种意义上说,Q#程序可以用qubit来做这些,因为可以采取的行动都被定义为操作。我们将在Primitive Operations和Functions中更详细地看到这些操作,但现在我们提到一些可用于与量子比特交互的有用的基本操作。
首先,单Q位Pauli运算符X,Y和Z在Q#中由原始操作X , Y和Z ,每个(Qubit => () : Adjoint, Controlled)类型为(Qubit => () : Adjoint, Controlled) 。正如原始操作和函数中所描述的那样,我们可以将X看作是一个位翻转操作或NOT门。这让我们可以为  形成一些经典位串s:
形成一些经典位串s:
operation PrepareBitString(bitstring : Bool[], register : Qubit[]) : () {
body {
let nQubits = Length(register);
for (idxQubit in 0..nQubits - 1) {
if (bitstring[idxQubit]) {
X(register[idxQubit]);
}
}
}
adjoint auto
controlled auto
controlled adjoint auto
}
operation Example() : () {
body {
using (register = Qubit[8]) {
PrepareBitString(
[true; true; false; false; true; false; false; true],
register
);
// 此时,register现在具有状态 |11001001〉.
}
}
} Tip
稍后,我们将看到更简洁的书写这种操作的方式,不需要手动流量控制。
我们还可以准备诸如 
来表示的Hadamard变换H
H : (Qubit => () : Adjoint, Controlled) :
operation PreparePlusMinusState(bitstring : Bool[], register : Qubit[]) : () {
body {
// First, get a computational basis state of the form
// |s_0 s_1 ... s_n〉 by using PrepareBitString, above.
PrepareBitString(bitstring, register);
// Next, we use that |+〉 = H|0〉 and |-〉 = H|1〉 to
// prepare the state we want.
for (idxQubit in 0..Length(register) - 1) {
H(register[idxQubit]);
}
}
} 测量
使用Measure操作,这是一个内置的原始门,我们可以从Qubit类型的对象中提取经典信息,并将经典值作为结果赋值,其Result保留为Result ,表示结果不再是量子态。Measure的输入是Bloch球体上的Pauli轴,由Pauli类型的对象(例如PauliX )和类型为Qubit的对象Qubit 。
一个简单的例子是下面的操作,它在 ket0
状态下创建一个量子位,然后对它应用一个Hadamard门H ,然后在PauliZ基础上测量结果。
operation MeasurementOneQubit () : Result {
body {
mutable result = Zero;
// The following using block creates a fresh qubit and initializes it
// in the |0〉 state.
using (qubits = Qubit[1]) {
let qubit = qubits[0];
// We apply a Hadamard operation H to the state, thereby creating the
// state 1/sqrt(2)(|0〉+|1〉).
H(qubit);
// Now we measure the qubit in Z-basis.
set result = M(qubit);
// As the qubit is now in an eigenstate of the measurement operator,
// we reset the qubit before releasing it.
if (result == One) {
X(qubit);
}
}
// Finally, we return the result of the measurement.
return result;
}
} 下面的操作给出了一个稍微复杂的例子,当以指定的泡Qubit[]测量时,返回类型为Qubit[]的寄存器中所有量子位的布尔值为true状态为零,否则为false 。
operation AllMeasurementsZero (qs : Qubit[], pauli : Pauli) : Bool {
body {
mutable value = true;
for (i in 0..Length(qs)-1) {
if ( Measure([pauli], [qs[i]]) == One ) {
set value = false;
}
}
return value;
}
} Q#语言允许经典控制流对量子位测量结果的依赖性。这反过来又能够实现强大的概率小工具,可以降低实施单元的计算成本。举例来说,在Q#中实现所谓的Repeat-Until-Success很容易,这些概率电路在基本门电路方面具有预期的低成本,但真正的成本取决于实际运行和实际交错各种可能的分支。
为了促进Repeat-Until-Success(RUS)模式,Q#支持该构造
repeat {
statement1
}
until (expression)
fixup {
statement2
} 其中statement1和statement2可以是任何有效的Q#语句,并expression任何有效的表达式,其计算结果为Bool类型的值。在一个典型的用例中,下面的电路在Bloch球体上围绕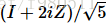
无理轴进行旋转。这是通过使用已知的RUS模式完成的:
operation RUScircuit (qubit : Qubit) : () {
body {
using(ancillas = Qubit[2]) {
ApplyToEachA(H, ancillas);
mutable finished = false;
repeat {
(Controlled X)(ancillas, qubit);
S(qubit);
(Controlled X)(ancillas, qubit);
Z(qubit);
}
until(finished)
fixup {
if AllMeasurementsZero(ancillas, Xpauli) {
set finished = true;
}
}
}
}
} 此示例显示了使用finished的可变变量,该变量位于整个repeat-until-fixup循环的范围内,并在循环之前初始化并在修正步骤中进行更新。
最后,我们给出一个RUS模式的例子来准备量子态 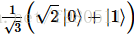 ,从
,从 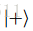 状态开始。另请参阅canon提供的单元测试示例 :
状态开始。另请参阅canon提供的单元测试示例 :
operation RepeatUntilSuccessStatePreparation( target : Qubit ) : () {
body {
using( qubits = Qubit[1] ) {
let ancilla = qubits[0];
H(ancilla);
repeat {
// We expect target and ancilla qubit to be in |+* state.
AssertProb(
[PauliX], [target], Zero, 1.0,
"target qubit should be in the |+* state", 1e-10 );
AssertProb(
[PauliX], [ancilla], Zero, 1.0,
"ancilla qubit should be in the |+* state", 1e-10 );
(Adjoint T)(ancilla);
CNOT(target,ancilla);
T(ancilla);
// The probability of measuring |+* state on ancilla is 3/4.
AssertProb(
[PauliX], [ancilla], Zero, ToDouble(3) / ToDouble(4),
"Error: the probability to measure |+* in the first
ancilla must be 3/4",
1e-10);
// If we get measurement outcome Zero, we prepare the required state
let outcome = Measure([PauliX], [ancilla]);
}
until( outcome == Zero )
fixup {
// Bring ancilla and target back to |+* state
if( outcome == One ) {
Z(ancilla);
X(target);
H(target);
}
}
// Return ancilla back to Zero state
H(ancilla);
}
}
} 此操作中显示的显着编程特性是涉及量子操作的循环的更复杂的fixup部分,以及使用AssertProb语句来确定在程序中某些指定点处测量量子态的概率。另请参阅测试和调试以获取有关Assert和AssertProb语句的更多信息。
边栏推荐
- GIN Bind mode to get parameters and form validation
- FFmpeg multimedia file processing (FFMPEG logging system)
- kustomize entry example and basic syntax instructions
- 快来扔鸡蛋。
- Deep Learning Based on R Language - Simple Regression Case
- Process/Thread related in Sandbox - 1
- ArcEngine(九)图形绘制
- uni-app - uview Swiper 轮播图组件点击跳转链接(点击后拿到 item 行数据, 取出数据做操作)
- The sword refers to Offer 56 - II. Number of occurrences of a number in an array II (bit operation)
- FPGA-近日工作总结
猜你喜欢
随机推荐
Data Mining-06
FPGA - Summary of bugs in ISE (in update)
JS动画函数封装
R language kaggle game data exploration and visualization
handwritten big pile
Realization of RTSP Protocol
telnet+ftp 对设备进行 操控 和 升级
Sandbox中的进程/线程相关-2
puzzle(016.5)逻辑电路
电脑重装系统后桌面图标如何调小尺寸
JS轮播图实现
【瑞吉外卖】day05:增、删、改、查分类以及公共字段自动填充
Oracle Recovery Tools修复空闲坏块
The FPGA - work summary recently
安踏携手华为运动健康共同验证冠军跑鞋 创新引领中国体育
glibc memory management model freeing C library memory cache
jenkins api创建自定义pipeline
阿里大淘系模型治理阶段性分享
Map mixed density function and quantile added line
缓存和数据库一致性问题