当前位置:网站首页>HDU-Tunnel Warfare
HDU-Tunnel Warfare
2022-04-23 06:45:00 【Round moon】
Tunnel Warfare
Title Description
During the War of Resistance Against Japan, tunnel warfare was carried out extensively in the vast areas of north China Plain. Generally speaking, villages connected by tunnels lay in a line. Except the two at the ends, every village was directly connected with two neighboring ones.
Frequently the invaders launched attack on some of the villages and destroyed the parts of tunnels in them. The Eighth Route Army commanders requested the latest connection state of the tunnels and villages. If some villages are severely isolated, restoration of connection must be done immediately!
Input description
The first line of the input contains two positive integers n and m (n, m ≤ 50,000) indicating the number of villages and events. Each of the next m lines describes an event.
There are three different events described in different format shown below:
D x: The x-th village was destroyed.
Q x: The Army commands requested the number of villages that x-th village was directly or indirectly connected with including itself.
R: The village destroyed last was rebuilt.
Output description
Output the answer to each of the Army commanders’ request in order on a separate line.
Sample Input
7 9
D 3
D 6
D 5
Q 4
Q 5
R
Q 4
R
Q 4
Sample Output
1
0
2
4
The main idea of the topic
A list , The selected point is destroyed D. Inquire about Q The length of the continuous interval where the selected point is located .R Restore the last destroyed point .
There is no need to consider repeated destruction
Sample explanation
After three rounds of destruction ,3,6,5 Destroyed .4 The continuous length of position No. is 1

5 Position is destroyed , The length is 0
Restore the last destroyed 5 spot .4 The continuous length of position No. is 2

Restore the last destroyed point 6.4 The continuous length of position No. is 4

Thinking analysis ( Train of thought , Train of thought two )
This problem is solved with two ideas , The first way of thinking , Maintain the maximum and minimum values of the interval to solve . The second way of thinking , The interval merging method of line segment tree is used to solve .
Train of thought
We set the destroyed point to our own id value , If not destroyed, set it to a large number . In this way, we can know that the minimum value from our own point to our rightmost point is our right boundary .

The minimum value found here is 5
If you set the one that hasn't been destroyed to a small value , Then the maximum value from yourself to the leftmost side is your left boundary .

The maximum value found here is 3
Then the middle length is 5-3-1
Special judgment is needed here , If the values of these two values repeat , So that is 0
We set a large value here as length +1, A small value is 0, So we can include the whole interval .
AC Code
//#include<unordered_map>
#include<algorithm>
#include<iostream>
#include<string.h>
#include <iomanip>
#include<stdio.h>
#include<vector>
#include<string>
#include<math.h>
#include<cmath>
#include<queue>
#include<stack>
#include<deque>
#include<map>
#include<set>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const ll ll_inf = 9223372036854775807;
const int int_inf = 2147483647;
const short short_inf = 32767;
const ll less_inf = 0x3f3f3f3f;
const char char_inf = 127;
#pragma GCC optimize(2)
#define accelerate cin.tie(NULL);cout.tie(NULL);ios::sync_with_stdio(false);
#define PI 3.141592653589793
#define EPS 1.0e-8
ll gcd(ll a, ll b) {
return b ? gcd(b, a % b) : a;
}
ll lcm(ll a, ll b) {
return a * b / gcd(a, b);
}
inline ll read() {
ll c = getchar(), Nig = 1, x = 0;
while (!isdigit(c) && c != '-')c = getchar();
if (c == '-')Nig = -1, c = getchar();
while (isdigit(c))x = ((x << 1) + (x << 3)) + (c ^ '0'), c = getchar();
return Nig * x;
}
inline void out(ll a) {
if (a < 0)putchar('-'), a = -a;
if (a > 9)out(a / 10);
putchar(a % 10 + '0');
}
ll qpow(ll x, ll n, ll mod) {
ll res = 1;
while (n > 0) {
if (n & 1)res = (res * x) % mod;
x = (x * x) % mod;
n >>= 1;
}
return res;
}
#define read read()
const int N = 50000;
struct node
{
int maxn, minn;
}tree[N * 4 + 7];
int n, m;
void push_up(int rt)
{
tree[rt].maxn = max(tree[rt << 1].maxn, tree[rt << 1 | 1].maxn);
tree[rt].minn = min(tree[rt << 1].minn, tree[rt << 1 | 1].minn);
}
void creat(int l, int r, int rt)
{
if (l == r)
{
tree[rt].maxn =0;
tree[rt].minn = n+1;
return;
}
int mid = l + r >> 1;
creat(l, mid, rt << 1);
creat(mid + 1, r, rt << 1 | 1);
push_up(rt);
}
void updata(int pos, int maxn, int minn, int l, int r, int rt)
{
if (l == r)
{
tree[rt].maxn = maxn;
tree[rt].minn = minn;
return;
}
int mid = l + r >> 1;
if (pos <= mid)updata(pos, maxn, minn, l, mid, rt << 1);
else updata(pos, maxn, minn, mid + 1, r, rt << 1 | 1);
push_up(rt);
}
node query(int L, int R, int l, int r, int rt)
{
node temp;
int maxn = -int_inf;
int minn = int_inf;
if (L <= l && r <= R)
{
temp.maxn = tree[rt].maxn;
temp.minn = tree[rt].minn;
return temp;
}
int mid = l + r >> 1;
if (L <= mid) {
temp = query(L, R, l, mid, rt << 1);
maxn = max(maxn, temp.maxn);
minn = min(minn, temp.minn);
}
if (R > mid) {
temp = query(L, R, mid + 1, r, rt << 1 | 1);
maxn = max(maxn, temp.maxn);
minn = min(minn, temp.minn);
}
return node{
maxn,minn };
}
stack<int>s;
int main()
{
while (scanf("%d%d", &n, &m) != EOF)
{
while (!s.empty())s.pop();
creat(1, n, 1);
while (m--)
{
char mark[3];
scanf("%s", mark);
if (mark[0] == 'D')
{
int id;
scanf("%d", &id);
updata(id, id, id, 1, n, 1);
s.push(id);
}
else if (mark[0] == 'Q')
{
int id;
scanf("%d", &id);
node left = query(1, id, 1, n, 1);
node right = query(id, n, 1, n, 1);
if (right.minn == left.maxn)puts("0");
else printf("%d\n", right.minn - left.maxn - 1);
}
else
{
int id = s.top();
s.pop();
updata(id, 0, n + 1, 1, n, 1);
}
}
}
}
Train of thought two
We use the method of interval merging , Go to a single point and modify each point . At query time , We judge whether the current point to be searched is located in the combined interval , If it is , When recursing half the interval, you should pay attention to recursing the other half of the interval . See the code for details
AC Code
//#include<unordered_map>
#include<algorithm>
#include<iostream>
#include<string.h>
#include <iomanip>
#include<stdio.h>
#include<vector>
#include<string>
#include<math.h>
#include<cmath>
#include<queue>
#include<stack>
#include<deque>
#include<map>
#include<set>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const ll ll_inf = 9223372036854775807;
const int int_inf = 2147483647;
const short short_inf = 32767;
const ll less_inf = 0x3f3f3f3f;
const char char_inf = 127;
#pragma GCC optimize(2)
#define accelerate cin.tie(NULL);cout.tie(NULL);ios::sync_with_stdio(false);
#define PI 3.141592653589793
#define EPS 1.0e-8
ll gcd(ll a, ll b) {
return b ? gcd(b, a % b) : a;
}
ll lcm(ll a, ll b) {
return a * b / gcd(a, b);
}
inline ll read() {
ll c = getchar(), Nig = 1, x = 0;
while (!isdigit(c) && c != '-')c = getchar();
if (c == '-')Nig = -1, c = getchar();
while (isdigit(c))x = ((x << 1) + (x << 3)) + (c ^ '0'), c = getchar();
return Nig * x;
}
inline void out(ll a) {
if (a < 0)putchar('-'), a = -a;
if (a > 9)out(a / 10);
putchar(a % 10 + '0');
}
ll qpow(ll x, ll n, ll mod) {
ll res = 1;
while (n > 0) {
if (n & 1)res = (res * x) % mod;
x = (x * x) % mod;
n >>= 1;
}
return res;
}
#define read read()
const int N = 50000;
struct node
{
int len, maxn, lmaxn, rmaxn;
}tree[N * 4 + 7];
void push_up(int rt)
{
if (tree[rt << 1].lmaxn == tree[rt << 1].len)
tree[rt].lmaxn = tree[rt << 1].maxn + tree[rt << 1 | 1].lmaxn;
else
tree[rt].lmaxn = tree[rt << 1].lmaxn;
if (tree[rt << 1 | 1].rmaxn == tree[rt << 1 | 1].len)
tree[rt].rmaxn = tree[rt << 1].rmaxn + tree[rt << 1 | 1].maxn;
else
tree[rt].rmaxn = tree[rt << 1 | 1].rmaxn;
tree[rt].maxn = max(tree[rt << 1].rmaxn + tree[rt << 1 | 1].lmaxn, max(tree[rt << 1].maxn, tree[rt << 1 | 1].maxn));
}
void creat(int l, int r, int rt)
{
tree[rt].len = r - l + 1;
if (l == r)
{
tree[rt].rmaxn = tree[rt].lmaxn = tree[rt].maxn = 1;
return;
}
int mid = l + r >> 1;
creat(l, mid, rt << 1);
creat(mid + 1, r, rt << 1 | 1);
push_up(rt);
}
void update(int pos, int mark, int l, int r, int rt)
{
if (l == r)
{
tree[rt].lmaxn = tree[rt].rmaxn = tree[rt].maxn = mark;
return;
}
int mid = l + r >> 1;
if (pos <= mid)update(pos, mark, l, mid, rt << 1);
else update(pos, mark, mid + 1, r, rt << 1 | 1);
push_up(rt);
}
int query(int pos, int l, int r, int rt)
{
int mid = l + r >> 1;
if (l == r || tree[rt].maxn == 0 || tree[rt].maxn == tree[rt].len)
return tree[rt].maxn;
if (pos <= mid)
{
if (pos >= mid - tree[rt << 1].rmaxn + 1)
return query(pos, l, mid, rt << 1) + query(mid + 1, mid + 1, r, rt << 1 | 1);
else
return query(pos, l, mid, rt << 1);
}
else
{
if (pos <= mid + tree[rt << 1 | 1].lmaxn)
return query(mid, l, mid, rt << 1) + query(pos, mid + 1, r, rt << 1 | 1);
else return query(pos, mid + 1, r, rt << 1 | 1);
}
}
stack<int>s;
int main()
{
int n, m;
while (~scanf("%d%d", &n, &m))
{
while (!s.empty())s.pop();
memset(tree, 0, sizeof(tree));
creat(1, n, 1);
while (m--)
{
char Str[5];
scanf("%s", Str);
if (Str[0] == 'D')
{
int id = read;
s.push(id);
update(id, 0, 1, n, 1);
}
else if (Str[0] == 'R')
{
int id = s.top();
s.pop();
update(id, 1, 1, n, 1);
}
else
{
int id = read;
int len = query(id, 1, n, 1);
out(len);
puts("");
}
}
}
}
By-Round Moon
版权声明
本文为[Round moon]所创,转载请带上原文链接,感谢
https://yzsam.com/2022/04/202204230549499640.html
边栏推荐
猜你喜欢
Qt 添加QSerialPort类 实现串口操作
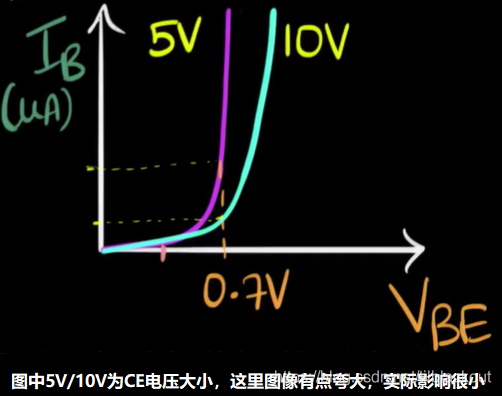
三极管原理及特性分析
Vscode custom comments

OpenCV使用 GenericIndex 进行 KNN 搜索

Collection of practical tips for C language (continuously updated)
VHDL-任意分频器(50%占空比)

深蓝学院激光slam理论与实践 -第二章(里程计标定)作业

QT add qserialport class to realize serial port operation
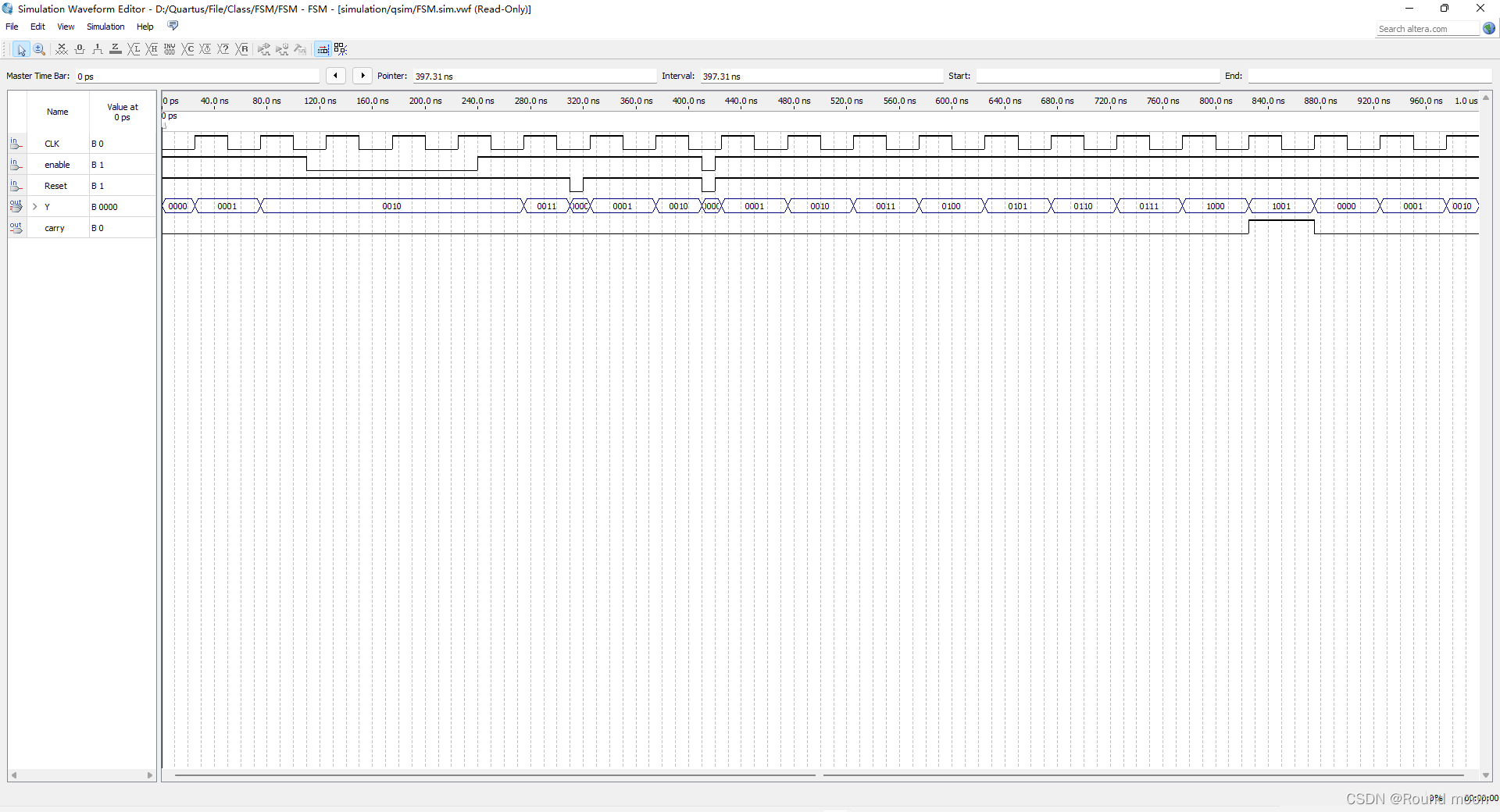
VHDL 有限状态机(FSM) 代码示例
[ThreadX] h743 + ThreadX + Filex migration record
随机推荐
QT add qserialport class to realize serial port operation
Collection of practical tips for C language (continuously updated)
【UDS统一诊断服务】三、应用层协议(2)
Friend function, friend class, class template
Running QT program in visual Stdio
赛氪-二进制
copy constructor
sqlite编译
SQLite compilation
Make your own small program
C#【文件操作篇】PDF文件和图片互相转换
CUDA environment installation
基于SSD的物体检测案例实现
vs中的多字节与unicode
[UDS] unified diagnostic service (UDS)
PN结、二极管原理详解与应用
C语言结构体指定初始化
FOC电机库 定点PID代码分析
C语言进阶要点笔记5
搭建openstack平台

![[ThreadX] h743 + ThreadX + Filex migration record](/img/5b/6796335fd9deeee878cad3e21ab2d9)