当前位置:网站首页>Machine learning - logistic regression
Machine learning - logistic regression
2022-04-23 15:18:00 【Please call me Lei Feng】
One 、 Binomial logistic regression
1. Binomial logistic regression is a function , Final output between 0 To 1 Between the value of the , To solve problems similar to “ Success or failure ”,“ Yes or no " such ” No matter whether or not " The problem of .
2. Logistic regression is a model that maps linear regression model to probability , That is, the output of real number space [-∞,+∞] Mapping to (0,1), So as to obtain the probability .( Personal understanding : The meaning of regression —— The process of making cognition close to truth with observation , Back to the original .)
3. We can intuitively understand this mapping through drawing , We first define a binary linear regression model :
y ^ = θ 1 x 1 + θ 2 x 2 + b i a s , Its in y ^ ∈ ( − ∞ , + ∞ ) \hat{y}=\theta_1x_1+\theta_2x_2+bias, among \hat{y}∈(-∞,+∞) y^=θ1x1+θ2x2+bias, Its in y^∈(−∞,+∞)
Linear regression chart :
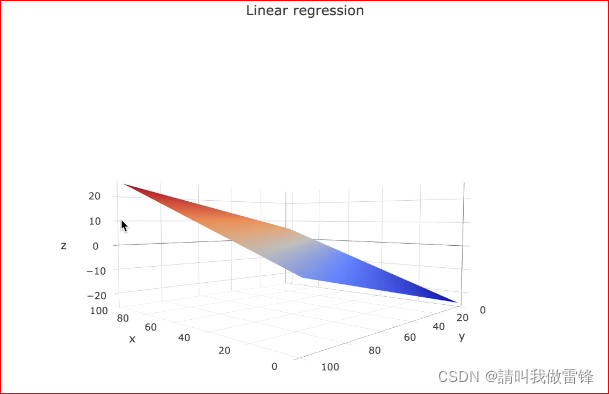
Logistic regression diagram :
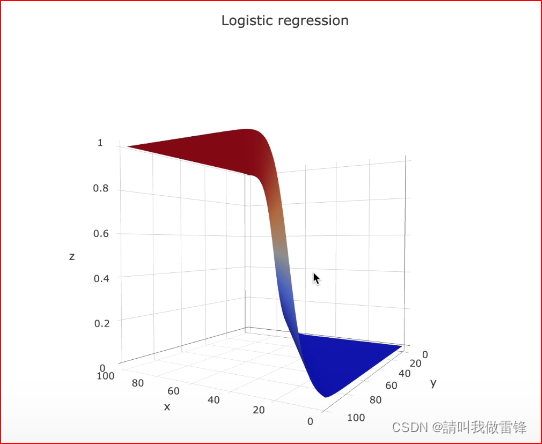
Two 、probability and odds The definition of
1.probability refer to Number of occurrences / The total number of times , Take the coin toss, for example :

p The value range of is [0,+∞)
2.odds Is a ratio , It refers to the possibility of an event ( probability ) And the possibility of not happening ( probability ) The ratio of the . namely Number of occurrences / The number of times it didn't happen , Take the coin toss, for example :

odds The value range of is [0,+∞)
3. Review the Bernoulli distribution : If X Is a random variable in Bernoulli distribution ,X The values for {0,1}, Not 0 namely 1, Such as the front and back of a coin flip :
be :P(X=1)=p,P(X=0)=1-p
Plug in odds:
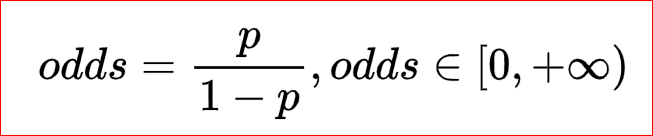
3、 ... and 、logit Functions and sigmoid Functions and their properties :
1.Odds The logarithm of is called Logit, Also writing log-it.
2. We are right. odds take log, Expand odds The value range of is from the space of real numbers [-∞,+∞], This is it. logit function :
l o g i t ( p ) = l o g e ( o d d s ) = l o g e ( p 1 − p ) , p ∈ ( 0 , 1 ) , l o g i t ( p ) ∈ ( − ∞ , + ∞ ) logit(p)=log_e(odds)=log_e(\frac{p}{1-p}),p∈(0,1),logit(p)∈(-∞,+∞) logit(p)=loge(odds)=loge(1−pp),p∈(0,1),logit(p)∈(−∞,+∞)
3. We can use linear regression model to express logit§, Because linear regression model and logit The output function has the same range of values :
for example : l o g i t ( p ) = θ 1 x 1 + θ 2 x 2 + b i a s logit(p)=\theta_1x_1+\theta_2x_2+bias logit(p)=θ1x1+θ2x2+bias
Here are logit§ Function image of , Be careful p∈(0,1), When p=0 perhaps p=1 when ,logit Belongs to undefined .
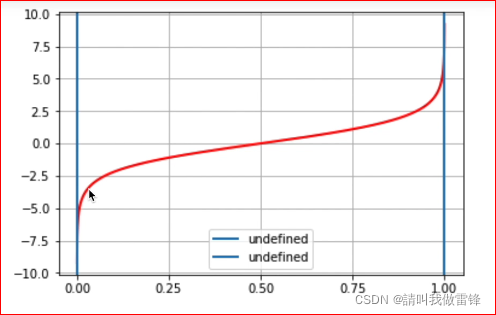
from l o g i t ( p ) = θ 1 x 1 + θ 2 x 2 + b i a s logit(p)=\theta_1x_1+\theta_2x_2+bias logit(p)=θ1x1+θ2x2+bias
have to
l o g ( p 1 − p ) = θ 1 x 1 + θ 2 x 2 + b i a s log(\frac{p}{1-p} )=\theta_1x_1+\theta_2x_2+bias log(1−pp)=θ1x1+θ2x2+bias
notes : Some people may have misunderstandings , Don't understand how to convert ,logit§ Represents the and parameter p Related logarithmic function , ad locum
logit( p )=log(p/(1-p)).
set up z = θ 1 x 1 + θ 2 x 2 + b i a s z=\theta_1x_1+\theta_2x_2+bias z=θ1x1+θ2x2+bias
have to l o g ( p 1 − p ) = z log(\frac{p}{1-p} )=z log(1−pp)=z
Take... On both sides of the equation e The exponential function of the enemy :
p 1 − p = e z \frac{p}{1-p}=e^{z} 1−pp=ez
p = e z ( 1 − p ) = e z − e z p p=e^{z}(1-p)=e^{z}-e^{z}p p=ez(1−p)=ez−ezp
p ( 1 + e z ) = e z p(1+e^z)=e^z p(1+ez)=ez
p = e z ( 1 + e z ) p=\frac{e^z}{(1+e^z)} p=(1+ez)ez
Both numerator and denominator are divided by e z e^z ez, have to
p = 1 ( 1 + e − z ) , p ∈ ( 0 , 1 ) p=\frac{1}{(1+e^{-z})} ,p∈(0,1) p=(1+e−z)1,p∈(0,1)
After the above derivation , We have come to sigmoid function , Finally, the value of the real number space output by the linear regression model is mapped into probability .
s i g m o i d ( z ) = 1 1 + e − z , p ∈ ( 0 , 1 ) sigmoid(z)=\frac{1}{1+e^{-z}} ,p∈(0,1) sigmoid(z)=1+e−z1,p∈(0,1)
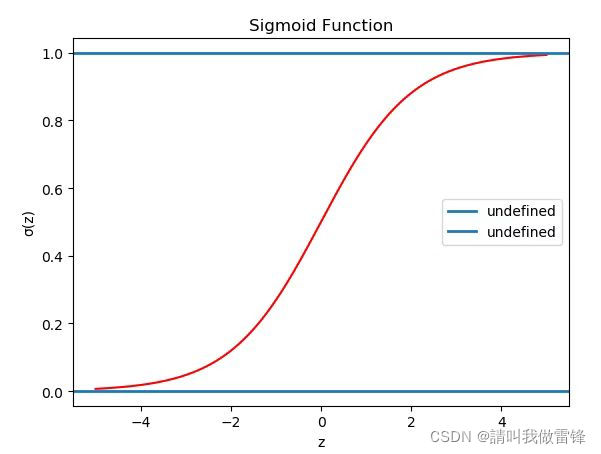
Here is sigmoid Function image of , Be careful sigmoid(z) Value range of
Four 、 Maximum likelihood estimation
1. The assumption function is introduced h θ ( X ) h_\theta(X) hθ(X), set up θ T X \theta^TX θTX It is a linear regression model :
θ T X \theta^TX θTX in , θ T \theta^T θT and X All vectors are columns , for example :
θ T = [ b i a s θ 1 θ 2 ] \theta^T=\begin{bmatrix} bias & \theta_1 &\theta_2 \end{bmatrix} θT=[biasθ1θ2]
X = [ 1 x 1 x 2 ] X=\begin{bmatrix} 1 \\ x_1 \\ x_2 \end{bmatrix} X=⎣⎡1x1x2⎦⎤
Find the dot product of the matrix , obtain :
θ T X = b i a s ∗ 1 + θ 1 ∗ x 1 + θ 2 ∗ x 2 = θ 1 x 1 + θ 2 ∗ x 2 + b i a s \theta^TX=bias*1+\theta_1*x_1+\theta_2*x_2=\theta_1x_1+\theta_2*x_2+bias θTX=bias∗1+θ1∗x1+θ2∗x2=θ1x1+θ2∗x2+bias
set up θ T X = z \theta^TX=z θTX=z, Then there is a hypothetical function :
h θ ( X ) = 1 1 + e − z = P ( Y = 1 ∣ X ; θ ) h_\theta (X)=\frac{1}{1+e^{-z}} =P(Y=1|X;\theta ) hθ(X)=1+e−z1=P(Y=1∣X;θ)
The above expression is under the condition X and θ \theta θ Next Y=1 Probability ;
P ( Y = 1 ∣ X ; θ ) = 1 − h θ ( X ) P(Y=1|X;\theta )=1-h_\theta(X) P(Y=1∣X;θ)=1−hθ(X)
The above expression is under the condition X and θ \theta θ Next Y=1=0 Probability .
2. Review the Bernoulli distribution
f ( k ; p ) { p , i f k = 1 q = 1 − p , i f k = 0 f(k;p)\left\{\begin{matrix} p, &if&k=1 \\ q=1-p, &if&k=0 \end{matrix}\right. f(k;p){
p,q=1−p,ififk=1k=0
perhaps f ( k ; p ) = p k ( 1 − p ) 1 − k f(k;p)=p^k(1-p)^{1-k} f(k;p)=pk(1−p)1−k,for k∈{0,1}. Be careful f(k;p) It means k by 0 or 1 Probability , That is to say P(k)
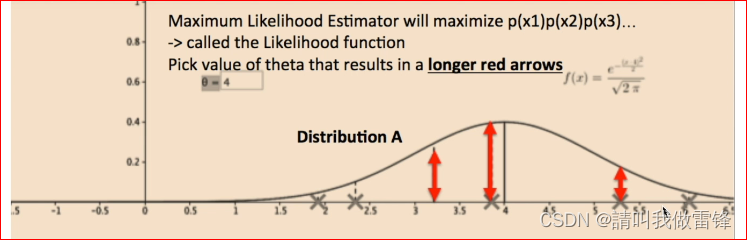
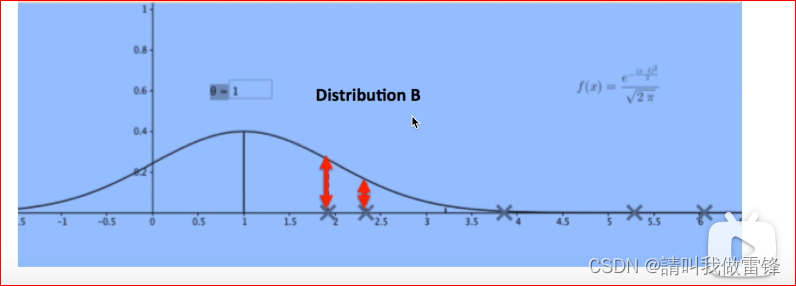
3. The purpose of maximum likelihood estimation is to find a probability distribution that best matches the data .
For example XX Refers to data points , The product of the lengths of all the red arrows in the figure is the output of the likelihood function , obviously , The distribution likelihood function of the upper graph is larger than that of the lower graph , So the distribution of the upper graph is more consistent with the data , Maximum likelihood estimation is to find a distribution that best matches the current data .
4. Define the likelihood function
L ( θ ∣ x ) = P ( Y ∣ X ; θ ) = ∏ i m P ( y i ∣ x i ; θ ) = ∏ i m h θ ( x i ) y i ( 1 − h θ ( x i ) ) ( 1 − y i ) L(\theta|x)=P(Y|X;\theta )=\prod_{i}^{m} P(y_i|x_i;\theta )=\prod_{i}^{m} h_\theta(x_i)^{y_i}(1-h_\theta(x_i))^{(1-{y_i})} L(θ∣x)=P(Y∣X;θ)=i∏mP(yi∣xi;θ)=i∏mhθ(xi)yi(1−hθ(xi))(1−yi),
among i For each data sample , share m Data samples , The purpose of maximum likelihood estimation is to make the above formula “ From output value ” As big as possible ; Top-down extraction log, To facilitate calculation , because log You can convert a product into an addition , And it doesn't affect our optimization goal :
L ( θ ∣ x ) = l o g ( P ( Y ∣ X ; θ ) ) = ∑ i = 1 m y i l o g ( h θ ( x i ) ) + ( 1 − y i ) l o g ( 1 − h θ ( x i ) ) L(\theta|x)=log(P(Y|X;\theta ))=\sum_{i=1}^{m} y_ilog(h_\theta (x_i))+(1-y_i)log(1-h_\theta (x_i)) L(θ∣x)=log(P(Y∣X;θ))=i=1∑myilog(hθ(xi))+(1−yi)log(1−hθ(xi))
We just need to add a minus sign in front of the formula , Then the maximum can be transformed into the minimum , set up h θ ( X ) = Y ^ h_\theta (X)=\hat{Y} hθ(X)=Y^, Get the loss function J ( θ ) J(\theta) J(θ), We just minimize this function , We can get what we want by deriving θ \theta θ:
J ( θ ) = − ∑ i m Y l o g ( Y ^ ) − ( 1 − Y ) l o g ( 1 − Y ^ ) J(\theta)=-\sum_{i}^{m} Ylog(\hat{Y})-(1-Y)log(1-\hat{Y}) J(θ)=−i∑mYlog(Y^)−(1−Y)log(1−Y^)
版权声明
本文为[Please call me Lei Feng]所创,转载请带上原文链接,感谢
https://yzsam.com/2022/04/202204231508367089.html
边栏推荐
- Differential privacy (background)
- MySQL sync could not find first log file name in binary log index file error
- MySQL InnoDB transaction
- How to design a good API interface?
- Will golang share data with fragment append
- C语言超全学习路线(收藏让你少走弯路)
- Detailed explanation of MySQL connection query
- 脏读、不可重复读和幻读介绍
- Little red book timestamp2 (2022 / 04 / 22)
- Five data types of redis
猜你喜欢
Introduction to distributed transaction Seata
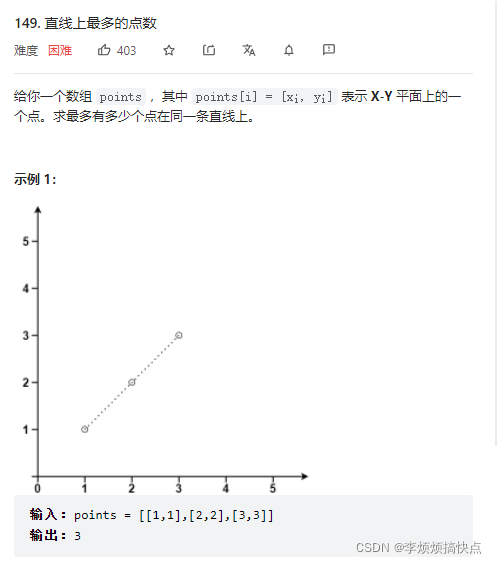
Leetcode149 - maximum number of points on a line - Math - hash table

Leetcode165 compare version number double pointer string

What is the role of the full connection layer?
让阿里P8都为之着迷的分布式核心原理解析到底讲了啥?看完我惊了

LeetCode 练习——396. 旋转函数

Leetcode151 - invert words in string - String - simulation
Tencent has written a few words, Ali has written them all for a month
博睿数据携手F5共同构建金融科技从代码到用户的全数据链DNA

How to design a good API interface?
随机推荐
How to write the keywords in the cover and title? As we media, why is there no video playback
Mysql连接查询详解
Three uses of kprobe
Advanced version of array simulation queue - ring queue (real queuing)
SSH connects to the remote host through the springboard machine
LeetCode153-寻找旋转排序数组中的最小值-数组-二分查找
Share 3 tools, edit 5 works at home and earn more than 400
js——实现点击复制功能
Have you learned the basic operation of circular queue?
Comment eolink facilite le télétravail
MySQL installation process (steps for successful installation)
Borui data and F5 jointly build the full data chain DNA of financial technology from code to user
Share 20 tips for ES6 that should not be missed
MySQL sync could not find first log file name in binary log index file error
JS -- realize click Copy function
Set onedrive or Google drive as a drawing bed in upic for free
Byte interview programming question: the minimum number of K
C语言超全学习路线(收藏让你少走弯路)
async关键字
Hj31 word inversion