题目来源

• leetcode：357. 统计各位数字都不同的数字个数

题目描述

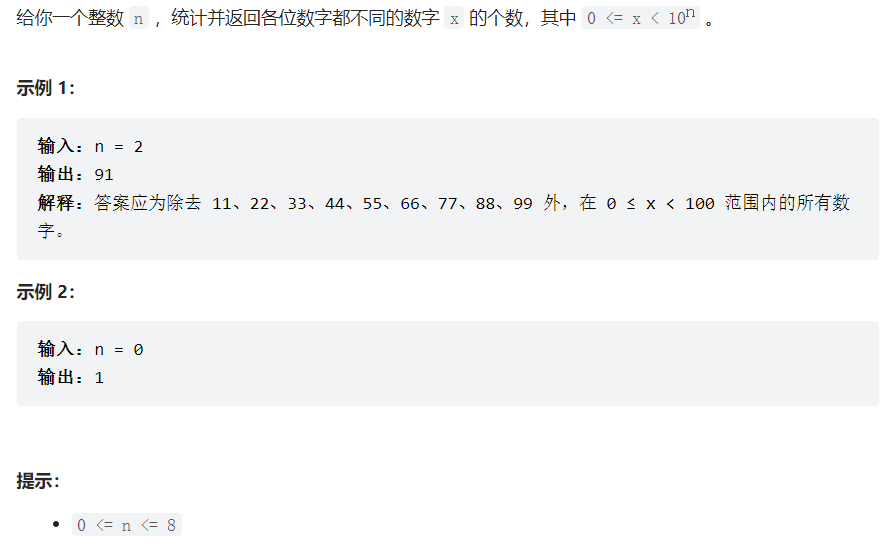
class Solution {
    
public:
    int countNumbersWithUniqueDigits(int n) {
    

    }
};

题目解析

排列组合

思路

首先考虑两种边界情况：

• 当n == 0时， $0<=x<1$，x只有1种选择，即0
• 当n == 1时， $0<=x<10$，x有10种选择，即0 ~ 9（结果为 n == 0 和 n == 1 的和）

当n == 2时， $0<=x<100$，x的选择可以由两部分组成：

• 只有一位数的x：上面已经算过了
• 有两位数的x。由组合数学可得
  • 第一位的选择有9种，即$19$
  • 第二位的选择也有9种，即$09$中除去第一位的选择
• 所以此时一共 9 * 9 + 10 = 91

当n == 3时， $0<=x<1000$，x的选择可以由三部分组成：

• 只有一位数的x：
• 有两位数的x：
• 有三位数的x：
  • 第一位的选择有9种，即$19$
  • 第二位的选择也有9种，即$09$中除去第一位的选择
  • 第三位的选择有8种，即$09$中除去第一位和第二位的选择
• 所以一共有 9 * 9 * 8 + 10

实现

class Solution {
    
public:
    int countNumbersWithUniqueDigits(int n) {
    
        if(n == 0){
    
            return 1;
        }
        if(n == 1){
    
            return 10;
        }
        int ans = 10, curr = 9;
        for (int i = 0; i < n - 1; ++i) {
    
            curr *= (9 - i);
            ans += curr;
        }
        return ans;
    }
};

从上面可以看出，后面的会依赖前面的结论，所以可以用动态规划

动态规划

思路

• n == 0，数字有{0}1个。
• n == 1，数字有{0, 1, 2, 3, 4, 5, 6, 7, 8, 9}10个。
• n == 2，数字包括两部分之和：
  • 一部分为n == 1的所有10个答案
  • 另一部分为长度为2的新增数字
    • 这部分可以在n = 1的所有9个数字的基础上进行拼接（0不能算）。
    • 比如：
      • 从n=1的数字列表{0, 1, 2, 3, 4, 5, 6, 7, 8, 9}中随便取出一个除0以外的数字（因为0不能作为起始数字！，也就是说有9种选择），我们取2好了。
      • 通过在2的尾巴处拼接一位数字可以得到新的合法数字有：{20， 21，23，24，25，26，27，28，29}
      • 可以看到，除了不能在尾巴处拼接一个2（两个连续的2就非法了！），0-9种一共有9个数字可以拿来拼接在尾巴处。新增答案为9个。
    • 同理，对于n=1数字列表{0, 1, 2, 3, 4, 5, 6, 7, 8, 9}中的其他任意非0数也可以进行拼接操作，一共可以新增9*9个答案。
  • 最终，n=2的合法数字，n=1时的答案 + 长度为2的数字个数（9*9个）= 10 + 81 = 91。
• n == 3时同理，只不过此时可以用拼接的数字减少为了8个，此时答案为10 + 9 * 9 + 9 * 9 * 8 = 739。
• 通过归纳不难得到，假设 dp[i] 即 n = i时的答案，则动态转移方程为：dp[i] = dp[i-1] + (dp[i-1] - dp[i-2])*(10-(i-1))
• 转移的初始条件为：dp[0] = 1，dp[1] = 10