当前位置:网站首页>4.1-支持向量机
4.1-支持向量机
2022-08-11 06:50:00 【一条大蟒蛇6666】
文章目录
上一章的二分类问题
- 由于原来右图中黄色的loss函数是无法做梯度下降的,因此我们对它做一个近似(Approximation),用 l l l 来取代 δ δ δ ,此时的 l l l 可以采用很多不同的函数,比如:方差,Sigmoid+方差,Sigmoid+交叉熵(Cross entropy),铰链损失(Hinge loss)


- 当数据中有离群点(Outlier)时,铰链损失(Hinge loss)往往要比交叉熵(Cross entropy)表现得更好
一、铰链损失(Hinge loss)
- 根据下图的推导过程,SVM的loss函数可以通过梯度下降来求解,最后并将SVM转换成了教科书里常见的表达形式。

二、核方法(Kernel Method)
- 对偶表示(Dual Representation):在SVM中, α n ∗ \alpha_n^* αn∗可能是稀疏的,意味着存在一些 α n ∗ = 0 \alpha_n^*=0 αn∗=0的xn,而那些 α n ∗ ≠ 0 \alpha_n^*\neq 0 αn∗=0的xn就是支持向量(support vector)。这些不是0的点最终决定着我们整个模型的好坏,这也是为什么数据中的一些离群点难以对SVM造成影响的原因。
- 核函数(Kernel Fountion):右图中 K ( x n , x ) K(x^n,x) K(xn,x)就是核函数,也就是做 x n 和 x x^n和x xn和x的内积(inner product)

- 核方法(Kernel Trick):当我们的loss函数可以写成左图蓝线那样时,我们就只需要计算 K ( x n ′ , x n ) K(x^{n'},x^n) K(xn′,xn),而并不需要知道向量x的具体值。这就是核方法带来的好处,他不仅可以应用在SVM上,还可以应用在线性回归和逻辑回归上。
- 在右图的推导中我们可以看到x与z做特征变换后再内积是十分复杂的,当我们用核方法后就不需要这么做,直接对x,z进行内积后平方即可。

2.1 径向基函数核(Radial Basis Function Kernel)
- 当x与z越像时,其Kernel值就越大。如果x=z,值为1;x与z完全不一样时,值为0。
- 根据下图的公式推导很容易看出来RBF Kernel是在无穷多维的平面上去做事情,因此模型的复杂度会非常高,这样是非常容易过拟合的。

2.2 Sigmoid Kernel
- 左图中做Sigmoid Kernel时,只有一个隐藏层网络,并且每一个神经元的权重就是一笔数据,神经元的个数就是支持向量的数目。
- 右图中解释了如何直接设计一个核函数K(x,z)来代替Φ(x)和Φ(z),以及通过Mercer’s theory来检验这个核函数是否符合要求。
三、支持向量机相关方法(SVM related methods)
SVR(支持向量回归):当预测值和真实值的差距在某一个范围内时,loss=0
Ranking SVM:当要考虑的东西是一个排序的list时
One-class SVM:他希望属于positive的example都是同一个类别,negative的example就散布在其他地方
下图是SVM和深度学习两者之间的相似之处

边栏推荐
猜你喜欢
【LaTex-错误和异常】\verb ended by end of line.原因是因为闭合边界符没有在\verb命令所属行中出现;\verb命令的正确和错误用法、verbatim环境的用法
Resolved EROR 1064 (42000): You have an error in. your SOL syntax. check the manual that corresponds to yo
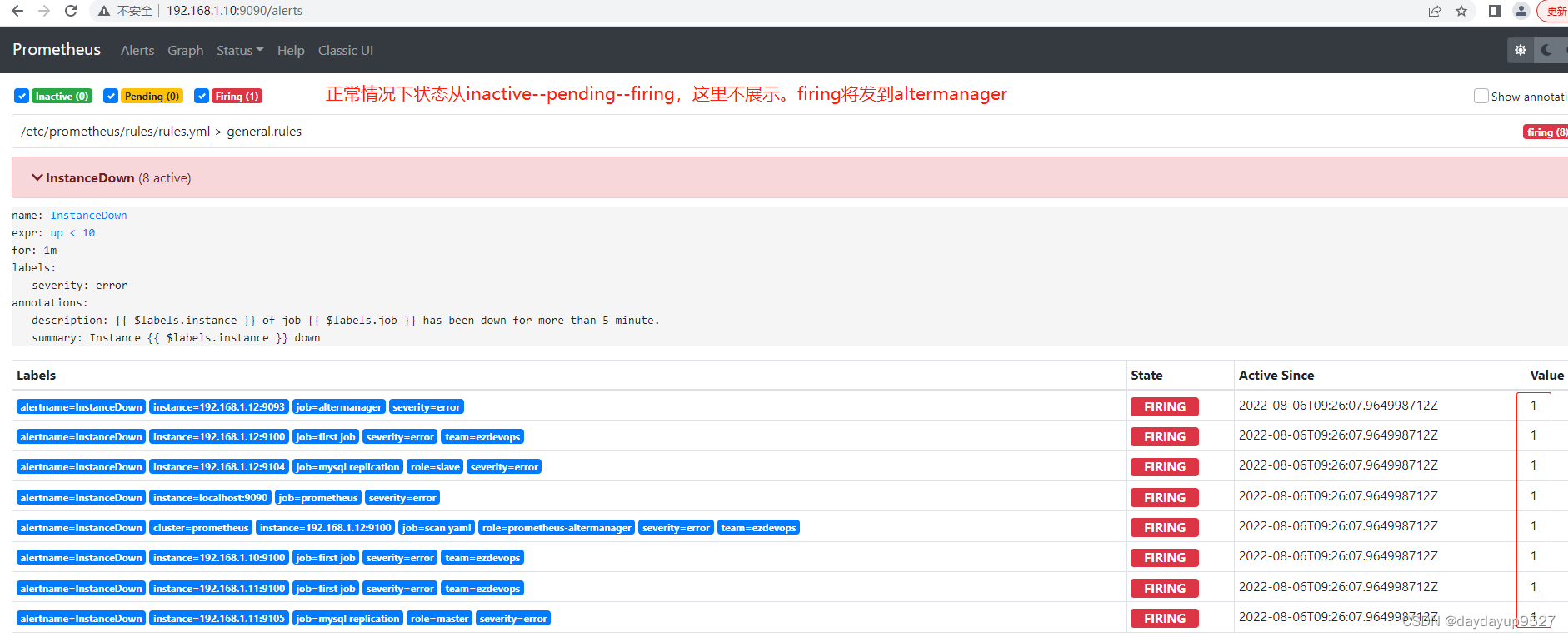
prometheus学习5altermanager
Coordinate system in navigation and positioning

结合均线分析k线图的基本知识

daily sql - query for managers and elections with at least 5 subordinates
囍楽云任务源码
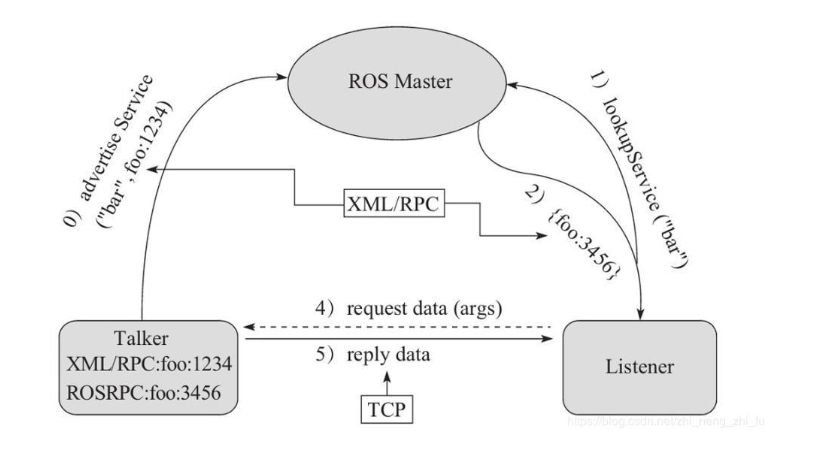
ROS 服务通信理论模型

Daily sql-statistics of the number of professionals (including the number of professionals is 0)

PIXHAWK飞控使用RTK
随机推荐
Unity底层是如何处理C#的
1096 大美数 (15 分)
【深度学习】什么是互信息最大化?
【sdx62】XBL设置共享内存变量,然后内核层获取变量实现
Service的两种启动方式与区别
matplotlib
Redis测试
Internet phone software or consolidation of attack must be "free" calls security clearance
技术分享 | 实战演练接口自动化如何处理 Form 请求?
opencv实现数据增强(图片+标签)平移,翻转,缩放,旋转
结合均线分析k线图的基本知识
深度监督(中继监督)
js判断图片是否存在
基于FPGA的FIR滤波器的实现(5)— 并行结构FIR滤波器的FPGA代码实现
Daily sql-statistics of the number of professionals (including the number of professionals is 0)
Tf中的平方,多次方,开方计算
详述 MIMIC护理人员信息表(十五)
微信小程序功能上新(2022.06.01~2022.08.04)
Edge 提供了标签分组功能
Activity的四种启动模式











