一、估计量的偏置值和方差（Bias and Variance of Estimator）

• 误差（error）的来源：偏置值和方差（Bias and Variance）
• 估计量（Estimator）：我们根据训练集找到的 $f^{\ast }$ 就是真实$\hat{f}$的估计量
• 估计变量x的均值
  • 假设x的均值是u
  • 假设x的方差是${\sigma }^2$
• 估计均值u
  • 取N个点：{ $x^1,x^2,...,x^N$}
  • $m=\frac{1}{N}\sum _n{x}^n\ne u$
  • $E\left[m\right]=E\left[\frac{1}{N}\sum _n{x}^n\right]=\frac{1}{N}\sum _{n}E\left[x^n\right]=u$，虽然每一个m都均匀散布在真实u的四周，但对它们取均值之后就等于u
  • 散布程度：$Var[m]=\frac{{\sigma }^2}{N}$，Var为取m的方差，其值取决于采样的数量。N越大，散布越紧密；N越小，散布越稀疏。
• 估计方差${\sigma }^2$
  • $s^2=\frac{1}{N}\sum _n(x^n-m{)}^2$
  • $E[s^2]=\frac{N-1}{N}{\sigma }^2\ne {\sigma }^2$，N越大，估计量$s^2$与真实方差${\sigma }^2$的差距就越小。

1.1 方差（Variance）

• 越简单的模型，方差越小；越复杂的模型，方差越大
• 简单的模型受数据的影响更小

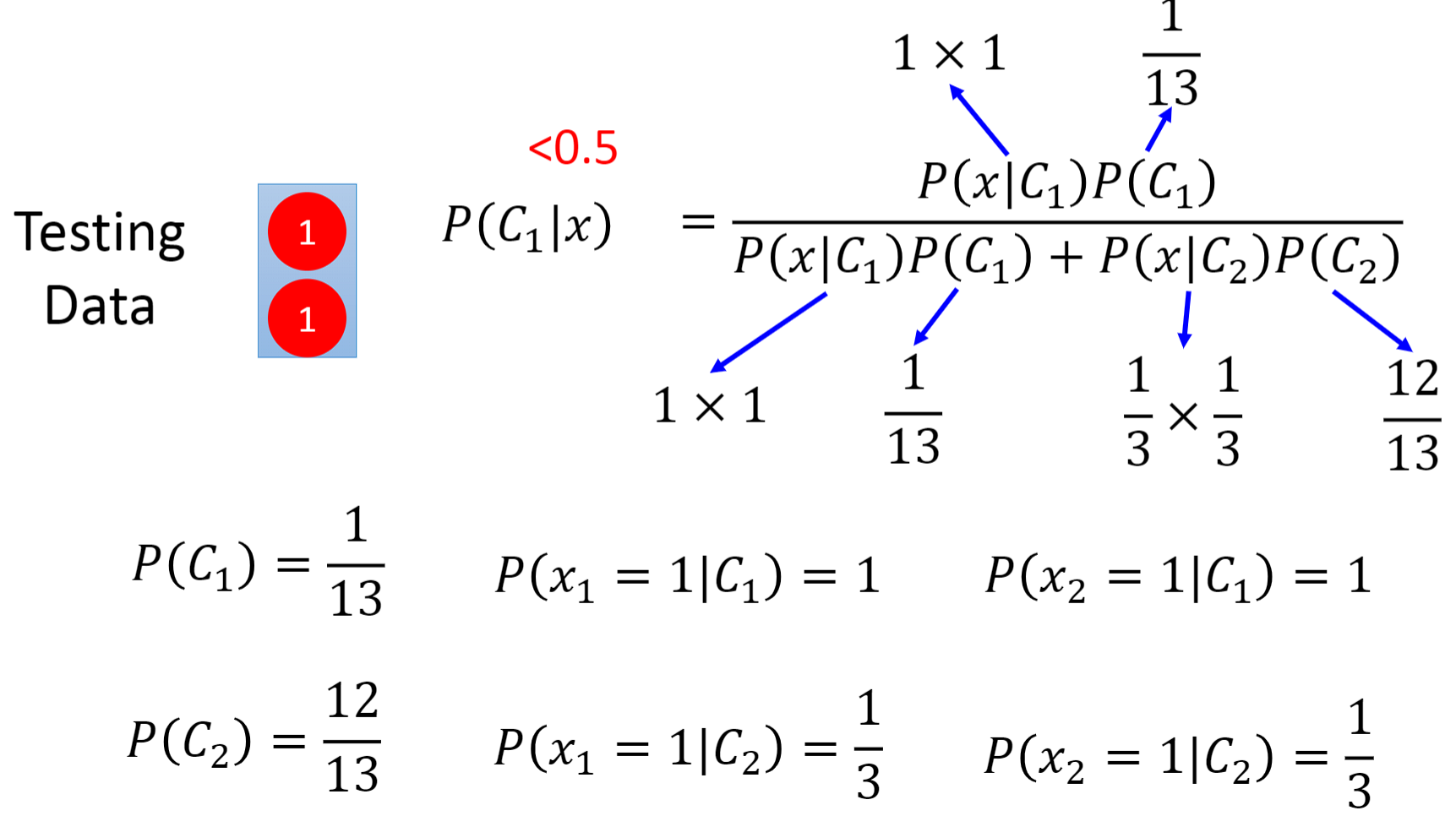
1.3 偏置值（Bias）

• 越简单的模型，偏置值越大；越复杂的模型，偏置值越小
• 对于简单的模型，因为其包含的函数集合范围比较小，可能根本就没有包含真实的函数，因此无论怎么找，也找不出真实的模型。这就是为什么越简单的模型，其偏置值越大的原因。

1.4 模型优化方向

• 当模型的方差（Variance）比较大时，模型就会出现过拟合（Overfitting）。
  • 如果模型在训练集上的拟合效果很好，而在测试集上的效果很差，那么就是方差较大，过拟合
  • 增大数据集：比如采取更多的样本数据，或者对原有数据进行数据增强，这不会改变模型的偏置值（推荐）
    • 手写数字辨识：对训练集的数据进行角度翻转
    • 影像辨识：对训练集的数据进行角度翻转
    • 语音辨识：如果只有男生的数据，没有女生的数据，可以把男生的数据用变声器转换成女生的。如果数据没有杂音干扰，而真实场景又存在杂音干扰。那么可以把该场景的杂音录下来与训练集进行合成，那么就得到了真实场景下的数据。
    • 语音翻译：当手中只有一种国家语言的数据时，却想做10种语言的语音翻译任务，那么可以采取机翻的形式得到多种语言的数据
  • 正则化（Regularization）：在损失函数后面加上一项term，来降低模型对输入的敏感，这样做会缩小模型的空间，也就会增大模型的偏置值。（不推荐）
• 当模型的偏置值（Bias）比较大时，模型就会出现不拟合（Underfitting）。
  • 如果模型在训练集上的拟合效果很差，那么就是偏置值较大，不拟合
  • 此时应该重新设计一下我们的模型，比如增大模型的复杂度：考虑更多的特征，对单个特征考虑多次方

二、交叉验证（Cross Validation）

• 交叉验证
  • 将原始的训练集一分为二，分为真正的训练集和验证集。也就是不要通过公开测试集的结果来优化你的模型，而只是通过验证集的结果来优化你的模型，这样模型就不会出现过拟合，也更能反映你模型的真实情况。
• N次交叉验证（N-fold Cross Validation）
  • 将原始的训练集一分为三，每次取一份数据作为验证集，其他两份做训练集。计算不同模型在以下3种情况下的平均损失值，将表现最好的那一个模型发布到公开测试集上。