当前位置:网站首页>Luogu p1858 [multi person knapsack] (knapsack seeking the top k optimal solution)
Luogu p1858 [multi person knapsack] (knapsack seeking the top k optimal solution)
2022-04-23 04:39:00 【glorious_ dream】

Title Description :
a key : seek 01 In front of the backpack k The value of optimal solution and , And the backpack should be full .
Algorithm analysis :
First ,01 Backpacks should be familiar to everyone , We won't talk about transfer here .
Let's start with the first part : How to keep your backpack full ?
natural 01 The knapsack is from the array with an initial value of 0 Start , That is, every volume will transfer , It is possible to update the answer .
But if you want to fill it up , obviously , Insufficient volume ( No n The volume and energy of an object is this volume ) Obviously not . It seems difficult , But never mind. , We put f The array is first assigned to the minimum value .
What's the advantage of this ? Will find , Because it's painting down layer by layer , So the first layer obviously has only the volume, which is exactly the volume of the first article , The maximum value will be updated ( Because everything else is negative infinity , Will not update ).
Then start painting the second layer , obviously , Only the volume brushed on the first layer , Will then move back ( Because everything else is transferred from negative infinity , It makes no sense , It can't be the maximum ).
Then pay attention to ff The array should have an initial value of 0 ( Later on ).
Let's look at the second part : Seek before k The value of optimal solution and .
set up f[i][j] The volume is i, The first j The value of the optimal solution . At this time , Above said f The initial value of the array can be assigned . hold f[0][1] The assignment is 0, Because the volume is 0 The optimal solution is obviously 0.
We need to consider before k Excellent solution . Start with the optimal solution and look back .
01 Backpack is f[j] and f[j−w[i]]+v[i] The transfer of , Then this question can learn from this idea .
set up x,y The optimal solutions on both sides . If f[j][x]>f[j−w[i]][y], We use an array rnk Before deposit k Excellent solution , At this time rnk[++cnt]=f[j][x], And the x+1. On the contrary, the same is true .
What does this passage mean ? Is to record the capacity of these two backpacks , Which one is big .
Finally, put... Outside f The array has a volume of j Under the condition of k The optimal solution is assigned as rnk An array of former k Just one .
Master code :
#include<bits/stdc++.h>
#define re register
using namespace std;
inline int read(){
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch == '-') f=-1 ; ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48) ; ch=getchar();}
return x*f;
}
inline void print(int x){
if(x/10) print(x/10);
putchar(x%10+'0');
}
const int M = 5010;
int k,value,n,ans;
int w[M],v[M],f[M][60],rnk[M];
signed main(){
k=read(),value=read(),n=read();
for(re int i(1) ; i<=n ; ++i) scanf("%d%d",&w[i],&v[i]);
memset(f,-0x7f7f7f7f,sizeof(f));
f[0][1] = 0;
for(re int i(1) ; i<=n ; ++i){
for(re int j(value) ; j>=w[i] ; --j){
int rn1=1,rn2=1,cnt=0;
while(cnt<=k){
if(f[j][rn1] > f[j-w[i]][rn2]+v[i]){
rnk[++cnt] = f[j][rn1];
rn1++;
}
else{
rnk[++cnt] = f[j-w[i]][rn2]+v[i];
rn2++;
}
}
for(re int h(1) ; h<=k ; ++h) f[j][h] = rnk[h];
}
}
for(re int i(1) ; i<=k ; ++i) ans += f[value][i];
printf("%d",ans);
return 0;
}
版权声明
本文为[glorious_ dream]所创,转载请带上原文链接,感谢
https://yzsam.com/2022/04/202204230402126205.html
边栏推荐
- 【Echart】echart 入門
- Improving 3D object detection with channel wise transformer
- 在AWS控制台创建VPC(无图版)
- leetcode006--查找字符串数组中的最长公共前缀
- eksctl 部署AWS EKS
- 为什么推荐你学嵌入式
- Go反射—Go语言圣经学习笔记
- IDE idea automatic compilation and configuration of on update action and on frame deactivation
- 阿里十年技术专家联合打造“最新”Jetpack Compose项目实战演练(附Demo)
- STM32 upper μ C / shell transplantation and Application
猜你喜欢

Introduction to Cortex-M3 register set, assembly language and C language interface
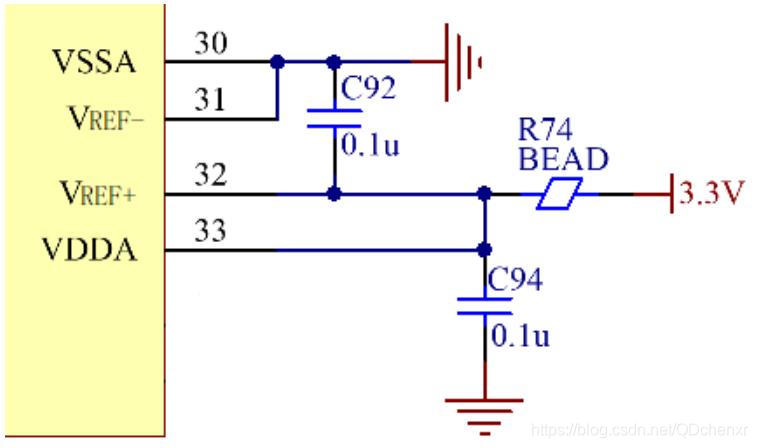
STM32 MCU ADC rule group multi-channel conversion DMA mode
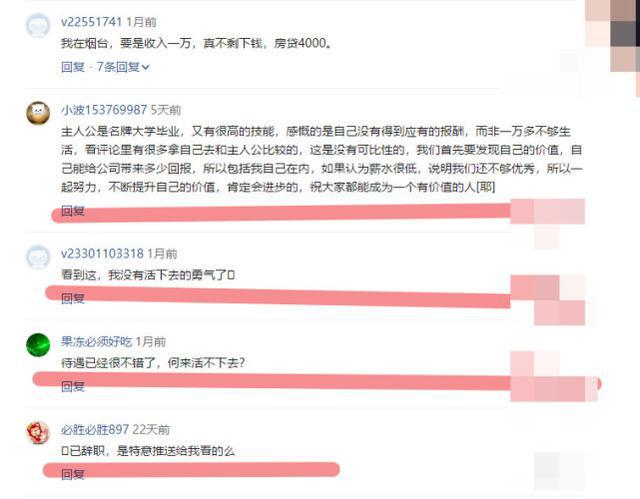
程序员抱怨:1万2的工资我真的活不下去了,网友:我3千咋说
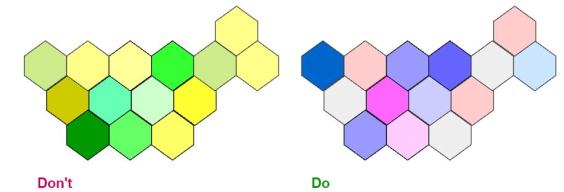
做数据可视化应该避免的8个误区
![[echart] Introduction to echart](/img/40/e057f4ac07754fe6f3500f3dc72293.jpg)
[echart] Introduction to echart
test

win10, mysql-8.0.26-winx64.zip 安装

QML进阶(四)-绘制自定义控件
Go reflection rule

How to regulate intestinal flora? Introduction to common natural substances, probiotics and prebiotics
随机推荐
Coinbase: basic knowledge, facts and statistics about cross chain bridge
leetcode008--实现strStr()函数
Supplement: Annotation
Single chip microcomputer serial port data processing (2) -- ucosiii + cyclic queue receiving data
Redis command Encyclopedia
/etc/bash_completion.d目录作用(用户登录立刻执行该目录下脚本)
Logger and zap log Library in go language
Mysql, binlog log query
Experience summary and sharing of the first prize of 2021 National Mathematical Modeling Competition
数据孤岛是什么?为什么2022年仍然存在数据孤岛?
leetcode003--判断一个整数是否为回文数
MySQL queries users logged in for at least N consecutive days
A new method for evaluating the quality of metagenome assembly - magista
兼容NSR20F30NXT5G的小体积肖特基二极管
Installation and use of Apache bench (AB pressure test tool)
Leetcode->1 两数之和
QML进阶(五)-通过粒子模拟系统实现各种炫酷的特效
Unipolar NRZ code, bipolar NRZ code, 2ASK, 2FSK, 2PSK, 2DPSK and MATLAB simulation
[AI vision · quick review of NLP natural language processing papers today, issue 31] Fri, 15 APR 2022
Introduction to Cortex-M3 register set, assembly language and C language interface