当前位置:网站首页>正交基(线性代数)
正交基(线性代数)
2022-08-10 22:54:00 【xiaozheng123121】
转自:https://blog.csdn.net/u012421852/article/details/80475497
1.正交向量组
直接给定义:欧式空间 V 的一组非零向量,如果他们俩俩向量正交,则称是一个正交向量组。
(1)正交向量组 是 线性无关的,如果向量 a ⃗ ⋅ b ⃗ = 0 \vec{a}\cdot \vec{b}=0 a⋅b=0,则两个向量正交。
(2)n 维欧式空间中俩俩正交的非零向量不会超过 n 个,即 n 维 欧式空间中一个正交向量组最多 n 个向量
2.正交基
在 n 维欧式空间中,由 n 个非零向量组成的正交向量组称为正交基
3.标准正交基
在n维欧式空间中,由 n 个单位向量组成的正交向量组称为标准正交基
比如3维欧式空间中,
(1,0,0)、(0,1,0)、(0,0,1)是一个正交向量组,因为他们俩俩向量正交
(1,0,0)、(0,1,0)、(0,0,1)是一个正交基,因为此正交向量组由n个非零向量组成
(1,0,0)、(0,1,0)、(0,0,1)是一个标准正交基,因为每个向量都是单位向量
参考资料
[1] 正交基 2017.9
边栏推荐
- 【640. Solving Equations】
- 如何利用fiddler连接手机抓包APP
- leetcode:357. 统计各位数字都不同的数字个数
- 手机端出现Z-Fighting现象
- PlaidCTF 2022 Amongst Ourselves:Shipmate writeup
- postman+jmeter接口实例
- 李宏毅机器学习-- Backpropagation
- 【MySQL】mysql因为字符集导致left join出现Using join buffer (Block Nested Loop)
- pytorch tear CNN
- Detailed installation steps and environment configuration of geemap
猜你喜欢

分享一个后台管理系统可拖拽式组件的设计思路
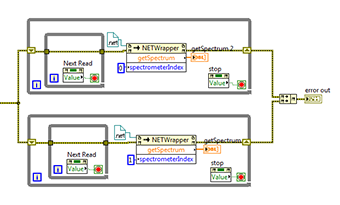
How many threads does LabVIEW allocate?
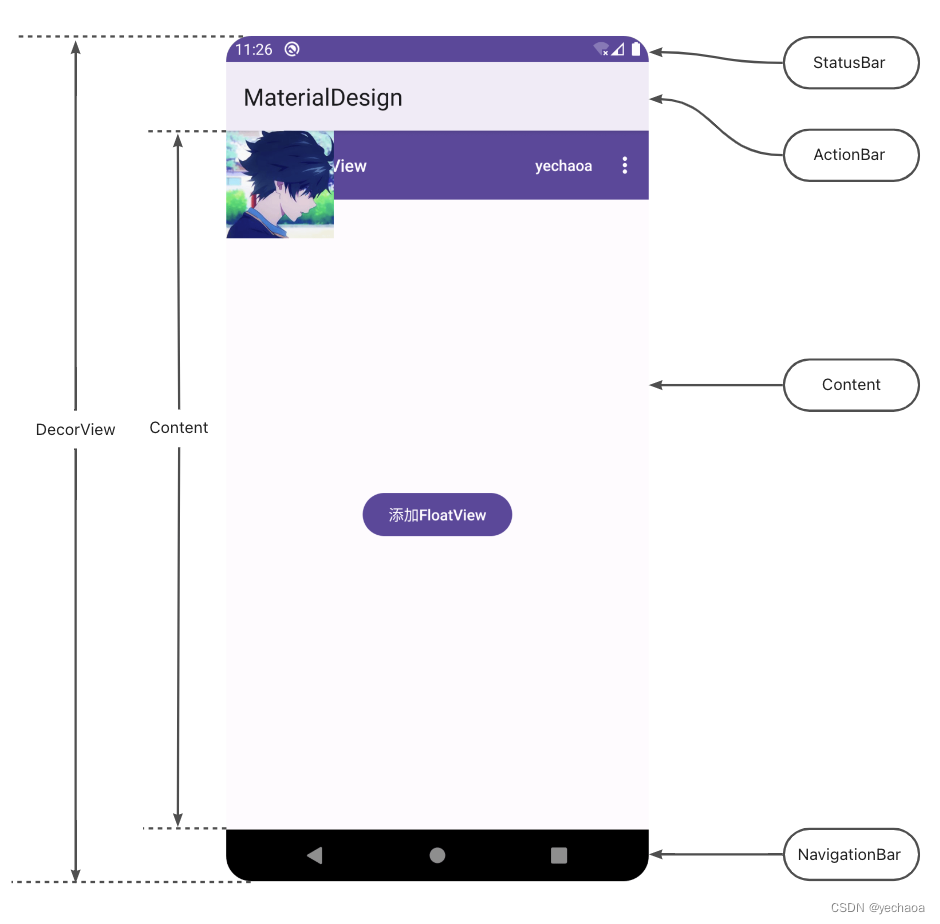
Take you to build a wheel and customize a View that can be dragged and sucked at will

金山云CEO王育林离职:正值冲刺港股之际 雷军曾送金砖
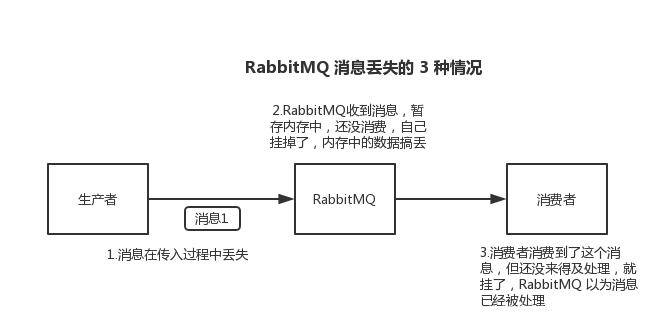
消息队列总结
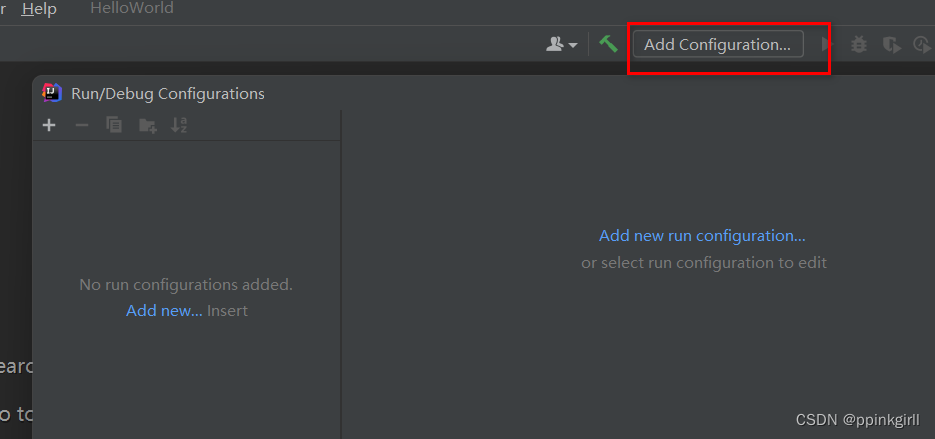
2021IDEA创建web工程
Android | 安卓好用软件来袭,多御安全浏览器免费又强大
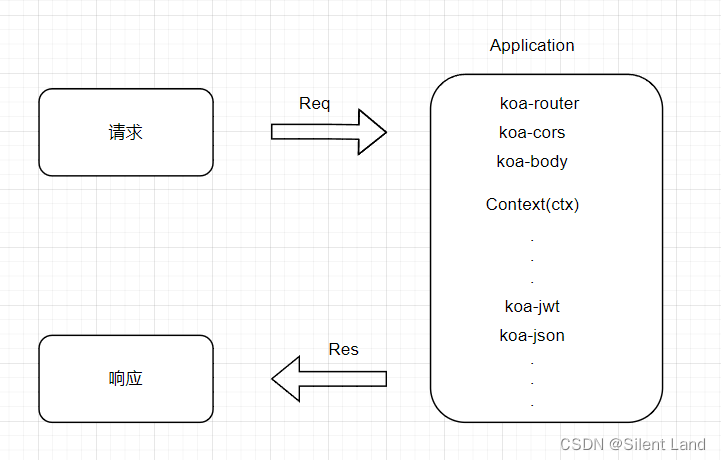
koa框架(一)

信息系统项目管理师核心考点(六十五)信息安全基础知识网络安全

LeetCode Daily 2 Questions 02: Reverse the words in a string (1200 each)
随机推荐
基于深度学习的三维点云分割综述
Pro-test is effective | A method to deal with missing features of risk control data
Redis
响应式pbootcms模板五金配件类网站
【Linux】宝塔面板设置MySQL慢查询日志,未走索引日志
vr虚拟仿真教学系统应用场景开发
带你造轮子,自定义一个随意拖拽可吸边的View
fme csmapreprojector转换器使用高程异常模型进行高程基准转换
使用方便、易于集成、可扩展的用于物流运输行业的文档管理软件
JS use regular expressions in g model and non g difference
二叉树 | 迭代遍历 | leecode刷题笔记
Btree索引和Hash索引
How to be a Righteous Hacker?What should you study?
MySQL之JDBC编程增删改查
瑞幸咖啡第二季营收33亿:门店达7195家 更换CFO
Introduction to the use of counter instructions in Rockwell AB PLC RSLogix5000
Detailed installation steps and environment configuration of geemap
EL表达式
MUI框架开发app中出现的问题
李宏毅机器学习-- Backpropagation