当前位置:网站首页>C - The Battle of Chibi (dp加树状数组前缀和优化)
C - The Battle of Chibi (dp加树状数组前缀和优化)
2022-08-10 02:16:00 【咸蛋_dd】
曹操组成大军,要攻打整个华南。于舟很担心。他认为击败曹操的唯一方法是在曹操的军队中配备一个间谍。但曹操的将领和士兵都是忠诚的,不可能说服他们中的任何一个人背叛曹操。 所以余州只剩下一条路,派人假投降曹操。黄盖被选中执行这一重要任务。不过曹操不太容易相信别人,所以盖煌必须在投降前向曹操泄露一些重要的信息。 于舟和黄盖商量,按照发生的顺序制定了要泄露的NN信息。每个信息估计有一个_{i}a 一世 曹操心目中的价值。 实际上,如果你泄露严格的增值信息,可能会加速让曹操相信你。所以黄盖决定泄露准确的MM信息,严格按照发生顺序递增值。也就是说,黄盖不会改变 NN信息的顺序,只选择其中的MM。 了解黄盖有多少种方法可以做到这一点。
题意:给你一个序列,让你找出里面长度为m的严格递增序列的方案数
思路:首先我想到了dp,设dp[i][j]代表的是到第i个数字,长度为j的方案数。
很容易推出,状态转移方程式为dp[i][j]+=(dp[1][j-1]+dp[2][j-1]+......+dp[i][j-1])
写了朴素做法,很不幸超时了
#include <bits/stdc++.h>
using namespace std;
typedef pair<int,int> PII;
const int N=1010;
const int mod=1e9 +7;
unordered_map<int,int> mp[N];
int a[N];
int main()
{
int t,n,m;
long long int res;
scanf("%d",&t);
for(int z=1;z<=t;z++)
{
res=0;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<i;j++)
{
if(a[i]>a[j])
{
for(int k=1;k<=j;k++)
{
mp[i][k+1]=(mp[i][k+1]+mp[j][k]+1)%mod;
//cout<<mp[i][k+1]<<endl;
}
}
}
}
for(int i=1;i<=n;i++)
{
res+=mp[i][m];
res%=mod;
}
printf("Case #%d: %lld\n",z,res);
for(int i=1;i<=n;i++)
mp[i].clear();
}
}接下来考虑优化,我们会发现,当我们固定dp[i][j]里面的j时(j为严格上升序列的长度),dp[i][j]就可以看作是i从1变化到n的前缀和了,正常暴力的话我们需要n的时间复杂度,这当然是不行的,所以要考虑树状数组优化,我们知道树状数组查询区间和的时间复杂度是O(logn)的,对于这个题刚刚好,所以我们要用树状数组来进行前缀和的优化,这样总体的时间复杂度就是O(n*n*logn)了。
#include <bits/stdc++.h>
using namespace std;
const long long int mod=1e9+7;
const int N=1010;
int c[N],dp[N][N],a[N],b[N];
int n,m;
int lowbit(int x)
{
return x&-x;
}
void add(int x,int y)//插入操作
{
for(;x<=n;x+=lowbit(x))
c[x]=(c[x]+y)%mod;
}
long long int ask(int x)//区间查询
{
long long int sum=0;
for(int i=x;i;i-=lowbit(i))
{
sum=(sum+c[i])%mod;
}
return sum;
}
int main()
{
int t;
scanf("%d",&t);
for(int z=1;z<=t;z++)
{
memset(dp,0,sizeof(dp));
memset(c,0,sizeof(c));
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
b[i]=a[i];
}
sort(b+1,b+1+n);
for(int i=1;i<=n;i++)
{ //这里必须-b+1,因为返回的是一个指针
a[i]=lower_bound(b+1,b+1+n,a[i])-b+1;//lower_bound(x)函数查找序列中第一个大于
//等于x的数,返回下标
}
dp[0][0]=1;
for(int j=1;j<=m;j++)
{
memset(c,0,sizeof(c));
if(j==1) add(1,1);
for(int i=1;i<=n;i++)
{
dp[i][j]=ask(a[i]-1);
add(a[i],dp[i][j-1]);
}
}
long long int ans=0;
for(int i=1;i<=n;i++)
{
ans+=dp[i][m];
ans%=mod;
}
printf("Case #%d: %d\n",z,ans);
}
return 0;
}
边栏推荐
- 【Kali安全渗透测试实践教程】第6章 密码攻击
- 网页挖矿溯源?浏览器浏览历史查看工具Browsinghistoryview
- 【图像分类】2022-CycleMLP ICLR
- Open3D 泊松盘网格采样
- Excel Advanced Drawing Skills 100 Lectures (23) - Countdown Counting in Excel
- SQLserver adds a judgment
- 【QT】QT项目:自制Wireshark
- FusionConpute虚拟机的发放与管理
- [Kali Security Penetration Testing Practice Tutorial] Chapter 6 Password Attack
- 【红队】ATT&CK - 自启动 - 利用LSA身份验证包自启动机制
猜你喜欢
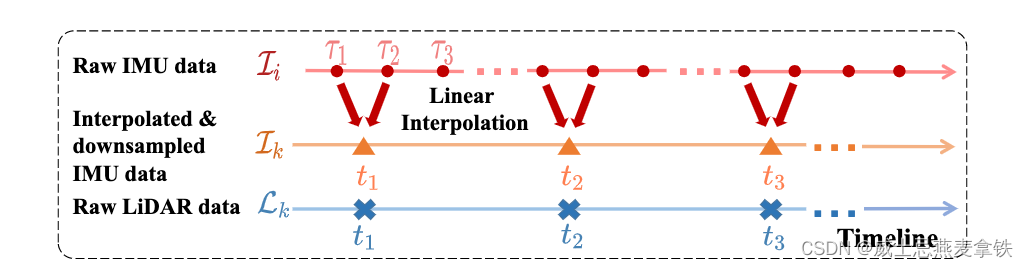
Robust Real-time LiDAR-inertial Initialization (Real-time Robust LiDAR Inertial Initialization) Paper Learning
宝塔服务器PHP+mysql网页URL跳转问题

数据在内存中的存储

数据挖掘和数据仓库之间的区别
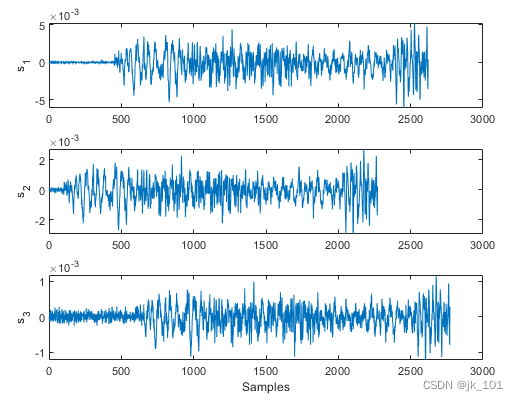
将信号与不同开始时间对齐

【红队】ATT&CK - 自启动 - 利用LSA身份验证包自启动机制
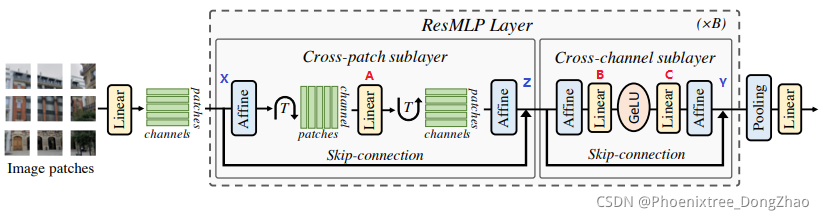
【图像分类】2022-ResMLP

【二叉树-中等】1261. 在受污染的二叉树中查找元素

Deep Learning (5) CNN Convolutional Neural Network
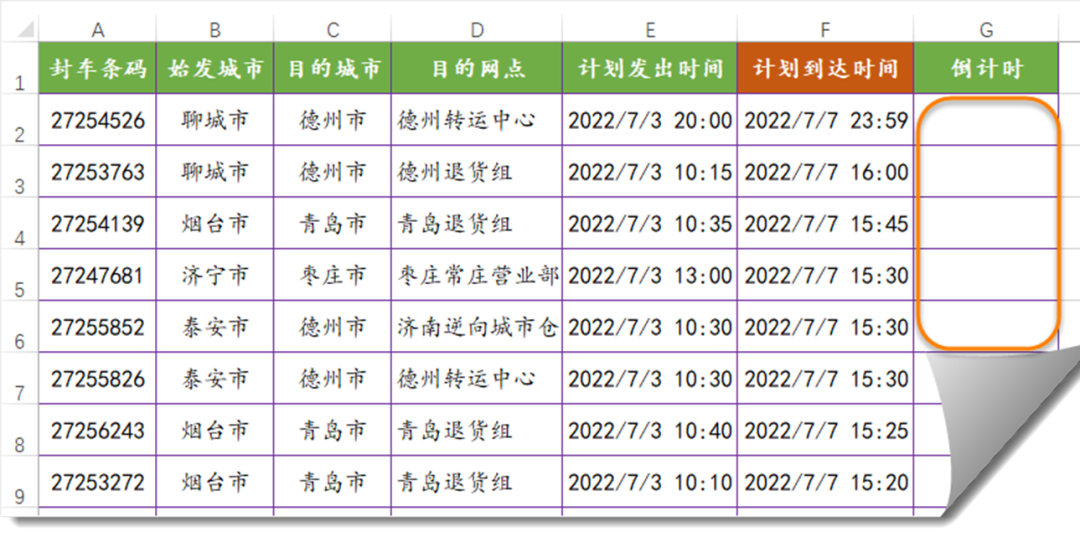
Excel Advanced Drawing Skills 100 Lectures (23) - Countdown Counting in Excel
随机推荐
官宣出自己的博客啦
数据库治理利器:动态读写分离
手把手教你搭建ELK-新手必看-第一章:什么是ELK?
How Microbes Affect Physical Health
2022.8.8 Exam questions for photographer Lao Ma (photographer)
Example 045: Summation
SQLserver加个判断
Deep Learning (5) CNN Convolutional Neural Network
【Kali安全渗透测试实践教程】第9章 无线网络渗透
Open3D 中点细分(网格细分)
HackTheBox——Beep
实例047:函数交换变量
QT模态对话框及非模态对话框学习
781. 森林中的兔子
On the Harvest of Travel
实例048:数字比大小
GDB之指令基础参数
基于C51的中断控制
网页挖矿溯源?浏览器浏览历史查看工具Browsinghistoryview
what is a microcontroller or mcu