当前位置:网站首页>UKFslam
UKFslam
2022-04-23 20:44:00 【xiaoma_ bk】
List of articles
UKF
UKF
- KF Series solution :
Kalman filterNeed a linear modelEKFLinearization by Taylor expansion- A better way to linearize ->
Unscented Transform->UKF- Calculate a set of ( So-called )sigma spot
- From transformation and weighted sigma Point calculation Gauss
Unscented Transform- Calculate a series of Sigma spot
- Every Sigma The point has a weight
- Through nonlinear function transformation Sigma spot
- Weight focus calculation Gauss
Sigma and weight
Sigma spot- choice χ [ i ] {\chi^{[i]}} χ[i], w [ i ] {w^{[i]}} w[i] bring :
- ∑ i w [ i ] = 1 {\sum_i w^{[i]} = 1} ∑iw[i]=1
- μ = ∑ i w [ i ] χ [ i ] { \mu = \sum_i w^{[i]}\chi^{[i]}} μ=∑iw[i]χ[i]
- ∑ = ∑ i w [ i ] ( χ [ i ] − μ ) ( χ [ i ] − μ ) T {\sum = \sum_i w^{[i]}(\chi^{[i]}-\mu)(\chi^{[i]}-\mu)^T} ∑=∑iw[i](χ[i]−μ)(χ[i]−μ)T
- There is no single solution
- How to choose Sigma spot
- first Sigma The point is also the mean χ [ 0 ] = μ {\chi^[0] = \mu} χ[0]=μ
- χ [ i ] = μ + ( ( n + λ ) ∑ ) i {\chi^[i] = \mu + (\sqrt{(n+\lambda)\sum})_i} χ[i]=μ+((n+λ)∑)i for i=1,…,n
- χ [ i ] = μ − ( ( n + λ ) ∑ ) i − n {\chi^[i] = \mu - (\sqrt{(n+\lambda)\sum})_{i-n}} χ[i]=μ−((n+λ)∑)i−n for i=1+n,…,2n
- Square root of matrix
- Definition S S S, ∑ = S S \sum=SS ∑=SS
- By diagonalization :
- ∑ = V D V − 1 = ( d 11 ⋯ 0 ⋮ ⋱ ⋮ 0 ⋯ d n n ) = V ( d 11 ⋯ 0 ⋮ ⋱ ⋮ 0 ⋯ d n n ) ( d 11 ⋯ 0 ⋮ ⋱ ⋮ 0 ⋯ d n n ) V − 1 {\sum=VDV^{-1}= \begin{pmatrix} d_{11} & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & d_{nn} \end{pmatrix} = V\begin{pmatrix} \sqrt{d_{11}} & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & \sqrt{d_{nn}} \end{pmatrix} \begin{pmatrix} \sqrt{d_{11}} & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & \sqrt{d_{nn}} \end{pmatrix} V^{-1}} ∑=VDV−1=⎝⎜⎛d11⋮0⋯⋱⋯0⋮dnn⎠⎟⎞=V⎝⎜⎛d11⋮0⋯⋱⋯0⋮dnn⎠⎟⎞⎝⎜⎛d11⋮0⋯⋱⋯0⋮dnn⎠⎟⎞V−1
- Therefore, we can define : S = V D 1 / 2 V − 1 {S=VD^{1/2}V^{-1}} S=VD1/2V−1
Cholesky MatrixSquare root method- Alternative definition of square root of matrix : L , ∑ = L L T {L, \sum=LL^T} L,∑=LLT
- L , ∑ {L,\sum} L,∑ Have the same eigenvector
- Sigma The point can, but does not have to be located in ∑ {\sum} ∑
- How to set the weight
- w m [ 0 ] = λ n + λ {w_m^{[0]}=\frac{\lambda}{n+\lambda}} wm[0]=n+λλ
- w c [ 0 ] = w m [ 0 ] + ( 1 − α 2 + β ) {w_c^{[0]}=w_m^{[0]}+(1-\alpha^2+\beta)} wc[0]=wm[0]+(1−α2+β)
- w c [ i ] = w m [ i ] + 1 2 ( n + λ ) {w_c^{[i]}=w_m^{[i]}+\frac{1}{2(n+\lambda)}} wc[i]=wm[i]+2(n+λ)1 for i=1,…,2n
- choice χ [ i ] {\chi^{[i]}} χ[i], w [ i ] {w^{[i]}} w[i] bring :
UKF Algorithm
-
Prediction
-
χ t − 1 = ( μ t − 1 , μ t − 1 + ( n + λ ) ∑ t − 1 , μ t − 1 − ( n + λ ) ∑ t − 1 ) {\chi_{t-1}=(\mu_{t-1},\ \ \mu_{t-1}+\sqrt{(n+\lambda)\sum_{t-1}},\ \ \mu_{t-1}-\sqrt{(n+\lambda)\sum_{t-1}})} χt−1=(μt−1, μt−1+(n+λ)∑t−1, μt−1−(n+λ)∑t−1)
-
χ ˉ t ∗ = g ( u t , χ t − 1 ) {\bar{\chi}_t^* = g(u_t,\chi_{t-1})} χˉt∗=g(ut,χt−1)
-
μ t ˉ = ∑ i = 0 2 n w m [ i ] χ ˉ t ∗ [ i ] {\bar{\mu_t}=\sum_{i=0}^{2n}w_m^{[i]}\bar{\chi}_t^{*[i]}} μtˉ=∑i=02nwm[i]χˉt∗[i]
-
Σ ˉ t = ∑ i = 0 2 n w c [ i ] ( χ ˉ t ∗ [ i ] − μ t ˉ ) ( χ ˉ t ∗ [ i ] − μ t ˉ ) T + R t {\bar{\Sigma}_t=\sum_{i=0}^{2n}w_c^{[i]}(\bar{\chi}_t^{*[i]}-\bar{\mu_t})(\bar{\chi}_t^{*[i]}-\bar{\mu_t})^T+R_t} Σˉt=∑i=02nwc[i](χˉt∗[i]−μtˉ)(χˉt∗[i]−μtˉ)T+Rt
-
-
Correction
- χ t ˉ = ( μ t ˉ , μ t ˉ + ( n + λ ) ∑ t − 1 , μ t ˉ − ( n + λ ) ∑ t − 1 ) {\bar{\chi_{t} }=(\bar{\mu_{t}},\ \ \bar{\mu_{t}}+\sqrt{(n+\lambda)\sum_{t-1}},\ \ \bar{\mu_{t}}-\sqrt{(n+\lambda)\sum_{t-1}})} χtˉ=(μtˉ, μtˉ+(n+λ)∑t−1, μtˉ−(n+λ)∑t−1)
- z t ˉ = h ( χ t ˉ ) {\bar{z_t}=h(\bar{\chi_t})} ztˉ=h(χtˉ)
- z t ^ = ∑ i = 0 2 n w m [ i ] z ˉ t [ i ] {\hat{z_t}=\sum_{i=0}^{2n}w_m^{[i]}\bar{z}_t^{[i]}} zt^=∑i=02nwm[i]zˉt[i]
- S t = ∑ i = 0 2 n w c [ i ] ( χ ˉ t [ i ] − μ ˉ t ) ( χ ˉ t [ i ] − μ ˉ t ) T {S_t=\sum_{i=0}^{2n}w_c^{[i]}(\bar{\chi}_t^{[i]}-\bar{\mu}_t)(\bar{\chi}_t^{[i]}-\bar{\mu}_t)^T} St=∑i=02nwc[i](χˉt[i]−μˉt)(χˉt[i]−μˉt)T
- K t = ∑ ˉ t x , z S t − 1 {K_t = \bar{\sum}_t^{x,z}S_t^{-1}} Kt=∑ˉtx,zSt−1
- ∑ t = ∑ ˉ t − K t S t K t T {\sum_t =\bar{\sum}_t - K_tS_tK_t^T} ∑t=∑ˉt−KtStKtT
UT/UKF/EKF Summary
-
UT/UKF
- Unscented Kalman as an alternative to linearization
- UT Is a better approximation than Taylor's expansion
- UT Use sigma Point propagation
- UT Free parameters in
- UKF Use... In the prediction and correction steps UT
-
UKF VS EKF
- The results of the linear model are consistent with EKF identical
- Nonlinear model ratio EKF A better approximation
- The difference is usually “ It's a little small ”
- UKF You don't need a Jacobian determinant
- The same complexity class
- Than EKF Slightly slower
- Still limited by Gaussian distribution
版权声明
本文为[xiaoma_ bk]所创,转载请带上原文链接,感谢
https://yzsam.com/2022/04/202204232041178047.html
边栏推荐
- Unity Odin ProgressBar add value column
- 一. js的深拷贝和浅拷贝
- Leetcode 20. Valid parentheses
- 2022DASCTF Apr X FATE 防疫挑战赛 CRYPTO easy_real
- bounding box iou
- Recognition of high-speed road signs by Matlab using alexnet
- laravel 发送邮件
- 软件测试要怎么学?自学还是培训看完这篇文章你就懂了
- Selenium 显示等待WebDriverWait
- Go zero framework database avoidance Guide
猜你喜欢
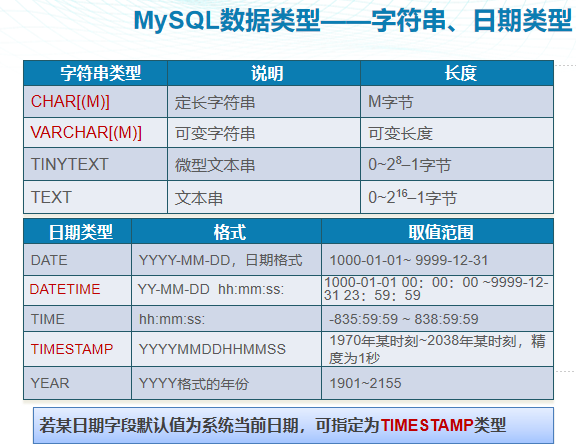
MySQL基础合集
Go language development Daily Fresh Project Day 3 Case - Press Release System II

LeetCode 994、腐烂的橘子
LeetCode 542、01 矩阵
Automatically fill in body temperature and win10 task plan

Case of the third day of go language development fresh every day project - news release system II
Actual measurement of automatic ticket grabbing script of barley network based on selenium (the first part of the new year)
Modeling based on catiav6

居家第二十三天的午饭
上海回应“面粉官网是非法网站”:疏于运维被“黑”,警方已立案
随机推荐
Queue template code
[PTA] l2-011 play with binary tree
Use of node template engine
常用60类图表使用场景、制作工具推荐
How to use PM2 management application? Come in and see
Latest investigation and progress of building intelligence based on sati
三十一. `prototype`显示原型属性和`__proto__`隐式原型属性
2022dasctf APR x fat epidemic prevention challenge crypto easy_ real
Leetcode 709, convert to lowercase
2021-09-02 unity project uses rider to build hot change project failure record of ilruntime
Learn to C language fourth day
Some basic knowledge of devexpress report development
Preliminary understanding of cache elimination algorithm (LRU and LFU)
Create vs project with MATLAB
SQL gets the latest record of the data table
一些接地气的话儿
Three. Based on ply format point cloud voxel model JS upload interface writing
Syntaxerror: unexpected token r in JSON at position 0
Bash script learning -- for loop traversal
上海回應“面粉官網是非法網站”:疏於運維被“黑”,警方已立案