当前位置:网站首页>Snap: 322. Change of Change
Snap: 322. Change of Change
2022-08-10 00:32:00 【empty__barrel】
力扣:322. 零钱兑换
题目:
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额.
计算并返回可以凑成总金额所需的 最少的硬币个数 .如果没有任何一种硬币组合能组成总金额,返回 -1 .
你可以认为每种硬币的数量是无限的.
dp【j】的含义:
dp[j]:凑足总额为j所需钱币的最少个数为dp[j]
递推公式:
dp[j] = min(dp[j - coins[i]] + 1, dp[j]);
初始化:
dp【0】为0的原因:amount是可以等于0的,At the same time, it is logically obviousdp【0】 = 0
因为dp[j]Choose the smaller of the two = min(dp[j], dp[j-coins[i]]+1);所以下标非0的元素都是应该是最大值.
遍历顺序:
This question is completely backpack type,So from childhood to adulthood 遍历,At the same time, the minimum number of coins required is not involved in the sequence,所以本题的两个forNesting of loops is not required,谁先谁后都行.
The reason for setting the judgment condition before the recursive function:
因为dp[j] = min(dp[j], dp[j-coins[i]]+1);If this operationdp[j - coins[i]] == INT_MAX那么dp[j-coins[i]]+1就越界了,So we need to set a judgment condition.
代码:
class Solution {
public:
int coinChange(vector<int>& coins, int amount) {
vector<int>dp(amount+1,INT_MAX);
dp[0] = 0;
for(int i = 0; i < coins.size(); ++i){
for(int j = coins[i]; j <= amount; ++j){
if (dp[j - coins[i]] != INT_MAX) dp[j] = min(dp[j], dp[j-coins[i]]+1);
}
}
if(dp[amount] == INT_MAX) return -1;
return dp[amount];
}
};
边栏推荐
- APS系统能消除造成生产和运输延迟的瓶颈
- 后台管理实现导入导出
- The 2022-8-9 sixth group of input and output streams
- 毕昇编译器优化:Lazy Code Motion
- 【燃】是时候展现真正的实力了!一文看懂2022华为开发者大赛技术亮点
- Bi Sheng Compiler Optimization: Lazy Code Motion
- Sun Zhengyi lost 150 billion: it was expensive at the beginning
- 杭电多校-Counting Stickmen-(思维+组合数+容斥)
- 深度学习100例 —— 循环神经网络(RNN)实现股票预测
- 信息系统项目管理师---第十一章项目风险管理历年考题
猜你喜欢
随机推荐
VR全景拍摄如何拍摄?如何使用拍摄器材?
Leetcode 235. 二叉搜索树的最近公共祖先
What is the stability of the quantitative trading interface system?
高手这样看现货白银走势图
Sun Zhengyi lost 150 billion: it was expensive at the beginning
matplotlib散点图自定义坐标轴(文字坐标轴)
2022-08-09 mysql/stonedb-慢SQL-Q16分析
干涉BGP的选路---社团属性
JS中表单操作、addEventListener事件监听器
学习编程的第十二天
DXF笔记:文字对齐的研究
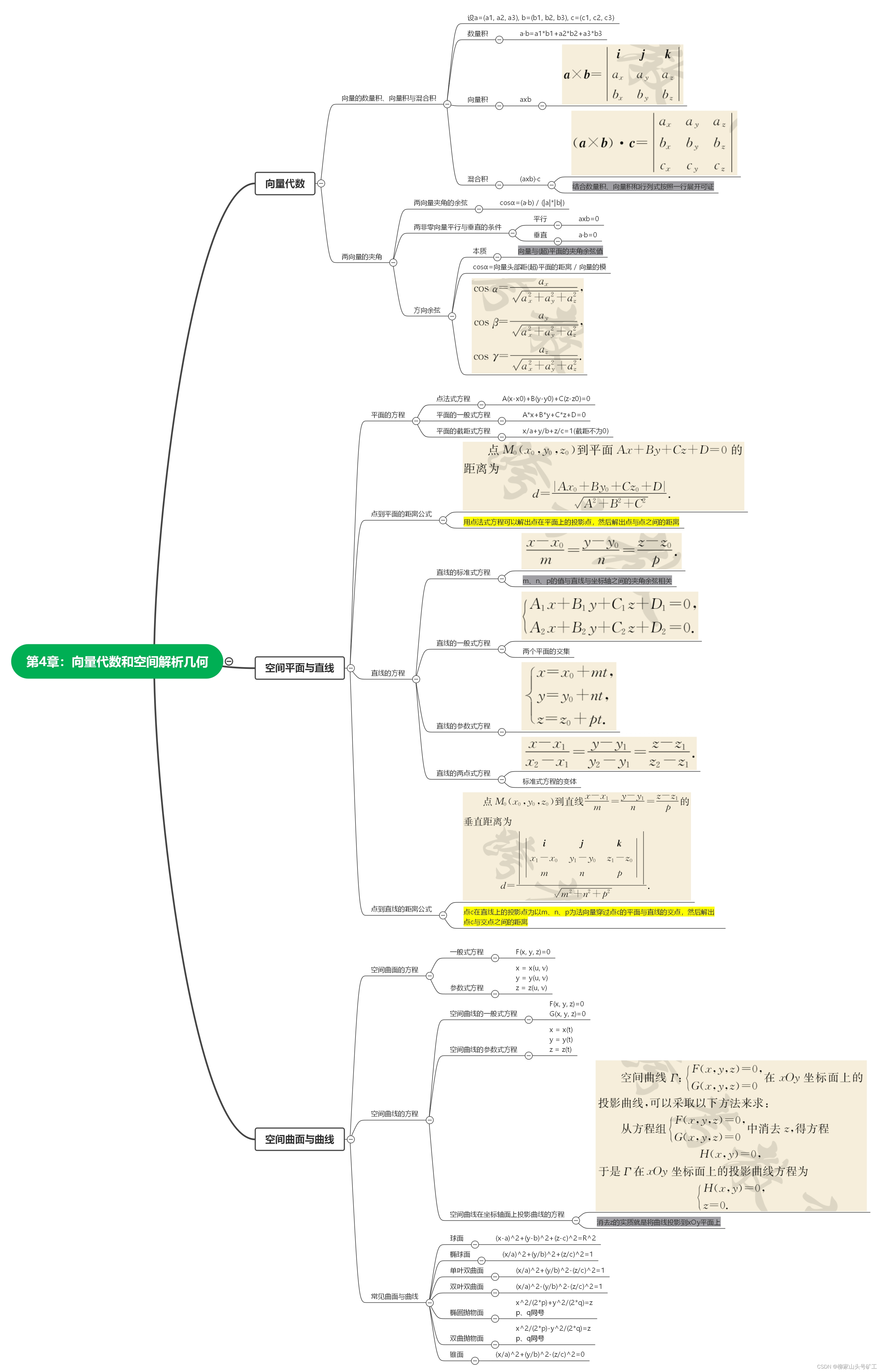
高数_复习_第4章:向量代数和空间解析几何
如何坚持使用程序化系统?
【接口测试】requests 库请求体字符串解码
继承关系下构造方法的访问特点
华为云全流程护航《流浪方舟》破竹首发,打造口碑爆款
JS--hashchange事件--使用/教程
金仓数据库 KingbaseGIS 使用手册(6.3. 几何对象创建函数)
daemon
【TS技术课堂】时间序列预测