当前位置:网站首页>[split of recursive number] n points K, split of limited range
[split of recursive number] n points K, split of limited range
2022-04-23 15:43:00 【MC happy bitter little fear】
I made up the title myself
1.n branch k
Ⅰ:
N Split K term ①
Title Description
Problem description
Yes N Marbles are to be distributed to K personal , Given N、K, Find out how many distribution schemes there are .
Input description
a line , Two integers , by N、K
Output description
An integer , Indicates the number of schemes allocated .
sample input
7 3
sample output
36
Data range
1<=K<=8
K<=N<=30
Tips
4 The ball is divided among three people , Yes 15 There are three kinds of distribution schemes
0 0 4
0 1 3
0 2 2
0 3 1
0 4 0
1 0 3
1 1 2
1 2 1
1 3 0
2 0 2
2 1 1
2 2 0
3 0 1
3 1 0
4 0 0
Be careful :1 3 5, 1 5 3, 3 5 1 Count as 3 Kind of plan
#include <iostream>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <string>
#include <cstring>
#include <vector>
#include <stack>
#include <list>
#include <limits.h>
using namespace std;
int cnt=0;
int n,k;
void doit(int x,int step) //x Is the number of table tennis balls left ,step Who is currently assigned to
{
if(step==k){
// It's time to count , Can't be divided , The “ return ” 了 !
cnt++; // As a plan
return; // Keep looking for solutions qwq
}
for(int i=0;i<=x;i++)doit(x-i,step+1); // From everyone's least 0 Start , List every possible solution , And finally get the answer
}
int main()
{
cin>>n>>k;
doit(n,1);
cout<<cnt;
// Direct results
return 0;
}
Title Description
N A ping-pong ball , Divide into K Pile up , How many different ways of dividing .
for example :n=7,k=3, The following three partition schemes are considered to be the same .
1 1 5
1 5 1
5 1 1
The sample input
7 3
Sample output
4
Tips
6<N<=200
2<=K<=6
The title here clearly states that there can be no such repeated allocation method , So how to allocate n?
This question is actually a recursive Apple , It's just a slight change .
The recursive method ①
int apple(int m,int n){
// Pure recursive thinking
if(m==0||n==1) return 1;
if(n>m) return apple(m,m);
else return apple(m,n-1)+apple(m-n,n);
}
The recursive method ②
void apple(int pre,int n,int step){
// The idea of recursion
if(step==1) {
cnt++;
return;
}
for(int i=pre;i<=n/step;i++)apple(i,n-i,step-1);
}
A limited range of splits ①
Title Description
Problem description
Yes N A pearl is to be distributed to K personal , Everyone is required to be at least MIN star , At most MAX star . Given N、K、MIN、MAX, Find the number of schemes that meet the allocation requirements , If there is no suitable scheme , The output 0.
Input description
a line , Four integers , respectively N、K、MIN、MAX
Output description
An integer , Indicates the number of schemes that meet the allocation requirements .
sample input
7 3 1 4
sample output
12
Data range
K<=N<=30
Data range
1<=K<=8
K<=N<=30
Be careful :1, 3, 5 1, 5, 3 5, 3, 1 Count as 3 Kind of plan
This problem actually limits the boundary between the top and bottom , In fact, we just need to bring the upper and lower boundaries into the problem , It's easy to write
#include <iostream>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <string>
#include <cstring>
#include <vector>
#include <stack>
#include <list>
#include <limits.h>
using namespace std;
int cnt=0,maxn,minn;
int n,k;
void doit(int x,int step)
{
if(step==k){
if(x>=minn && x<=maxn)cnt++; // Judge whether this scheme is legal
return; // Whether it is legal or not, we should continue to find new solutions
}
for(int i=minn;i<=min(maxn,x);i++)doit(x-i,step+1); // If the rest is not enough maxn, Then we can only enumerate x( That is to say min(maxn,x))
}
int main()
{
cin>>n>>k>>minn>>maxn;
doit(n,1);
cout<<cnt;
return 0;
}
A limited range of splits ②
Title Description
Problem description
Yes N A table tennis ball is divided into K Pile up , Each pile is required to be at least MIN individual , At most MAX individual . Given N、K、MIN、MAX, Find the number of schemes that meet the allocation requirements , If there is no suitable scheme , The output 0.
Input description
a line , Four integers , respectively N、K、MIN、MAX
Output description
An integer , Indicates the number of schemes that meet the allocation requirements .
sample input
7 3 1 4
sample output
3
Data range
K<=N<=30
Data range
1<=K<=8
K<=N<=30
Be careful :1, 3, 5 1, 5, 3 5, 3, 1 Count as 1 Kind of plan
Again , On the code :
void doit(int x,int step,int o)
{
if(step==k){
if(x>=max(o,minn) && x<=maxn)cnt++;
return;
}
for(int i=max(o,minn);i<=min(maxn,x);i++)doit(x-i,step+1,i);
}
版权声明
本文为[MC happy bitter little fear]所创,转载请带上原文链接,感谢
https://yzsam.com/2022/04/202204231531525851.html
边栏推荐
- JVM-第2章-类加载子系统(Class Loader Subsystem)
- 建设星际计算网络的愿景
- MySQL Cluster Mode and application scenario
- 腾讯Offer已拿,这99道算法高频面试题别漏了,80%都败在算法上
- One brush 312 - simple repetition set - Sword finger offer 03 Duplicate number in array (E)
- C language --- advanced pointer
- Redis master-slave replication process
- fatal error: torch/extension. h: No such file or directory
- Pgpool II 4.3 Chinese Manual - introductory tutorial
- ICE -- 源码分析
猜你喜欢
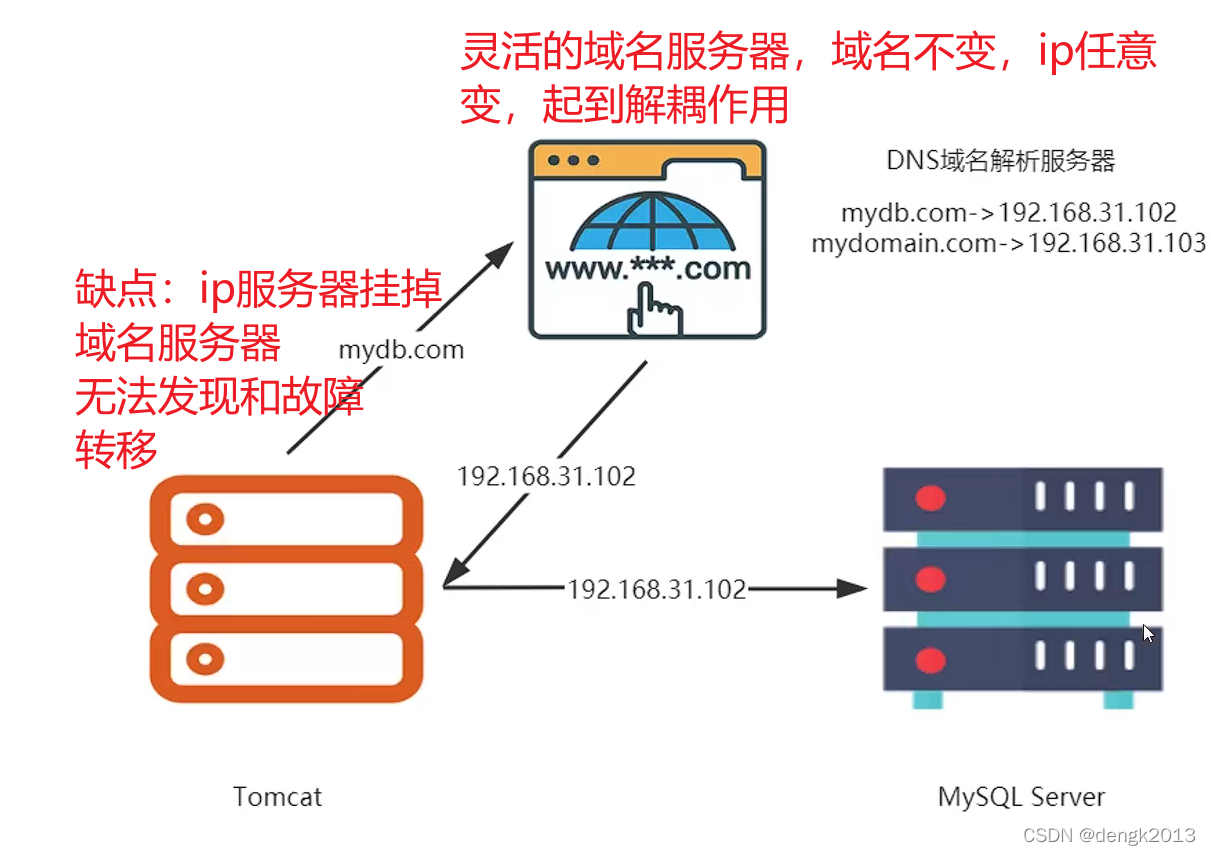
Why is IP direct connection prohibited in large-scale Internet
cadence SPB17. 4 - Active Class and Subclass

Treatment of idempotency
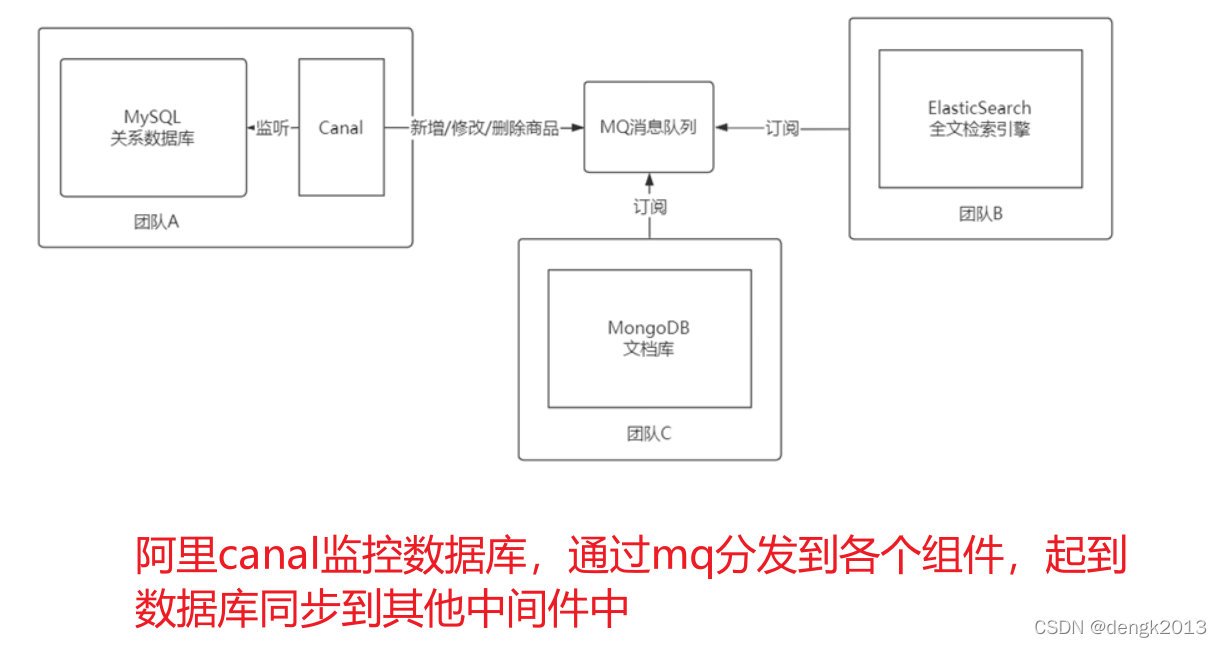
MySQL集群模式與應用場景
服务器中毒了怎么办?服务器怎么防止病毒入侵?
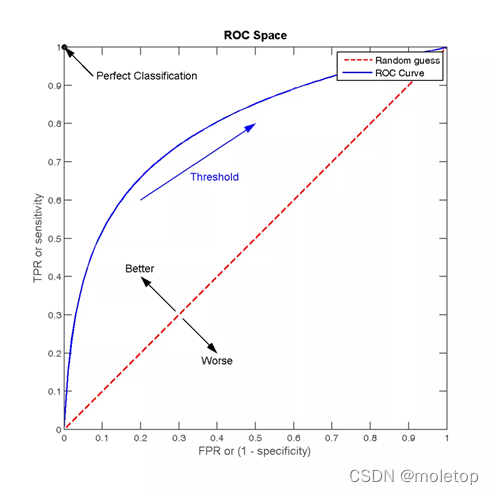
Recommended search common evaluation indicators
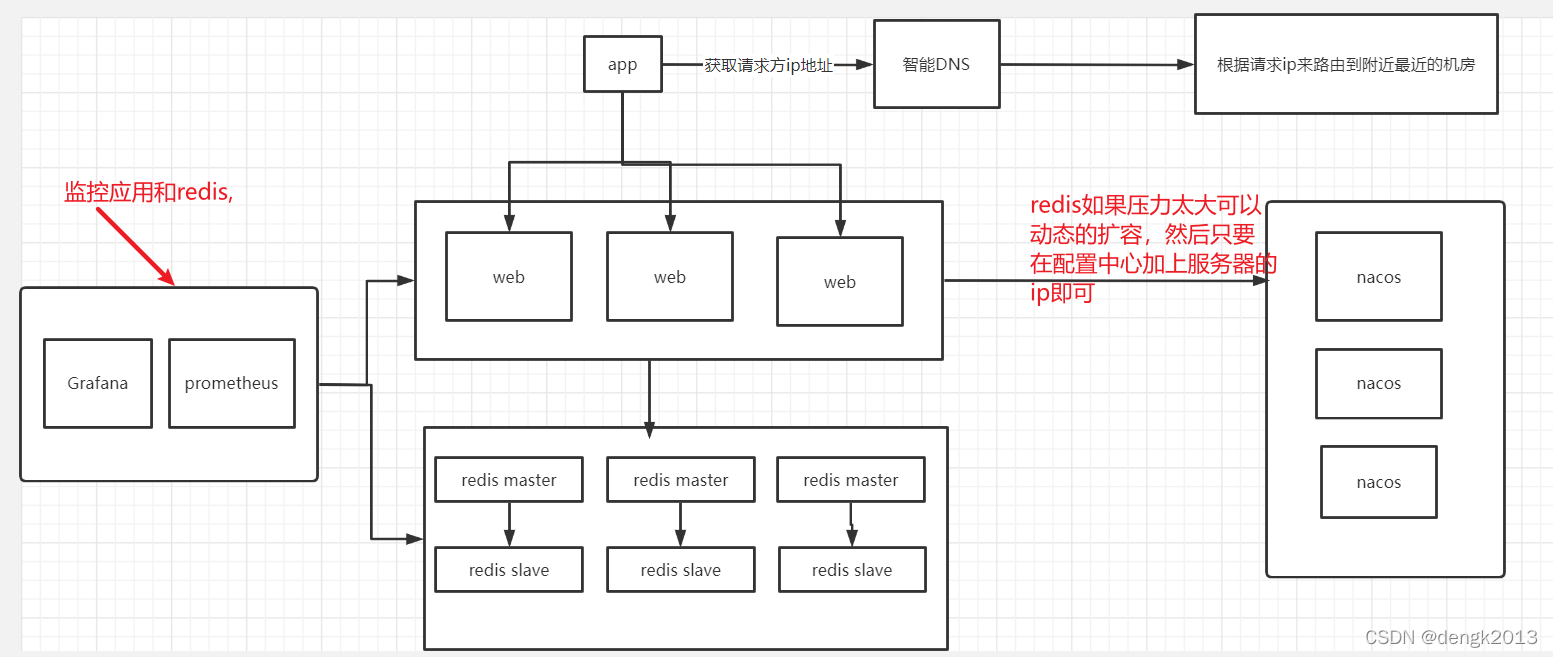
单体架构系统重新架构
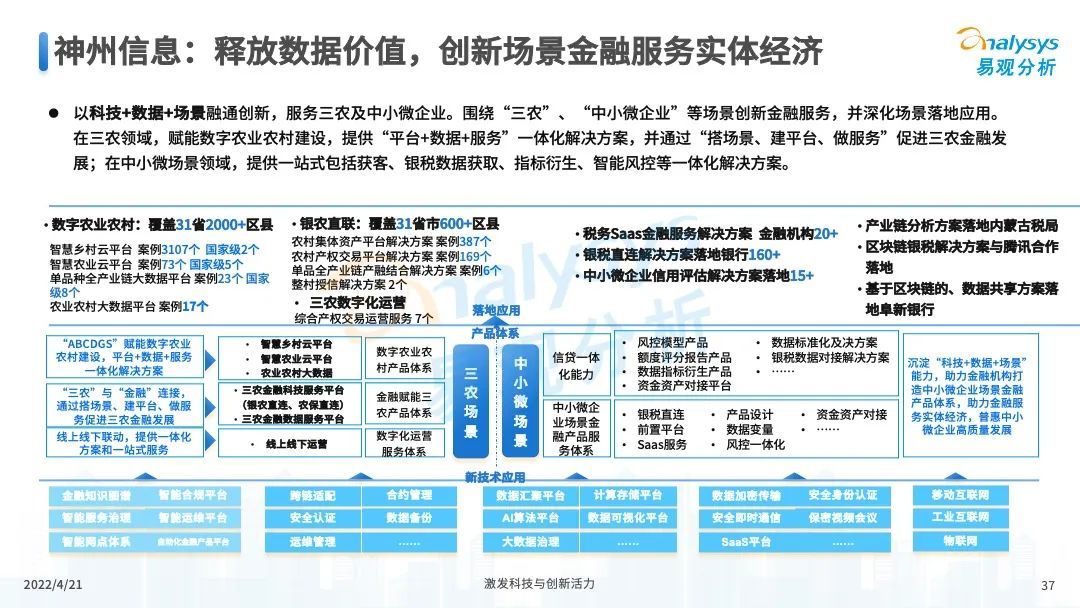
2022年中国数字科技专题分析

Large factory technology implementation | industry solution series tutorials
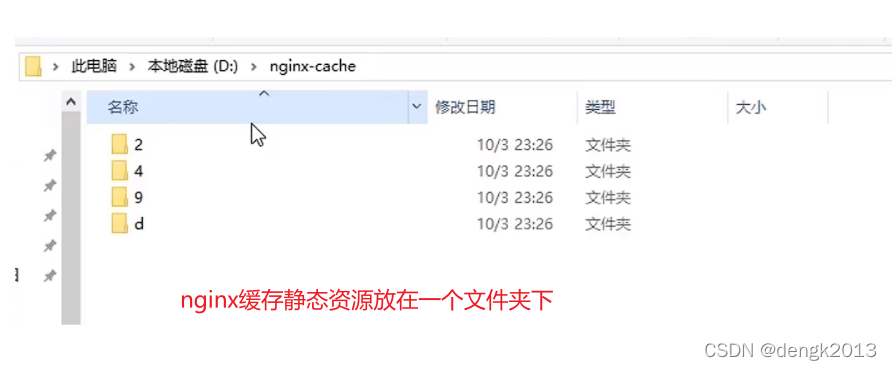
Multi level cache usage
随机推荐
电脑怎么重装系统后显示器没有信号了
APISIX jwt-auth 插件存在错误响应中泄露信息的风险公告(CVE-2022-29266)
建设星际计算网络的愿景
Explanation 2 of redis database (redis high availability, persistence and performance management)
Go concurrency and channel
Explanation of redis database (IV) master-slave replication, sentinel and cluster
WPS品牌再升级专注国内,另两款国产软件低调出国门,却遭禁令
What is CNAs certification? What are the software evaluation centers recognized by CNAs?
什么是CNAS认证?CNAS认可的软件测评中心有哪些?
Cookie&Session
Calculate the number of occurrences of a character
Upgrade MySQL 5.1 to 5.69
MetaLife与ESTV建立战略合作伙伴关系并任命其首席执行官Eric Yoon为顾问
Rsync + inotify remote synchronization
携号转网最大赢家是中国电信,为何人们嫌弃中国移动和中国联通?
通過 PDO ODBC 將 PHP 連接到 MySQL
腾讯Offer已拿,这99道算法高频面试题别漏了,80%都败在算法上
Common types of automated testing framework ▏ automated testing is handed over to software evaluation institutions
开源项目推荐:3D点云处理软件ParaView,基于Qt和VTK
Modèle de Cluster MySQL et scénario d'application