Solution to the trial of ycu Blue Bridge Cup programming competition in 2021

It may be the last time in the training team to participate in the topic ~

A： Simple check-in question

The question ：

practice ： There are two situations , Odd positions are odd and even positions are odd . Then judge by violence . Um. … I wanted to finish this problem by backhand counting odd numbers , As a result, a false check-in was sent , There is a situation 0 1 0 1 1, There is only one case of this , Just line up 1 0 1 0 1, So we have to judge the number of odd numbers to decide which one to choose .

Code ：

#include<bits/stdc++.h>
using namespace std;
const int N = 1e6+10;
int main() {
    
  int n; scanf("%d", &n);
  int x = 0, y = 0, cntj = 0;
  for(int i = 1, a; i <= n; ++i) {
    
    scanf("%d", &a); 
    if(a & 1) {
    
      ++cntj;
      if(i&1) ++x;
      else ++y;
    }
  } 
  int res;
  if(cntj * 2 == n) res = min(x, y);
  else if(cntj * 2 < n) res = x;
  else res = y;
  printf("%d\n", res);
  return 0;
} 

B： Fried chicken is simply added

The question ：

practice ： Small scale violence , Send out directly 70 branch . about 1e18 Data partition method , It is divided into 1e18 individual 1, Separate two boards , The number of schemes separated by these two boards is the answer . The first board has a total of (n+1) A place to put , The second board is based on the first board (n+2) A place to put , Divided by 2( The sequence of the first board and the second board may be repeated ). You can find the answer is $C_{n+2}^2=\frac{(n+1)(n+2)}{2}$, But the best thing is to find the law and push the formula , You have to be careful in the middle. Ow ~

Code ：

#include<bits/stdc++.h>
#define fio ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define lson rt<<1, l, mid
#define rson rt<<1|1, mid+1, r
#define PI acos(-1)
#define eps 1e-5
using namespace std;
typedef long long LL;
typedef pair<LL, int> pli;
typedef pair<int, int> pii;
typedef pair<LL, LL> pll;
typedef pair<double, double> pdd;
typedef map<char, int> mci;
typedef map<string, int> msi;
template<class T>
void read(T &res) {
    
  int f = 1; res = 0;
  char c = getchar();
  while(c < '0' || c > '9') {
     if(c == '-') f = -1; c = getchar(); }
  while(c >= '0' && c <= '9') {
     res = res * 10 + c - '0'; c = getchar(); }
  res *= f;
}
const int N = 1003;
const LL Mod = 998244353;
int main() {
    
  LL n; scanf("%lld", &n);
  LL x = n + 1, y =  n + 2;
  if(x&1) y /= 2;
  else x /= 2;
  x %= Mod; y %= Mod;
  printf("%lld\n", x * y % Mod);
  return 0;
}

C： Can't you avoid the date of the Blue Bridge Cup this time

The question ：

practice ： Direct violence .

Code ：

#include <iostream>
#include <cstdio>
#include <fstream>
#include <algorithm>
#include <cmath>
#include <deque>
#include <vector>
#include <queue>
#include <string>
#include <cstring>
#include <map>
#include <stack>
#include <set>
using namespace std;
typedef long long LL;
const int INF = 0x3f3f3f3f;
const double Pi = acos(-1);
namespace io{
    
  template <typename T> inline void read(T &x) {
    
    x = 0; T f = 1;char s = getchar();
    for(; !isdigit(s); s = getchar()) if(s == '-') f = -1;
    for(;  isdigit(s); s = getchar()) x = (x << 3) + (x << 1) + (s ^ 48);
    x *= f;
  }
  template <typename T> inline void write(T x) {
    
    if(x < 0) putchar('-'), x = -x;
    if(x > 9) write(x/10);
    putchar(x%10+'0');
  }
};
#define fio ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define _for(n,m,i) for (int i = (n); i < (m); ++i)
#define _rep(n,m,i) for (int i = (n); i <= (m); ++i)
#define _srep(n,m,i)for (int i = (n); i >= (m); i--)
#define _sfor(n,m,i)for (int i = (n); i > (m); i--)
#define ef(u, i) for(int i = head[u]; i; i = e[i].next)
#define lson rt << 1, l, mid
#define rson rt << 1 | 1, mid + 1, r
#define lowbit(x) x & (-x)
#define pii pair<int,int>
#define fi first
#define se second
int yue[] = {
    0,31,28,31,30,31,30,31,31,30,31,30,31};
int rn(int x) {
    
  return (x % 4 == 0 && x % 100 != 0) || x % 400 == 0;
}
int main() {
    
  int n = 1937, y = 1, r = 1, w = 5, ans = 0;
  while(1) {
    
    r = r % yue[y] + 1;
    if(r == 1) {
    
      y = y % 12 + 1;
      if(y == 1) n++;
      if(y == 2) {
    
        if(rn(n)) yue[2] = 29;
        else yue[2] = 28;
      }
    }
    w = w % 7 + 1;
    if(w == 1) ans++;
    if(n == 2021 && y == 3 && r == 20) break;
  }
  cout << ans << endl;
	return 0;
}

answer ：4394

D：01 maze

The question ：

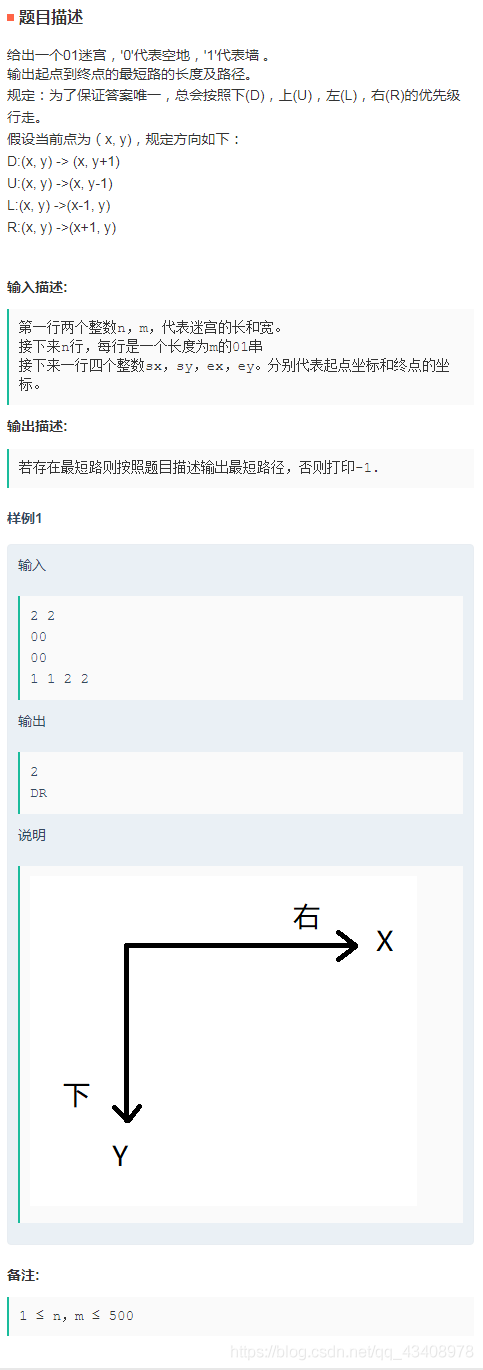
practice ：BFS Search for + Path record . Maybe the starting point or the ending point is an obstacle , So direct output -1, Maybe the beginning is the end , Output 0 And an empty string .

Code ：

#include<bits/stdc++.h>
#define fio ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define lson rt<<1, l, mid
#define rson rt<<1|1, mid+1, r
#define PI acos(-1)
#define eps 1e-5
using namespace std;
typedef long long LL;
typedef pair<LL, int> pli;
typedef pair<int, int> pii;
typedef pair<LL, LL> pll;
typedef pair<double, double> pdd;
typedef map<char, int> mci;
typedef map<string, int> msi;
template<class T>
void read(T &res) {
    
  int f = 1; res = 0;
  char c = getchar();
  while(c < '0' || c > '9') {
     if(c == '-') f = -1; c = getchar(); }
  while(c >= '0' && c <= '9') {
     res = res * 10 + c - '0'; c = getchar(); }
  res *= f;
}
const int N = 510;
const LL Mod = 998244353;
const int INF = 0x3f3f3f3f;
const int ne[4][2] = {
    0, 1, 0, -1, -1, 0, 1, 0};
string nec = "DULR";
int n, m;
char tu[N][N], pre[N][N];
int vis[N][N], dis = -INF;
int sx, sy, ex, ey, tx, ty;
struct xx {
     int x, y, step; } u;
void bfs() {
    
  if(tu[sx][sy] == '1') return;
  queue<xx> q;
  q.push(xx {
    sx, sy, 0});
  vis[sx][sy] = 1;
  while(!q.empty()) {
    
    u = q.front(); q.pop();
    if(u.x == ex && u.y == ey) {
     dis = u.step; break; }
    for(int i = 0; i < 4; ++i) {
    
      tx = u.x + ne[i][0]; ty = u.y + ne[i][1];
      if(tx > 0 && tx <= n && ty > 0 && ty <= m && !vis[tx][ty] && tu[tx][ty] == '0') {
    
        vis[tx][ty] = 1;
        q.push(xx {
    tx, ty, u.step+1});
        pre[tx][ty] = nec[i];
      }
    }
  }
}
void Print() {
     // The output path 
  if(dis == -INF) {
    
    puts("-1"); return ;
  }
  string res = "";
  tx = ex; ty = ey;
  int i;
  while(tx != sx || ty != sy) {
    
    res += pre[tx][ty];
    i = nec.find(pre[tx][ty]);
    tx -= ne[i][0]; ty -= ne[i][1];
  }
  reverse(res.begin(), res.end());
  cout << dis << "\n" << res << "\n";
}
int main() {
    
  scanf("%d %d", &n, &m);
  for(int i = 1; i <= n; ++i) scanf("%s", tu[i]+1);
  scanf("%d %d %d %d", &sx, &sy, &ex, &ey);
  memset(pre, '0', sizeof pre);
  bfs(); Print();
  return 0;
}

E： perseverance prevails

The question ：

practice ： The longest ascending subsequence template problem , There are three ways ,DP, Tree array , Two points , Can search in a small area .

Code ：

#include <algorithm>
#include <iostream>
#include <fstream>
#include <cstdlib>
#include <cstring>
#include <climits>
#include <vector>
#include <cstdio>
#include <queue>
#include <cmath>
#include <set>
#include <map>
using namespace std;
#define fio ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define _for(n,m,i) for (register int i = (n); i < (m); ++i)
#define _rep(n,m,i) for (register int i = (n); i <= (m); ++i)
#define lson rt<<1, l, mid
#define rson rt<<1|1, mid+1, r
#define PI acos(-1)
#define eps 1e-8
#define rint register int
using namespace std;
typedef long long LL;
typedef pair<LL, int> pli;
typedef pair<int, int> pii;
typedef pair<double, int> pdi;
typedef pair<LL, LL> pll;
typedef pair<double, double> pdd;
typedef map<int, int> mii;
typedef map<char, int> mci;
typedef map<string, int> msi;
template<class T>
void read(T &res) {
    
  int f = 1; res = 0;
  char c = getchar();
  while(c < '0' || c > '9') {
     if(c == '-') f = -1; c = getchar(); }
  while(c >= '0' && c <= '9') {
     res = res * 10 + c - '0'; c = getchar(); }
  res *= f;
}
const int ne[8][2] = {
    1, 0, -1, 0, 0, 1, 0, -1, -1, -1, -1, 1, 1, -1, 1, 1};
const int INF = 0x3f3f3f3f;
const int N = 3e5+10;
const LL Mod = 1e9+7;
const int M = 1e6+10;
vector<int> a;
int main() {
    
  int n; scanf("%d", &n);
  for(int i = 1, x, pos; i <= n; ++i) {
    
    scanf("%d", &x);
    pos = lower_bound(a.begin(), a.end(), x) - a.begin();
    if(pos == a.size()) a.push_back(x);
    else if(a[pos] > x) a[pos] = x;
  }
  printf("%d\n", a.size());
  return 0;
}

F：Mex

The question ：

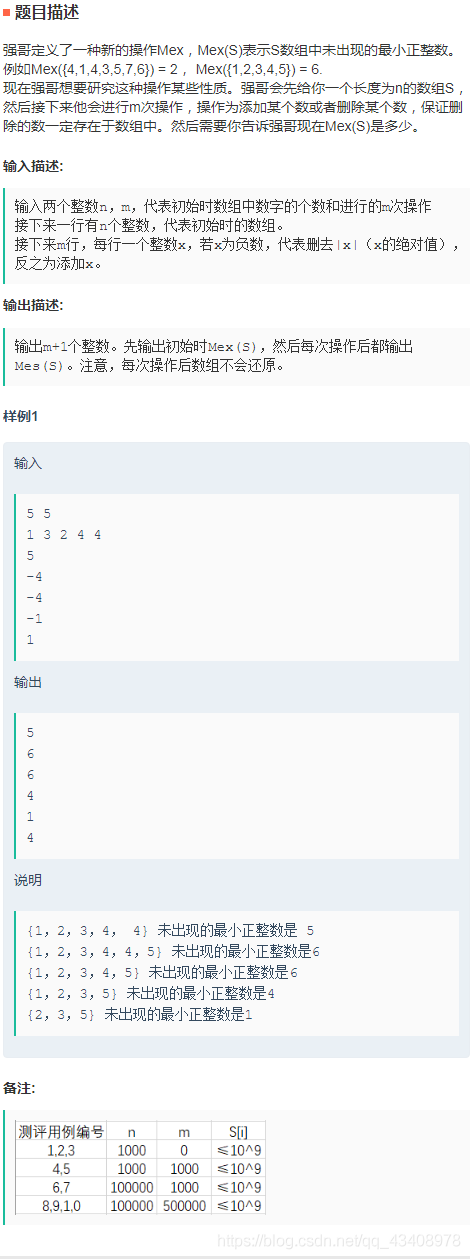
practice ： Two points answer + Tree array . First, when this number is greater than or equal to n+m when , This number will be useless , So use a bucket , That is to say ton The array records less than or equal to n+m Number of occurrences of ,ton[x] representative x How many times has it appeared . According to the idea of reverse order of tree array , Tree array is used to maintain less than or equal to x How many different numbers are there , Then the answer can be divided into the following situations ：

• Less than or equal to x-1 The different numbers are x-1 individual , So when ton[x] by 0 The answer is x.
• Less than or equal to x-1 The different numbers are x-1 individual , however ton[x] Not for 0, That is to say x（ Include ） There have been numbers before , Then the answer must be x after .
• Less than or equal to x-1 There is no difference in numbers x-1 individual , That means the answer must appear in x front .

Code ：

#include <algorithm>
#include <iostream>
#include <fstream>
#include <cstdlib>
#include <cstring>
#include <climits>
#include <vector>
#include <cstdio>
#include <queue>
#include <cmath>
#include <set>
#include <map>
using namespace std;
#define fio ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define _for(n,m,i) for (register int i = (n); i < (m); ++i)
#define _rep(n,m,i) for (register int i = (n); i <= (m); ++i)
#define lson rt<<1, l, mid
#define rson rt<<1|1, mid+1, r
#define PI acos(-1)
#define eps 1e-8
#define rint register int
typedef long long LL;
typedef pair<LL, int> pli;
typedef pair<int, int> pii;
typedef pair<double, int> pdi;
typedef pair<LL, LL> pll;
typedef pair<double, double> pdd;
typedef map<int, int> mii;
typedef map<char, int> mci;
typedef map<string, int> msi;
template<class T>
void read(T &res) {
    
  int f = 1; res = 0;
  char c = getchar();
  while(c < '0' || c > '9') {
     if(c == '-') f = -1; c = getchar(); }
  while(c >= '0' && c <= '9') {
     res = res * 10 + c - '0'; c = getchar(); }
  res *= f;
}
const int ne[8][2] = {
    1, 0, -1, 0, 0, 1, 0, -1, -1, -1, -1, 1, 1, -1, 1, 1};
const int INF = 0x3f3f3f3f;
const int N = 6e5+10;
const LL Mod = 1e9+7;
const int M = 1e6+10;
int ton[N], b[N], n;
// Tree array 
int lowbit(int x) {
     return x&(-x); }  
void Add(int p, int x) {
    
  for(; p < N; p += lowbit(p)) b[p] += x;
}
int Sum(int p) {
    
  int sum = 0;
  for(; p; p -= lowbit(p)) sum += b[p];
  return sum;
}
// Two points search 
int binary_search() {
    
  int l = 0, r = N, mid; 
  while(l <= r) {
    
    mid = l + r >> 1;
    if(Sum(mid-1) == mid-1) {
    
      if(!ton[mid]) return mid;
      else l = mid + 1; 
    } else r = mid - 1;
  }
  return N;
}
int main() {
    
  int n, m, x;
  scanf("%d %d", &n, &m);
  for(int i = 1; i <= n; ++i) {
    
    scanf("%d", &x); 
    if(x <= n + m) ++ton[x];
  }
  for(int i = 1; i < N; ++i) {
    
    if(ton[i]) Add(i, 1);
  }
  printf("%d\n", binary_search());
  while(m--) {
    
    scanf("%d", &x);
    if(x < 0) {
    
      x = -x;
      --ton[x];
      if(!ton[x]) Add(x, -1);
    } else {
    
      ++ton[x];
      if(ton[x] == 1) Add(x, 1);
    }
    printf("%d\n", binary_search());
  }
  return 0;
}

G： Regular Fibonacci

The question ：

practice ： Matrix fast power .

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 3;
const int Mod = 998244353;
LL n, m;
struct Mar {
    
  LL a[N][N];
  Mar operator * (const Mar &m) {
    
    Mar res;
    res.init();
    for(int i = 0; i < N; ++i) {
    
      for(int j = 0; j < N; ++j) {
    
        for(int k = 0; k < N; ++k) {
    
          res.a[i][j] = (res.a[i][j] + this->a[i][k] * m.a[k][j] % Mod) % Mod;
        }
      }
    }
    return res;
  }
  void init(int f = 0) {
    
    memset(a, 0, sizeof a);
    // Initialize it to the identity matrix 
    if(f == 1) {
    
      this->a[0][0] = this->a[1][1] = this->a[2][2] = 1;
    }
    // Initialize it as a construction matrix 
    if(f == 2) {
    
      this->a[0][0] = this->a[0][1] = this->a[0][2] = this->a[1][0] = this->a[2][1] = 1;
    }
    // Initialize it to include Fibonacci matrix 
    if(f == 3) {
    
      this->a[0][0] = 2;
      this->a[2][0] = this->a[1][0] = 1;
    }
  }
};
Mar ksm(Mar m, LL k) {
    
  Mar res;
  res.init(1);
  while(k) {
    
    if(k & 1) res = res * m;
    m = m * m;
    k >>= 1;
  }
  return res;
}
int main() {
    
  scanf("%lld", &n);
  Mar m1, m2;
  for(int i = 1; i <= n; ++i) {
    
    scanf("%lld", &m);
    m2.init(3);
    if(m < 3) printf("%lld\n", m2.a[2-m][0]);
    else {
    
      m1.init(2);
      printf("%lld\n", (ksm(m1, m-2)*m2).a[0][0]);
    }
  }
  return 0;
}