当前位置:网站首页>【递归之数的拆分】n分k,限定范围的拆分
【递归之数的拆分】n分k,限定范围的拆分
2022-04-23 15:32:00 【MC快乐的苦小怕】
题目自己编的
1.n分k
Ⅰ:
N拆分K项①
题目描述
问题描述
有N颗弹珠要分给K个人,给定N、K,求有多少种分配方案。
输入描述
一行,两个整数,为N、K
输出描述
一个整数,表示分配的方案数。
输入样例
7 3
输出样例
36
数据范围
1<=K<=8
K<=N<=30
提示
4个球分给三个人,有15种分配方案
0 0 4
0 1 3
0 2 2
0 3 1
0 4 0
1 0 3
1 1 2
1 2 1
1 3 0
2 0 2
2 1 1
2 2 0
3 0 1
3 1 0
4 0 0
注意:1 3 5, 1 5 3, 3 5 1算为3种方案
#include <iostream>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <string>
#include <cstring>
#include <vector>
#include <stack>
#include <list>
#include <limits.h>
using namespace std;
int cnt=0;
int n,k;
void doit(int x,int step) //x是剩下的乒乓球数量,step是当前分配到的是第几个人
{
if(step==k){
//个数到了,不能分了,该“归”了!
cnt++; //算为一种方案
return; //继续寻找方案qwq
}
for(int i=0;i<=x;i++)doit(x-i,step+1); //从每个人最少的0开始,列举每一种可行的方案,并最终得到答案
}
int main()
{
cin>>n>>k;
doit(n,1);
cout<<cnt;
//直接出结果
return 0;
}
题目描述
N个乒乓球,分成K堆,问有多少种不同的分法。
例如:n=7,k=3,下面三种划分方案被认为是相同的。
1 1 5
1 5 1
5 1 1
样例输入
7 3
样例输出
4
提示
6<N<=200
2<=K<=6
这里题目明确说明了这个是不能有那种重复的分配方法的,所以该怎么分配n?
这题其实就是一道递推的放苹果,只不过就是稍稍有一点变化。
递归解法①
int apple(int m,int n){
//纯递推思路
if(m==0||n==1) return 1;
if(n>m) return apple(m,m);
else return apple(m,n-1)+apple(m-n,n);
}
递归解法②
void apple(int pre,int n,int step){
//递归的思路
if(step==1) {
cnt++;
return;
}
for(int i=pre;i<=n/step;i++)apple(i,n-i,step-1);
}
限定范围的拆分①
题目描述
问题描述
有N颗珍珠要分给K个人,要求每个人最少为MIN颗,最多为MAX颗。给定N、K、MIN、MAX,求满足分配要求的方案数,若没有合适的方案,则输出0。
输入描述
一行,四个整数,分别表示N、K、MIN、MAX
输出描述
一个整数,表示符合分配要求的方案数。
输入样例
7 3 1 4
输出样例
12
数据范围
K<=N<=30
数据范围
1<=K<=8
K<=N<=30
注意:1, 3, 5 1, 5, 3 5, 3, 1 算为3种方案
这道题竟然限制了上和下的边界,其实我们只需要把上下边界带入问题,就很容写出来了
#include <iostream>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <string>
#include <cstring>
#include <vector>
#include <stack>
#include <list>
#include <limits.h>
using namespace std;
int cnt=0,maxn,minn;
int n,k;
void doit(int x,int step)
{
if(step==k){
if(x>=minn && x<=maxn)cnt++; //判断此方案是否合法
return; //不管合不合法还是要继续寻找新的方案
}
for(int i=minn;i<=min(maxn,x);i++)doit(x-i,step+1); //如果剩下的还不足maxn,那么只能列举到x(也就是min(maxn,x))
}
int main()
{
cin>>n>>k>>minn>>maxn;
doit(n,1);
cout<<cnt;
return 0;
}
限定范围的拆分②
题目描述
问题描述
有N个乒乓球分成K堆,要求每堆最少为MIN个,最多为MAX个。给定N、K、MIN、MAX,求满足分配要求的方案数,若没有合适的方案,则输出0。
输入描述
一行,四个整数,分别表示N、K、MIN、MAX
输出描述
一个整数,表示符合分配要求的方案数。
输入样例
7 3 1 4
输出样例
3
数据范围
K<=N<=30
数据范围
1<=K<=8
K<=N<=30
注意:1, 3, 5 1, 5, 3 5, 3, 1 算为1种方案
同样,代码上:
void doit(int x,int step,int o)
{
if(step==k){
if(x>=max(o,minn) && x<=maxn)cnt++;
return;
}
for(int i=max(o,minn);i<=min(maxn,x);i++)doit(x-i,step+1,i);
}
版权声明
本文为[MC快乐的苦小怕]所创,转载请带上原文链接,感谢
https://xiaoguogsc.blog.csdn.net/article/details/124257703
边栏推荐
- [backtrader source code analysis 18] Yahoo Py code comments and analysis (boring, interested in the code, you can refer to)
- Cookie&Session
- Mysql database explanation (10)
- 如何设计一个良好的API接口?
- PHP PDO ODBC loads files from one folder into the blob column of MySQL database and downloads the blob column to another folder
- Mysql database explanation (IX)
- 【Leetcode-每日一题】安装栅栏
- el-tree实现只显示某一级复选框且单选
- Mysql database explanation (VII)
- Connectez PHP à MySQL via aodbc
猜你喜欢
Krpano panorama vtour folder and tour
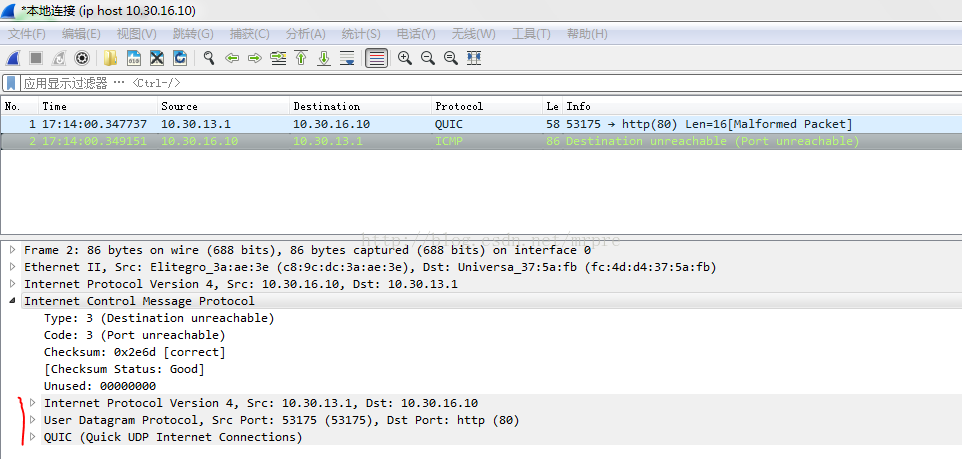
About UDP receiving ICMP port unreachable
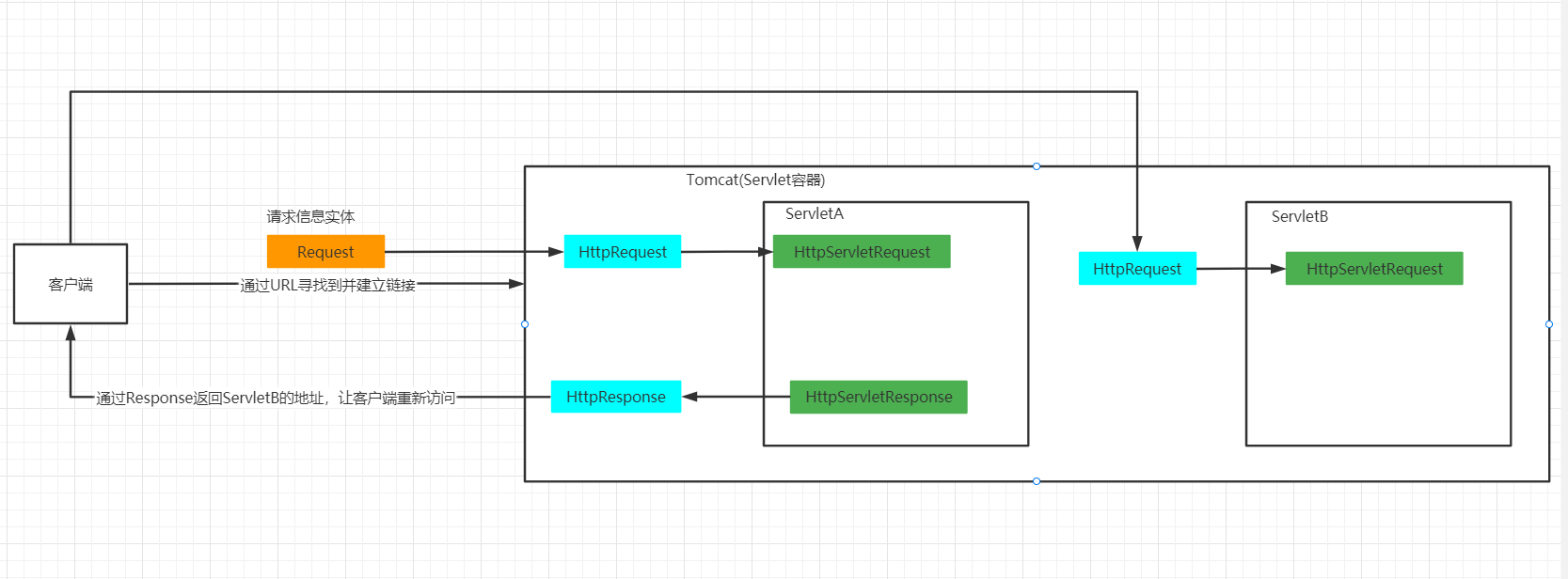
重定向和请求转发详解
今日睡眠质量记录76分
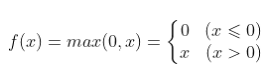
Advantages, disadvantages and selection of activation function

TLS / SSL protocol details (30) RSA, DHE, ecdhe and ecdh processes and differences in SSL
KNN, kmeans and GMM
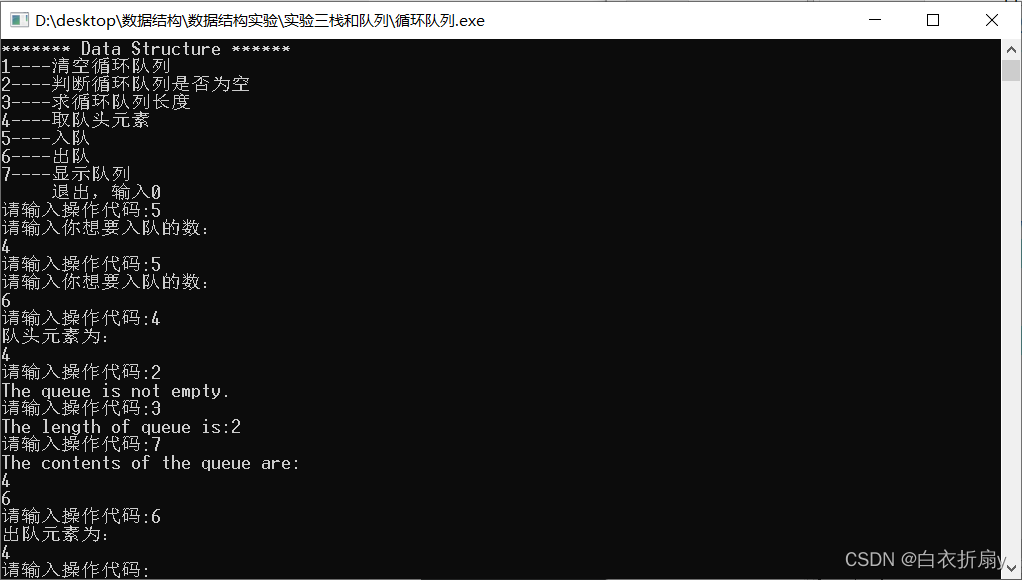
Have you learned the basic operation of circular queue?
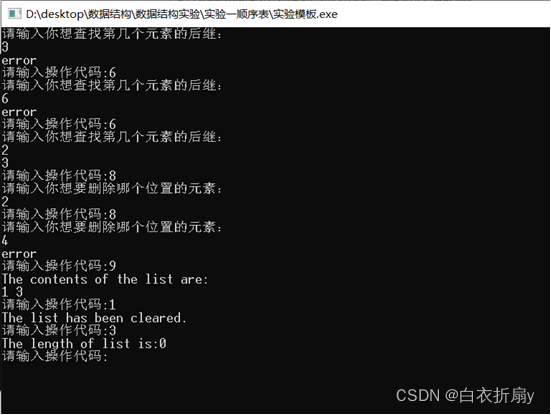
Have you really learned the operation of sequence table?
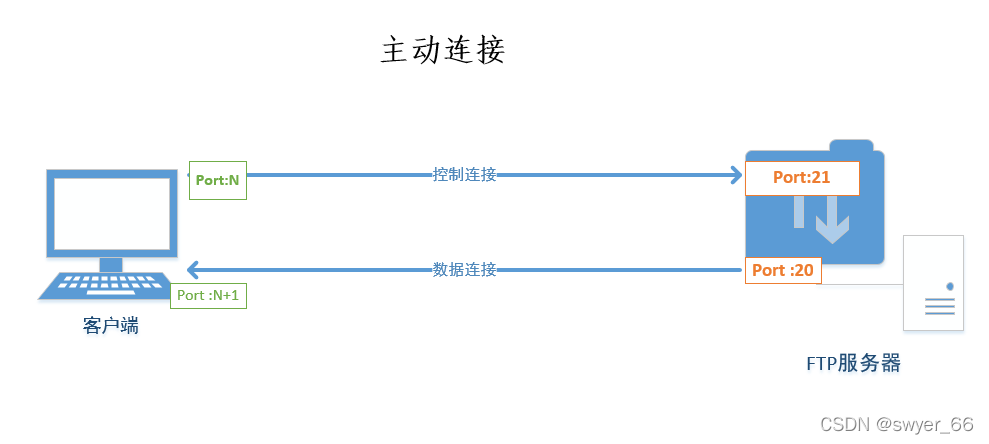
Analysis of common storage types and FTP active and passive modes
随机推荐
Leetcode学习计划之动态规划入门day3(198,213,740)
API gateway / API gateway (II) - use of Kong - load balancing
How to test mobile app?
Baidu written test 2022.4.12 + programming topic: simple integer problem
API gateway / API gateway (III) - use of Kong - current limiting rate limiting (redis)
YML references other variables
How to use OCR in 5 minutes
Independent operation smart farm Innovation Forum
Nacos程序连接MySQL8.0+ NullPointerException
SSH connects to the remote host through the springboard machine
网站某个按钮样式爬取片段
MySQL InnoDB transaction
如果conda找不到想要安装的库怎么办PackagesNotFoundError: The following packages are not available from current
Analysis of common storage types and FTP active and passive modes
el-tree实现只显示某一级复选框且单选
Tun equipment principle
函数(第一部分)
PHP PDO ODBC将一个文件夹的文件装载到MySQL数据库BLOB列,并将BLOB列下载到另一个文件夹
Tun model of flannel principle
MySQL installation process (steps for successful installation)