Principle of linear regression

1. The regression model is established according to the training data $y=w_1{x}_1+w_2{x}_2+...+w_n{x}_n+b$
2. Establish the error loss function between the predicted value and the real value
3. The gradient descent method is used to optimize the error loss function , Predict the optimal weight and offset

The example analysis

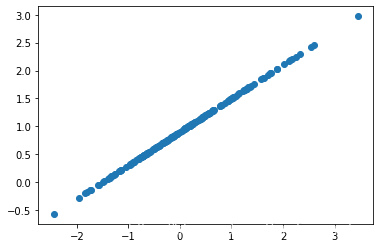
1. Training data generation

• Random generation 200 Data points subject to normal distribution
• The data itself is distributed as $y=0.6x+0.9$

The visualization code of random data points is as follows ：

import tensorflow as tf
import matplotlib.pyplot as plt
X = tf.random.normal(shape=(200, 1), mean=0, stddev=1)
y_true = tf.matmul(X, [[0.6]]) + 0.9
plt.scatter(X,y_true)
plt.show()

2. Build a linear regression model

use TensorFlow Build a linear regression model , The code is as follows ：

def Linear_regression():
	with tf.compat.v1.Session() as sess:
		#  Generate random data with normal distribution 
	    X = tf.random.normal(shape=(200, 1), mean=0, stddev=1)
	    y_true = tf.matmul(X, [[0.6]]) + 0.9
		
		#  Initialize the weight and bias of linear regression 
	    weight = tf.Variable(initial_value=tf.random.normal(shape=(1, 1)))
	    bias = tf.Variable(initial_value=tf.random.normal(shape=(1, 1)))
		
		#  The linear regression model is established by using initialization parameters 
	    y_predict = tf.matmul(X, weight) + bias
	
		#  Establish the error loss function 
	    error = tf.reduce_mean(tf.square(y_predict - y_true))
	
		#  The random gradient descent method is used for model training 
	    optimizer = tf.compat.v1.train.GradientDescentOptimizer(learning_rate=0.05).minimize(error)
	
		#  Initialize variables in the session 
	    init = tf.compat.v1.global_variables_initializer()
	    sess.run(init)
	    
	    #  Record the loss value obtained in each training 
	    error_set = [] 
	    
	    #  Training 200 Time , Print weights for each workout 、 Offset and loss 
	    for i in range(200):
	        sess.run(optimizer)
	        error_set.append(error.eval())
	        print(" The first %d The error of step is %f, The weight of %f, The offset is %f" %(i,error.eval(),weight.eval(),bias.eval()))

The operation results are as follows ：

 The first 0 The error of step is 0.869870, The weight of 1.532328, The offset is 0.675902
 The first 1 The error of step is 0.663277, The weight of 1.428975, The offset is 0.691342
 The first 2 The error of step is 0.637269, The weight of 1.346699, The offset is 0.713041
 The first 3 The error of step is 0.434829, The weight of 1.280713, The offset is 0.727712
 The first 4 The error of step is 0.456109, The weight of 1.209046, The offset is 0.745070
 The first 5 The error of step is 0.276588, The weight of 1.146608, The offset is 0.758473
 The first 6 The error of step is 0.268131, The weight of 1.080588, The offset is 0.770594
 The first 7 The error of step is 0.201195, The weight of 1.024212, The offset is 0.794897
 The first 8 The error of step is 0.136823, The weight of 0.988268, The offset is 0.804994
 The first 9 The error of step is 0.123242, The weight of 0.950725, The offset is 0.811171
 The first 10 The error of step is 0.131416, The weight of 0.922447, The offset is 0.819484
 The first 11 The error of step is 0.084628, The weight of 0.897494, The offset is 0.826534
 The first 12 The error of step is 0.072482, The weight of 0.873246, The offset is 0.833084
 The first 13 The error of step is 0.073851, The weight of 0.841141, The offset is 0.842617
 The first 14 The error of step is 0.046367, The weight of 0.811977, The offset is 0.849992
 The first 15 The error of step is 0.034317, The weight of 0.789964, The offset is 0.855224
 The first 16 The error of step is 0.026889, The weight of 0.767914, The offset is 0.861630
 The first 17 The error of step is 0.020377, The weight of 0.751666, The offset is 0.866115
 The first 18 The error of step is 0.020895, The weight of 0.735054, The offset is 0.871480
 The first 19 The error of step is 0.016006, The weight of 0.718687, The offset is 0.872991
 The first 20 The error of step is 0.012947, The weight of 0.707634, The offset is 0.875760
 The first 21 The error of step is 0.011159, The weight of 0.698776, The offset is 0.878277
 The first 22 The error of step is 0.008542, The weight of 0.688199, The offset is 0.881770
 The first 23 The error of step is 0.006672, The weight of 0.679353, The offset is 0.884191
 The first 24 The error of step is 0.005545, The weight of 0.671653, The offset is 0.885150
 The first 25 The error of step is 0.003817, The weight of 0.664658, The offset is 0.885894
 The first 26 The error of step is 0.003786, The weight of 0.658720, The offset is 0.886094
 The first 27 The error of step is 0.002937, The weight of 0.652663, The offset is 0.887146
 The first 28 The error of step is 0.002135, The weight of 0.646956, The offset is 0.888744
 The first 29 The error of step is 0.001883, The weight of 0.641135, The offset is 0.890537
 The first 30 The error of step is 0.001530, The weight of 0.637612, The offset is 0.891546
 The first 31 The error of step is 0.001205, The weight of 0.633786, The offset is 0.892773
 The first 32 The error of step is 0.000896, The weight of 0.630734, The offset is 0.892999
 The first 33 The error of step is 0.000742, The weight of 0.627161, The offset is 0.893859
 The first 34 The error of step is 0.000600, The weight of 0.624422, The offset is 0.894859
 The first 35 The error of step is 0.000556, The weight of 0.622399, The offset is 0.895277
 The first 36 The error of step is 0.000471, The weight of 0.620324, The offset is 0.895607
 The first 37 The error of step is 0.000341, The weight of 0.618261, The offset is 0.895853
 The first 38 The error of step is 0.000309, The weight of 0.616247, The offset is 0.896142
 The first 39 The error of step is 0.000233, The weight of 0.614667, The offset is 0.896652
 The first 40 The error of step is 0.000219, The weight of 0.613210, The offset is 0.896935

...
 The first 194 The error of step is 0.000000, The weight of 0.600000, The offset is 0.900000
 The first 195 The error of step is 0.000000, The weight of 0.600000, The offset is 0.900000
 The first 196 The error of step is 0.000000, The weight of 0.600000, The offset is 0.900000
 The first 197 The error of step is 0.000000, The weight of 0.600000, The offset is 0.900000
 The first 198 The error of step is 0.000000, The weight of 0.600000, The offset is 0.900000
 The first 199 The error of step is 0.000000, The weight of 0.600000, The offset is 0.900000

The broken line diagram of loss value change during training is as follows ：

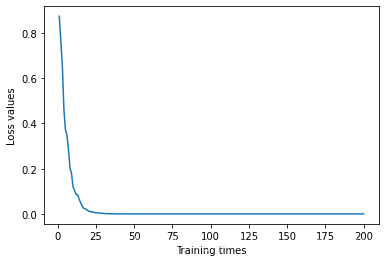
You can see that as the number of training increases , The value of the loss function decreases gradually , Finally, it becomes 0. The optimal parameters predicted in the training process are also consistent with the actual data distribution parameters .

Summary

This paper introduces the basic principle and steps of linear regression , And based on TensorFlow A simple linear regression task is realized , Good results have been achieved .