当前位置：网站首页>卡尔曼滤波与惯性组合导航

卡尔曼滤波与惯性组合导航

2022-04-23 05:44:00 【＃self-discipline＃】

目录

几种最优估计

估计

最小二乘估计

估计指标

估计结果

性质

加权最小二乘估计

估计指标

估计结果

马尔柯夫估计

递推最小二乘估计

递推最小二乘估计更新公式

 

最小方差估计

估计指标

估计结果

性质

极大验后估计

几种最优估计

估计

根据测量出的状态量X的测量值Z=HX+V得到对X的估计值\widehat{X}

最小二乘估计

估计指标

J(\widehat{X})=(Z-H\widehat{X})^T(Z-H\widehat{X})=min

估计结果

由对估计指标求导得零点，知

\widehat{X}=(H^TH)^{-1}H^TZ

性质

①最小二乘估计是无偏估计，即有E(\widehat{X})=X

②最小二乘估计的均方误差阵E(\widetilde{X}\widetilde{X}^T)=(H^TH)^{-1}H^TRH(H^TH)^{-1},其中估计误差\widetilde{X}=X-\widehat{X}，测量误差的方差R=E(VV^T)

加权最小二乘估计

最小二乘估计不分差别地使用多个量测值使其符合估计指标最后得到估计值，这样常常让估计的准确性被量测性能较差的量测值影响，使得估计效果比只使用量测性能好的量测值进行估计来得低。

加权最小二乘估计使精度高的量测权重大些，精度低的量测权重小些，得到的估计比只使用精度高的量测得到的估计均方误差更小，效果更好。

估计指标

J(\widehat{X})=(Z-H\widehat{X})^TW(Z-H\widehat{X})=min,W为加权矩阵

估计结果

\widehat{X}=(H^TWH)^{-1}H^TWZ

E(\widetilde{X}\widetilde{X}^T)=(H^TWH)^{-1}H^TWRWH(H^TWH)^{-1}，

马尔柯夫估计

令W=R^{-1}得到的加权最小二乘估计称为马尔柯夫估计，通过证明可以知道马尔柯夫估计是加权最小二乘估计的最优估计

估计结果：\widehat{X}=(H^TR^{-1}H)^{-1}H^TR^{-1}Z;E(\widetilde{X}\widetilde{X}^T)=(H^TR^{-1}H)^{-1}

递推最小二乘估计

前面的最小二乘估计都是在得到所有量测之后通过构造指标方程得到估计。如果在实际中，随着时间的推移，量测不断增加，量测数值十分庞大，对计算机造成很大的资源浪费，所以需要可以随着新量测的加入对估计进行更新的递推最小二乘估计。

递推最小二乘估计更新公式

\widehat{X}_{k+1}=\widehat{X}_k+P_{k+1}H^T_{k+1}W_{k+1}(Z_{k+1}-H_{k+1}\widehat{X}_k)

P_{k+1}=P_k-P_kH^T_{k+1}(W^{-1}_{k+1}+H_{k+1}P_kH^T_{k+1})^{-1}H_{k+1}P_k

初值X_0,P_0可以任意选取，开始阶段误差跳动将很剧烈，随着量测不断更新，误差逐渐趋于稳定

最小方差估计

估计指标

J=E_{X,Z}\left \{ \right.[X-\widehat{X}(Z)]^T[X-\widehat{X}(Z)]\left. \right \}=min

估计结果

\widehat{X}_{MV}=E[X/Z]

性质

①最小方差估计的无偏性：E(\widehat{X})=X

极大验后估计

估计指标

p(x/z)=max,在z确定的情况下，确定估计\widehat{x}使得该条件概率达到最大值

贝叶斯估计

估计指标

B(\widetilde{X})=E[L(\widetilde{X})]=min;

L(\widetilde{X})满足：

贝叶斯估计和其它估计的转化

当L(\widetilde{X})=\widetilde{X}^T\widetilde{X}时，贝叶斯估计与 最小方差估计等效；

当

，贝叶斯估计与极大后验估计等效。

极大似然估计

估计指标

p(z/x)=min;在量测z确定的情况下，估计\widehat{x}使得该条件概率取最大值

线性最小方差估计

令\widehat{X}_L=A^0Z+b^0在估计是量测Z的线性函数条件下使其满足最小方差估计指标J=E_{X,Z}\left \{ \right.[X-\widehat{X}(Z)]^T[X-\widehat{X}(Z)]\left. \right \}=min

估计结果

\widehat{X}_L(Z)=m_X+C_{XZ}C^{-1}_Z(Z-m_Z)

P=E\{[X-\widehat{X}_L(Z)][X-\widehat{X}_L(Z)]^T\}=C_X-C_{XZ}C_Z^{-1}C_{ZX}

其中

m_X=E(X),C_{XZ}=E[(X-m_X)(Z-m_Z)^T]=C_XH^T,m_Z=Hm_X,C_Z=E[(Z-m_Z)(Z-m_Z)^T]=HC_XH^T+C_V; ,C_{ZX}=C_{XZ}^T=HC_X

 Var(V)=C_V,Var(X)=C_X

性质

①无偏性：E(\widehat{X})=X

记E^*[X/Z]为在量测为Z下的估计\widehat{X}_L，有

②线性1：E^*[(FX+e)/Z]=FE^*[X/Z]+e

③线性2：E^*[X/Y,M]=E^*[X/Y]+E^*[X/M]-EX,其中Z=\begin{bmatrix} Y\\M \end{bmatrix}

卡尔曼滤波

卡尔曼滤波的优点

离散型卡尔曼滤波

卡尔曼滤波基本方程

状态方程：X_k=\Phi_{k,k-1}X_{k-1}+\Gamma _{k-1}W_{k-1}

\Phi_{k,k-1}为t_{k-1}\rightarrow t_k的一步转移阵；\Gamma _{k-1}为系统噪声驱动阵；W_{k-1}为系统激励噪声序列

量测方程：Z_k=H_kX_k+V_k

H_k为量测阵，V_k为量测噪声序列

W_{k-1},V_k都是零均值的高斯白噪声向量序列(服从正态分布),且二者不相关，即两噪声满足下列噪声条件：

离散卡尔曼滤波全套算法基本公式

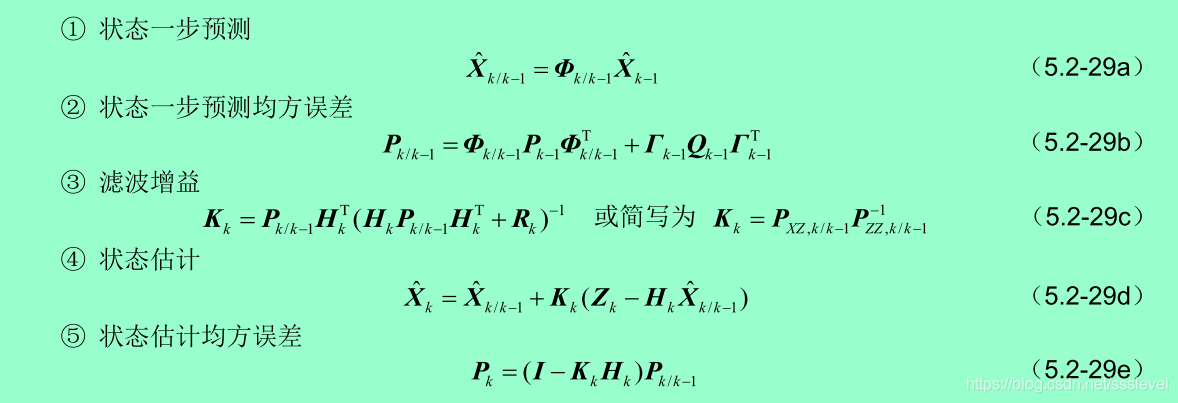
①通过状态方程进行从k-1时刻到k时刻的预测，此时的估计是基于过去的量测信息进行的，对k时刻的量测没有利用，属于先验估计，准确度较低。

②是在一步预测下得到的均方误差,其大小代表了估计的精度

③滤波增益是使用k时刻的量测对①中的估计进行修正的系数

④状态估计使用更新后的量测信息对①的估计进行修正，得到的是后验估计，准确度高

⑤是在状态估计下得到的均方误差，表征估计的精度

④，⑤就是得到的离散型卡尔曼估计的更新

 

 

 

 

 

 

 

 

版权声明
本文为[＃self-discipline＃]所创，转载请带上原文链接，感谢
https://blog.csdn.net/ssslevel/article/details/109476395

边栏推荐

猜你喜欢

随机推荐